文档内容
专题 5.5 三角恒等变换
(一)两角和与差的正弦、余弦、正切公式
1.C :cos(α-β)=cosαcosβ+sinαsinβ;
(α-β)
C :cos(α+β)=cosαcos_β-sin_αsinβ;
(α+β)
S :sin(α+β)=sinαcosβ+cosαsinβ;
(α+β)
S :sin(α-β)=sin_αcos_β-cosαsinβ;
(α-β)
T :tan(α+β)=;
(α+β)
T :tan(α-β)=.
(α-β)
2.变形公式:
tan α±tan β=tan(α±β)(1 tanαtanβ);
sincos 2sin(∓ )
4
.
sinαsinβ+cos(α+β)=cosαcosβ,
cosαsinβ+sin(α-β)=sinαcosβ,
3.辅助角公式:
函数f(α)=acos α+bsin α(a,b为常数),可以化为f(α)=sin(α+φ)或f(α)=cos(α-φ),
其中φ可由a,b的值唯一确定.
(二)二倍角的正弦、余弦、正切公式
1.S :sin 2α=2sinαcosα;
2α
C :cos 2α=cos2α-sin2α=2cos2α-1=1-2sin2α;
2α
T :tan 2α=.
2α
2.变形公式:
(1)降幂公式:cos2α=,sin2α=,sin αcos α=sin 2α.
(2)升幂公式
1+cos α=2cos2;
1-cos α=2sin2;
1+sin α=;
1-sin α=.
(3)配方变形:1+sin 2α=(sin α+cos α)2,1-sin 2α=(sin α-cos α)2
1±sinα=2,1+cosα=2cos2,1-cosα=2sin2
(4)sin 2α==;
cos 2α==.
试卷第1页,共3页
学科网(北京)股份有限公司tan ==.
(三)常见变换规律
(1)角的变换:明确各个角之间的关系(包括非特殊角与特殊角、已知角与未知角),熟
悉角的变换技巧,及半角与倍角的相互转化,如:2α=(α+β)+(α-β),α=(α+β)-β
=(α-β)+β,40°=60°-20°,+=,=2×等.
(2)名的变换:明确各个三角函数名称之间的联系,常常用到同角关系、诱导公式,把
正弦、余弦化为正切,或者把正切化为正弦、余弦.
一、单选题
1. 等于( )
A. B.1 C.0 D.
【来源】陕西省西安市莲湖区2021-2022学年高一下学期期末数学试题
【答案】C
【解析】由两角和的余弦公式得:
故选:C
2.已知 ,且 ,则 的值为( )
A. B. C. D.
【来源】辽宁省沈阳市第一中学2021-2022学年高一下学期第三次阶段数学试题
【答案】D
【解析】:因为 ,所以 ,
所以 ,又 ,
试卷第2页,共3页
学科网(北京)股份有限公司所以 .
故选:D
3.已知 均为锐角,且 ,则 ( )
A. B. C. D.
【来源】辽宁省县级重点高中协作体2021-2022学年高一下学期期末考试数学试题
【答案】A
【解析】:因为 ,
所有 ,则 ,
又 均为锐角,所以 ,所以 ,
所以 ,
所以 .故选:A.
4.已知 , ,则 的值为( )
A.2 B. C. D.
【来源】内蒙古自治区包头市2021-2022学年高一下学期期末数学试题
【答案】B
【解析】 ,解得 ,
试卷第3页,共3页
学科网(北京)股份有限公司所以 .
故选:B
5.已知 ,则 ( )
A. B. C.± D.±
【来源】陕西省汉中市六校联考2021-2022学年高一下学期期末数学试题(B卷)
【答案】D
【解析】 ,则 ,即 ,
故 ,所以 ,故 ,
所以
故选:D
6.下面公式正确的是( )
A. B.
C. D.
【来源】陕西省宝鸡市渭滨区2021-2022学年高一下学期期末数学试题
【答案】D
【解析】
试卷第4页,共3页
学科网(北京)股份有限公司对A, ,故A错误;
对B, ,故B错误;
对C, ,故C错误;
对D, ,故D正确;故选:D
7.已知 , ,则 的值为( )
A. B. C. D.
【来源】内蒙古自治区呼伦贝尔市满洲里市第一中学2021-2022学年高一下学期期末
数学试题
【答案】B
【解析】:因为 , ,
所以
.故选:B
8.设 , , ,则a,b,c大小关
系正确的是( )
A. B.
C. D.
【来源】湖北省云学新高考联盟学校2021-2022学年高一下学期5月联考数学试题
【答案】C
【解析】 ,
试卷第5页,共3页
学科网(北京)股份有限公司,
,
因为函数 在 上是增函数,
故 ,即 .故选:C.
9.已知 ,则 ( )
A. B. C. D.
【来源】海南省海口市第一中学2021-2022学年高一下学期期中考试数学试题(A)
【答案】B
【解析】:因为 ,所以
故选:B
10.若 ,则 ( )
A. B. C. D.
【来源】北京市房山区2021—2022学年高一下学期期末学业水平调研数学试题
【答案】D
试卷第6页,共3页
学科网(北京)股份有限公司【解析】:因为 ,
所以 .故选:D.
11.已知 ,则 ( )
A. B. C. D.
【来源】四川省内江市2021-2022学年高一下学期期末数学理科试题
【答案】B
【解析】:因为 ,
即 ,
即
即 ,即 ,所以
,
所以
.故选:B
12.已知 , 是第三象限角,则 =( )
试卷第7页,共3页
学科网(北京)股份有限公司A. B. C. D.
【来源】西藏林芝市第二高级中学2021-2022学年高一下学期第二学段考试(期末)
数学试题
【答案】A
【解析】由 , ,可得
由 是第三象限角,可得
则
故选:A
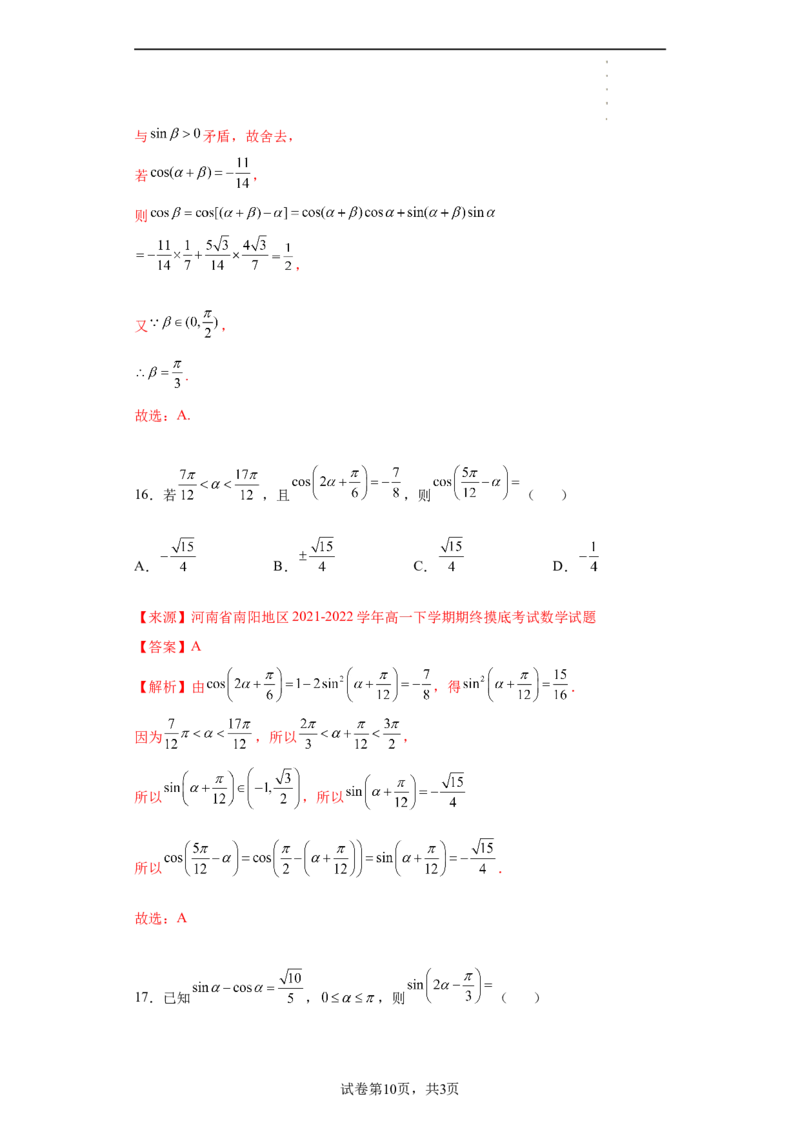
13.若 , ,且 , ,则 的值是
( )
A. B. C. 或 D. 或
【答案】B
【解析】 ,又∵ ,
∴ .
又∵ ,∴ ,
于是
,易得 ,则 .
试卷第8页,共3页
学科网(北京)股份有限公司故选:B.
14. ( )
A. B. C. D.
【来源】安徽省宣城市泾县中学2021-2022学年高一下学期第一次月考数学试题
【答案】D
【解析】原式
.故选:D.
15.若 ,则角 的值为( )
A. B. C. D.
【来源】陕西省西安中学2021-2022学年高一下学期期中数学试题
【答案】A
【解析】∵ ,
,
由 , ,得 , ,
若 ,
则
,
试卷第9页,共3页
学科网(北京)股份有限公司与 矛盾,故舍去,
若 ,
则
,
又 ,
.
故选:A.
16.若 ,且 ,则 ( )
A. B. C. D.
【来源】河南省南阳地区2021-2022学年高一下学期期终摸底考试数学试题
【答案】A
【解析】由 ,得 .
因为 ,所以 ,
所以 ,所以
所以 .
故选:A
17.已知 , ,则 ( )
试卷第10页,共3页
学科网(北京)股份有限公司A. B. C. D.
【来源】湖北省新高考联考协作体2021-2022学年高一下学期期末数学试题
【答案】D
【解析】:因为 ,所以 ,
即 ,即 ,所以 ,
又 ,
即 ,
因为 ,所以 ,
所以 ,即 ,
所以 ,所以 ,
所以
;
故选:D
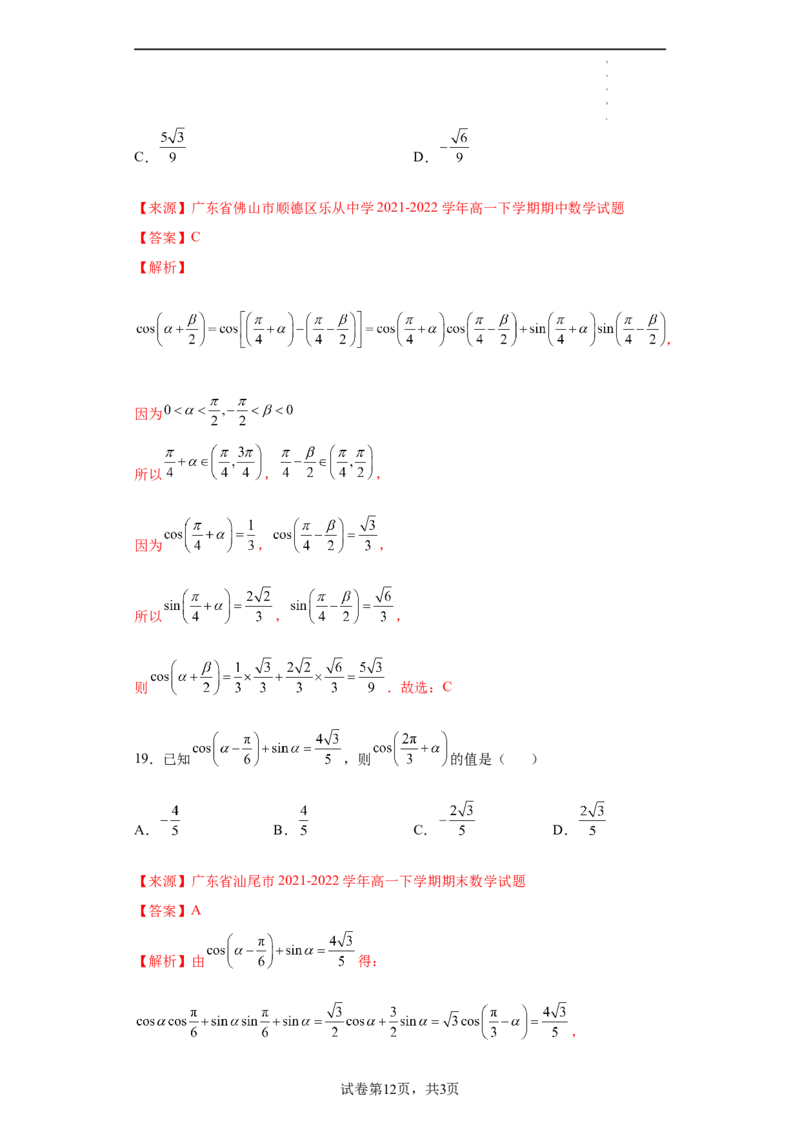
18.若 ,则
( )
A. B.
试卷第11页,共3页
学科网(北京)股份有限公司C. D.
【来源】广东省佛山市顺德区乐从中学2021-2022学年高一下学期期中数学试题
【答案】C
【解析】
,
因为
所以 , ,
因为 , ,
所以 , ,
则 .故选:C
19.已知 ,则 的值是( )
A. B. C. D.
【来源】广东省汕尾市2021-2022学年高一下学期期末数学试题
【答案】A
【解析】由 得:
,
试卷第12页,共3页
学科网(北京)股份有限公司所以, ,
所以, .
故选:A.
20.已知 ,且 ,则 ( )
A. B. C. D.
【来源】陕西省商洛市2021-2022学年高一下学期期末数学试题
【答案】C
【解析】因为 ,所以 .
又 ,
所以 ,
故选:C.
二、多选题
21.对于函数 ,下列结论正确的是( )
A. 的最小正周期为 B. 的最小值为
C. 的图象关于直线 对称 D. 在区间 上单调递增
试卷第13页,共3页
学科网(北京)股份有限公司【来源】湖北省部分普通高中联合体2021-2022学年高一下学期期中联考数学试题
【答案】AB
【解析】 ,
,A正确;
最小值是 ,B正确;
,C错误;
时, , 时, 得最小值 ,因此函数不
单调,D错误,故选:AB.
22.下列各式中,值为 的是( )
A. B.
C. D.
【来源】江西省南昌市第十中学2021-2022学年高一下学期期中考试数学试题
【答案】ABC
【解析】A: ,符合;
B: ,符合;
C: ,符合;
D: ,不符合.
故选:ABC
23.已知函数 ,则下列结论正确的有( )
A. 的最小正周期为
试卷第14页,共3页
学科网(北京)股份有限公司B.直线 是 图象的一条对称轴
C. 在 上单调递增
D.若 在区间 上的最大值为 ,则
【来源】江苏省南京师范大学附属中学2021-2022学年高一下学期期中数学试题
【答案】BD
【解析】: ,
所以 的最小正周期为 故A不正确;
因为 ,所以直线 是 图象的一条对称轴,故B正确;
当 时, ,而函数 在 上不单调,故 不正确;
当 时, ,
因为 在区间 上的最大值为 ,即 ,
所以 ,所以 ,解得 ,故D正确.
故选:BD.
24.已知函数 的周期为 ,当 时,
的( )
A.最小值为 B.最大值为 C.零点为 D.增区间为
【来源】江苏省徐州市2021-2022学年高一下学期期中数学试题
试卷第15页,共3页
学科网(北京)股份有限公司【答案】BCD
【解析】
,
因为 的周期为 ,所以 ,得 ,
所以 ,
当 时, ,所以 ,所以
,所以 的最小值为 ,最大值为2,所以A错误,B正确,
由 , ,得 ,解得 ,所以
的零点为 ,所以C正确,
由 ,得 ,所以 的增区间为 ,所以D正确,
故选:BCD
25.关于函数 ,下列命题正确的是( )
A.若 , 满足 ,则 成立;
B. 在区间 上单调递增;
试卷第16页,共3页
学科网(北京)股份有限公司C.函数 的图象关于点 成中心对称;
D.将函数 的图象向左平移 个单位后将与 的图象重合.
【来源】广东省佛山市顺德区第一中学2021-2022学年高一下学期期中数学试题
【答案】ACD
【解析】
,
对于A,若 , 满足 ,则
成立,故A正确;
对于B,由 ,得: ,即
在区间 上单调递增,故B错误;
对于C,因为 ,所以函数 的图象关于点 成中
心对称,故C正确;
对于D,将函数 的图象向左平移 个单位后得到
,其图象与 的
图象重合,故D正确.
故选:ACD
试卷第17页,共3页
学科网(北京)股份有限公司三、解答题
26.求下列各式的值
(1)
(2)
(3)
(4)
【来源】黑龙江省鸡西市第四中学2021-2022学年高一上学期期末考试数学试题
【答案】(1)0;(2) ;(3) ;(4) .
【解析】(1) .
(2)
.
(3) .
(4) .
27.已知 ,其中 .
(1)求 ;
(2)若 ,求 的值.
【来源】广东省珠海市2021-2022学年高一下学期期末数学试题(A组)
试卷第18页,共3页
学科网(北京)股份有限公司【答案】(1) (2)
【解析】(1)由 可得 ,因为 ,故 ,进
而
(2) ,故 ;
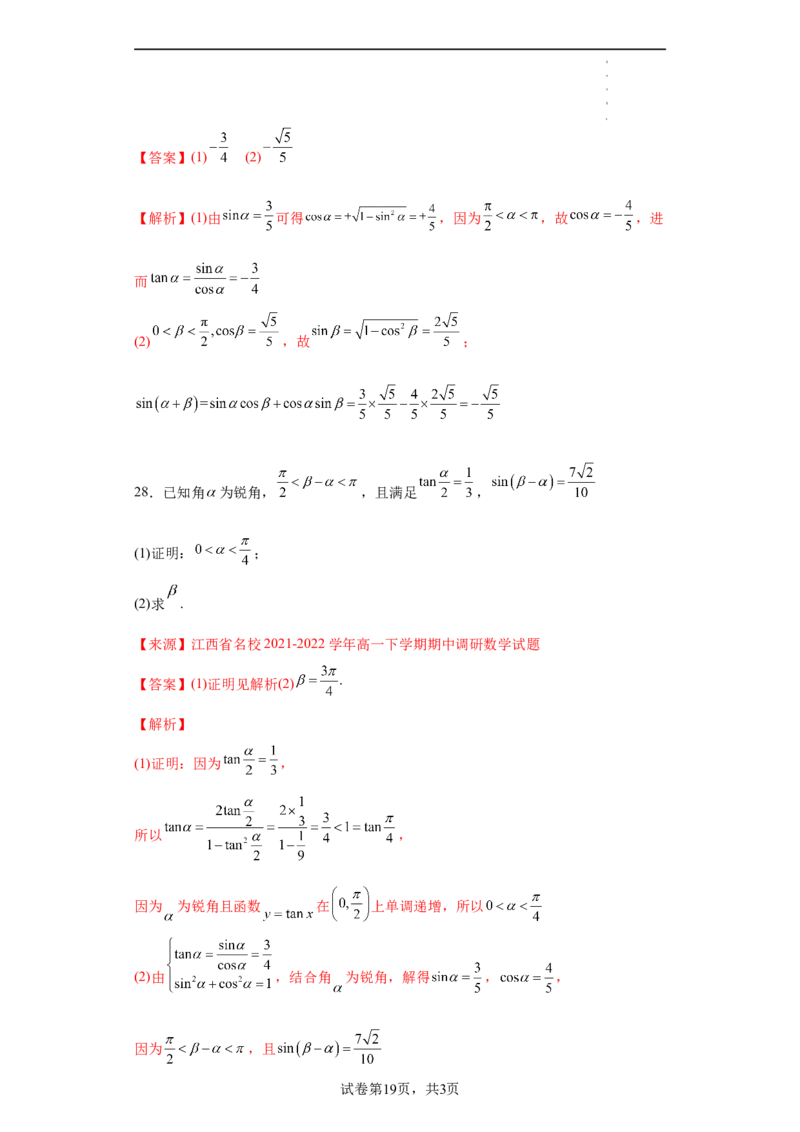
28.已知角 为锐角, ,且满足 ,
(1)证明: ;
(2)求 .
【来源】江西省名校2021-2022学年高一下学期期中调研数学试题
【答案】(1)证明见解析(2)
【解析】
(1)证明:因为 ,
所以 ,
因为 为锐角且函数 在 上单调递增,所以
(2)由 ,结合角 为锐角,解得 , ,
因为 ,且
试卷第19页,共3页
学科网(北京)股份有限公司所以 .
又 ,
所以
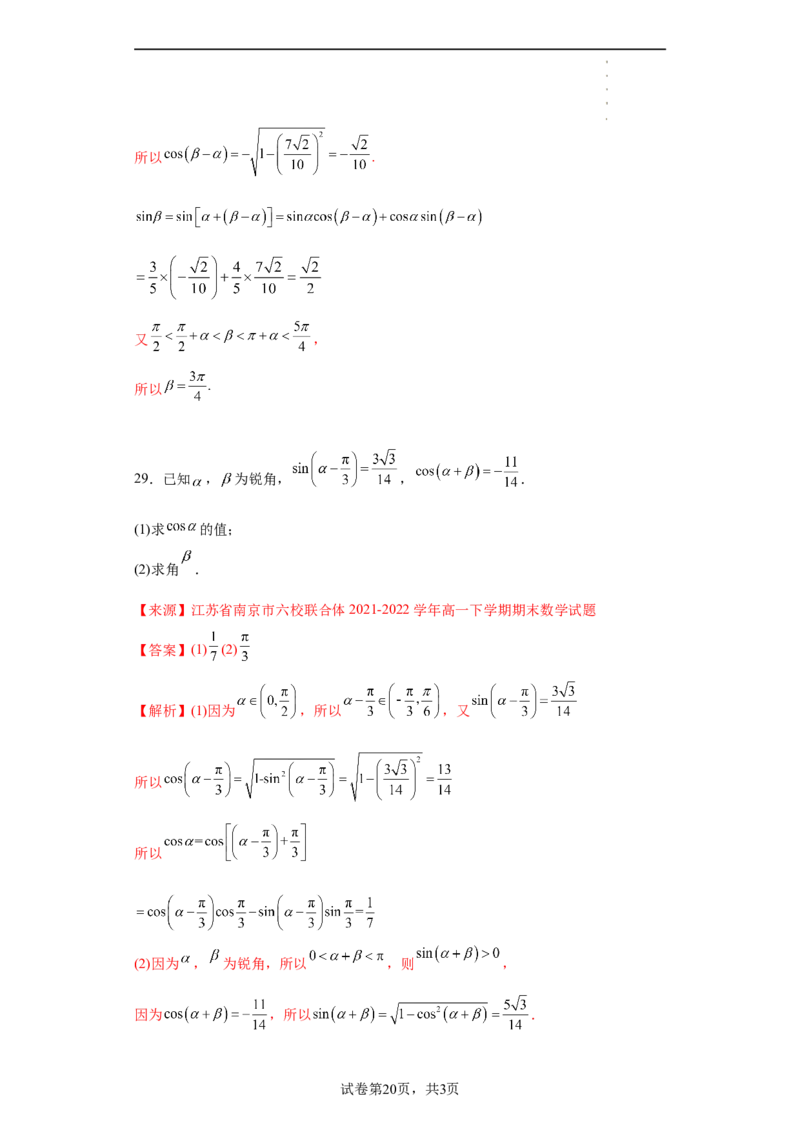
29.已知 , 为锐角, , .
(1)求 的值;
(2)求角 .
【来源】江苏省南京市六校联合体2021-2022学年高一下学期期末数学试题
【答案】(1) (2)
【解析】(1)因为 ,所以 ,又
所以
所以
(2)因为 , 为锐角,所以 ,则 ,
因为 ,所以 .
试卷第20页,共3页
学科网(北京)股份有限公司又 为锐角, ,所以 ,
故
,
因为 为锐角,所以 .
30.已知
(1)求 的值;
(2)若 都是锐角, ,求 的值.
【来源】湖北省部分市州2021-2022学年高一下学期7月期末联考数学试题
【答案】(1) (2)
【解析】(1)解: ,
.
(2)因为 都是锐角,所以 , ,
,
31.已知 是方程 的两根,求下列各式的值:
(1)
试卷第21页,共3页
学科网(北京)股份有限公司(2) ;
(3) .
【来源】江苏省泰州市兴化市楚水实验学校2021-2022学年高一下学期阶段测试一数
学试题
【答案】(1) (2) (3)
【解析】(1)由题意可知:
(2)
(3)
试卷第22页,共3页
学科网(北京)股份有限公司试卷第23页,共3页
学科网(北京)股份有限公司