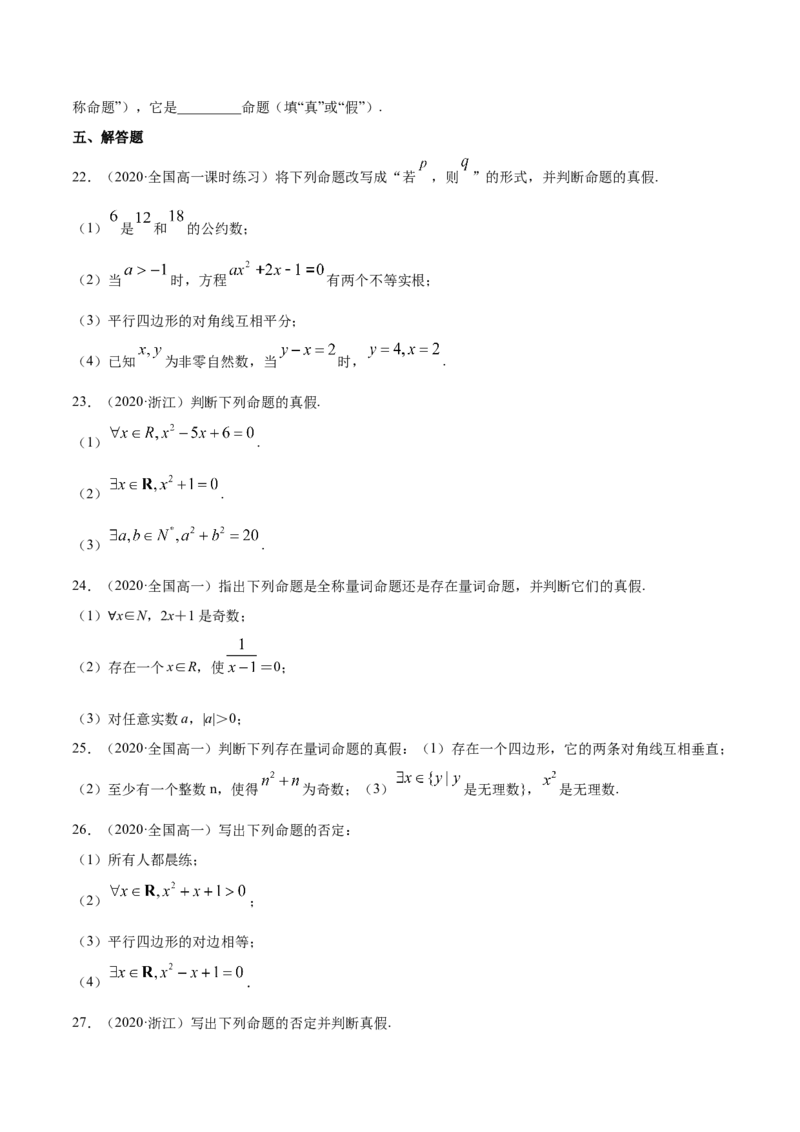文档内容
《常用逻辑用语》单元测试卷
一、单选题
1.(2019·山东济宁·高一月考)命题“ ”的否定是( )
A. B.
C. D.
2.(2020·安徽省六安中学高二期中(文))设p:x<3,q:-14时,方程x2-4x+a=0有实根”是假命题
6.(2020·全国高一课时练习)下列语句:
① ;②作射线AB;③ ;④ 有一个根是-1;⑤ .其中是命题的是( )
A.①②③ B.①③④
C.③ D.②⑤
7.(2020·全国高一课时练习)已知不等式x+3≥0的解集是A,若a∈A是假命题,则a的取值范围是(
)
A.a≥-3 B.a>-3
C.a≤-3 D.a<-3
8.(2020·湖南雨花·雅礼中学高三其他(理))设集合 , ,则“ ”是“ ”
的( )
A.充分不必要条件 B.必要不充分条件.
C.充分必要条件 D.既不充分又不必要条件
9.(2019·内蒙古集宁一中高三月考)命题“存在实数x,,使x > 1”的否定是( )
A.对任意实数x, 都有x > 1 B.不存在实数x,使x 1
C.对任意实数x, 都有x 1 D.存在实数x,使x 1
10.(2019·浙江湖州·高二期中)已知 ,那么“ ”是“ ”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
二、多选题
11.(2020·浙江高一单元测试)下列不等式中可以作为 的一个充分不必要条件的有( )
A. B. C. D.
12.(2020·迁西县第一中学高二期中)下列命题的否定中,是全称命题且是真命题的是( )
A. B.所有正方形都是矩形
C. D.至少有一个实数x,使
13.(2020·山东省桓台第一中学高二期中)(多选)对任意实数 , , ,给出下列命题:
①“ ”是“ ”的充要条件;②“ 是无理数”是“ 是无理数”的充要条件;
③“ ”是“ ”的必要条件;
④“ ”是“ ”的充分条件.
其中真命题是( ).
A.① B.② C.③ D.④
14.(2020·全国高一单元测试)下列命题中,是全称量词命题的有( )
A.至少有一个x使 成立 B.对任意的x都有 成立
C.对任意的x都有 不成立 D.存在x使 成立
E.矩形的对角线垂直平分
三、填空题
15.(2020·全国高一课时练习)把命题“当x=2时,x2-3x+2=0”改写成“若p,则q”的形式:
____________________________.
16.(2020·安徽金安·六安一中高二期中(文))命题“ ”的否定是________.
17.(2020·浙江高一单元测试)已知命题 或 ,命题 或 ,若 是
的充分非必要条件,则实数 的取值范围是________
四、双空题
18.(2020·全国高一课时练习)已知命题:弦的垂直平分线经过圆心并且平分弦所对的弧,若把上述命题
改为“若p,则q”的形式,则p是____________________,q是__________________.
19.(2020·上海)“ ”的一个充分非必要条件可以为________;一个必要非充分条件可以为
________.
20.(2019·宁波中学高二期中)下列语句是命题的有______,其中是假命题的有______.(只填序号)
①等边三角形是等腰三角形吗?
②作三角形的一个内角平分线
③若 为有理数,则 , 也都是有理数.
④ .
21.(2020·广东中山·高二期末)命题 : , 是__________(填“全称命题”或“特称命题”),它是_________命题(填“真”或“假”).
五、解答题
22.(2020·全国高一课时练习)将下列命题改写成“若 ,则 ”的形式,并判断命题的真假.
(1) 是 和 的公约数;
(2)当 时,方程 有两个不等实根;
(3)平行四边形的对角线互相平分;
(4)已知 为非零自然数,当 时, .
23.(2020·浙江)判断下列命题的真假.
(1) .
(2) .
(3) .
24.(2020·全国高一)指出下列命题是全称量词命题还是存在量词命题,并判断它们的真假.
(1) x∈N,2x+1是奇数;
∀
(2)存在一个x∈R,使 =0;
(3)对任意实数a,|a|>0;
25.(2020·全国高一)判断下列存在量词命题的真假:(1)存在一个四边形,它的两条对角线互相垂直;
(2)至少有一个整数n,使得 为奇数;(3) 是无理数}, 是无理数.
26.(2020·全国高一)写出下列命题的否定:
(1)所有人都晨练;
(2) ;
(3)平行四边形的对边相等;
(4) .
27.(2020·浙江)写出下列命题的否定并判断真假.(1)不论m取何实数,方程 必有实数根.
(2)所有末位数是0或5的整数都能被5整除.
(3)某些梯形的对角线互相平分.
(4)被8整除的数能被4整除.