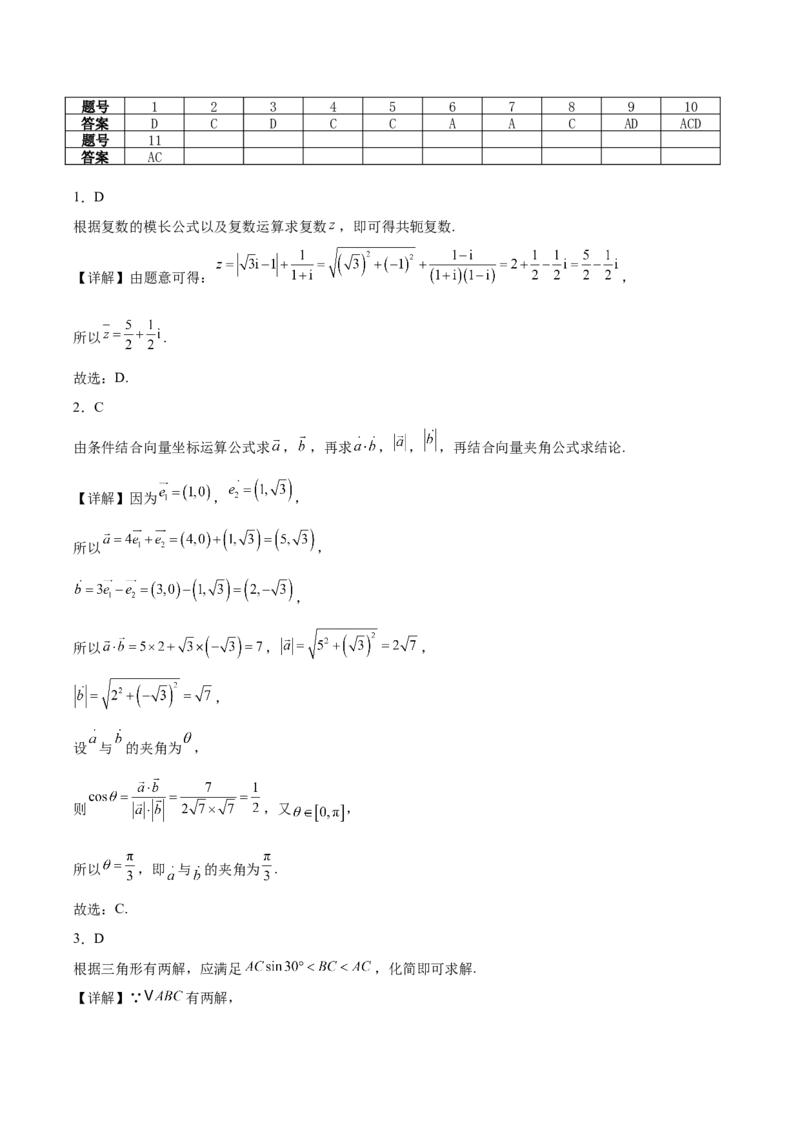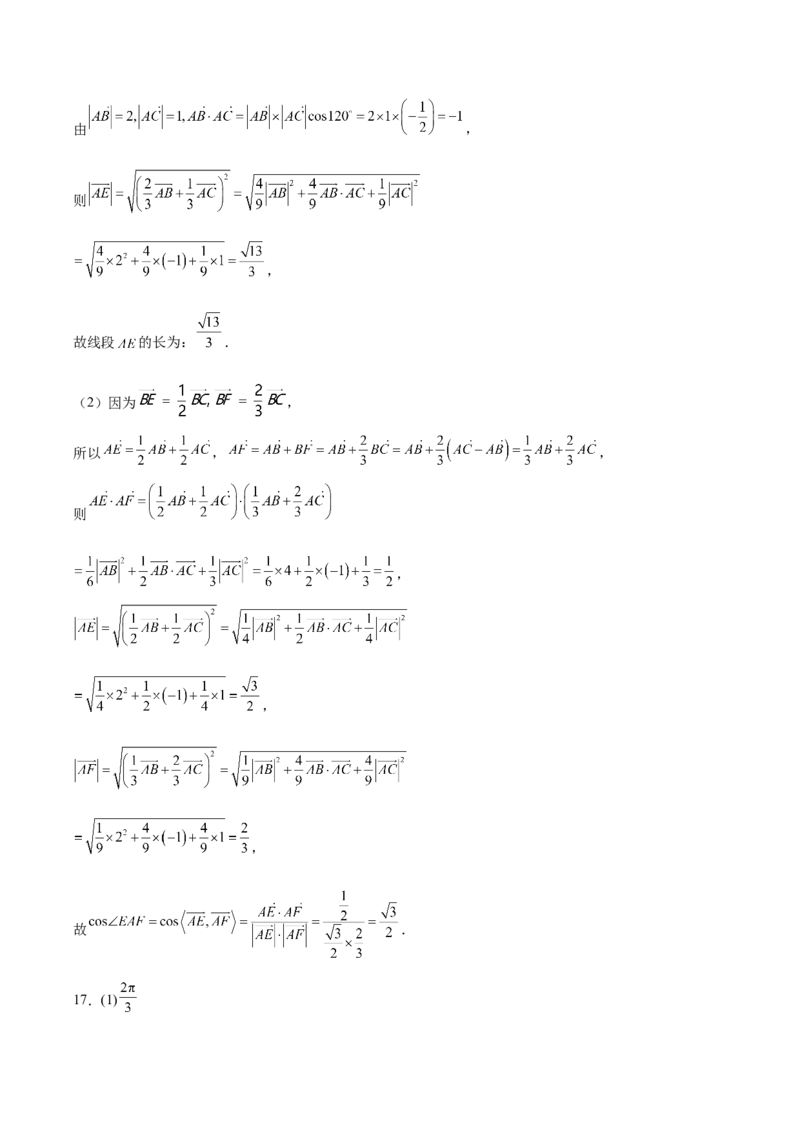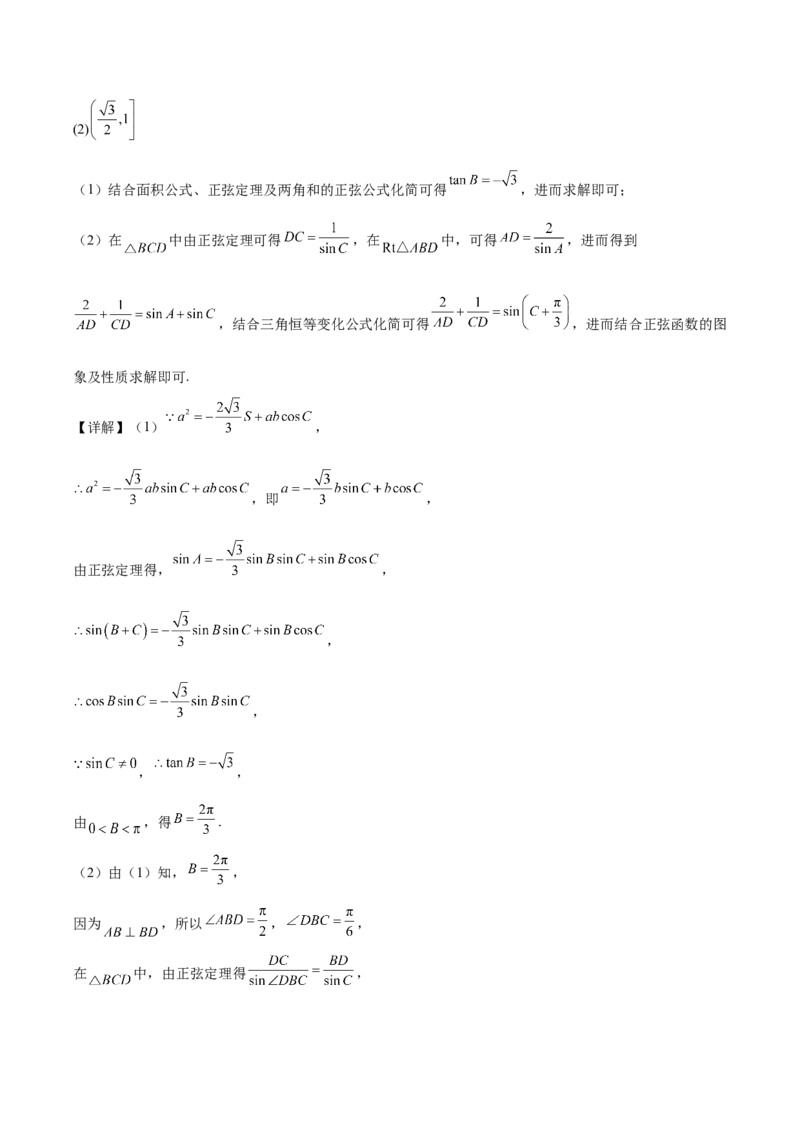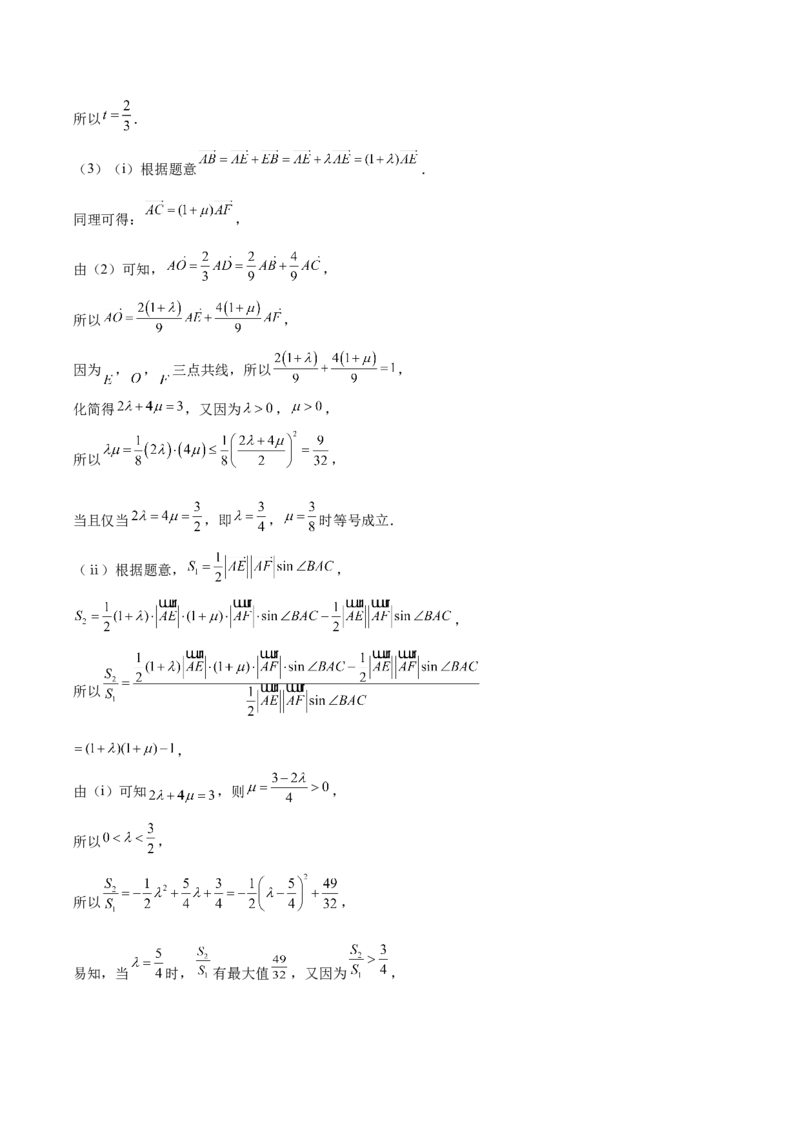文档内容
吉林省长春市十一高中2024-2025学年高一下学期4月月考数学试题
一、单选题
1.已知 ,则复数 的共轭复数 为( ).
A. B. C. D.
2.已知向量 , ,设 , ,则 与 的夹角为( )
A. B. C. D.
3.在 中, , ,满足此条件 有两解,则BC边长度的取值范围为( )
A. B. C. D.
4.在 中,角 所对的边分别为 , 是边 的中点, , 若 ,则边
( ).
A.16 B. C.4 D.8
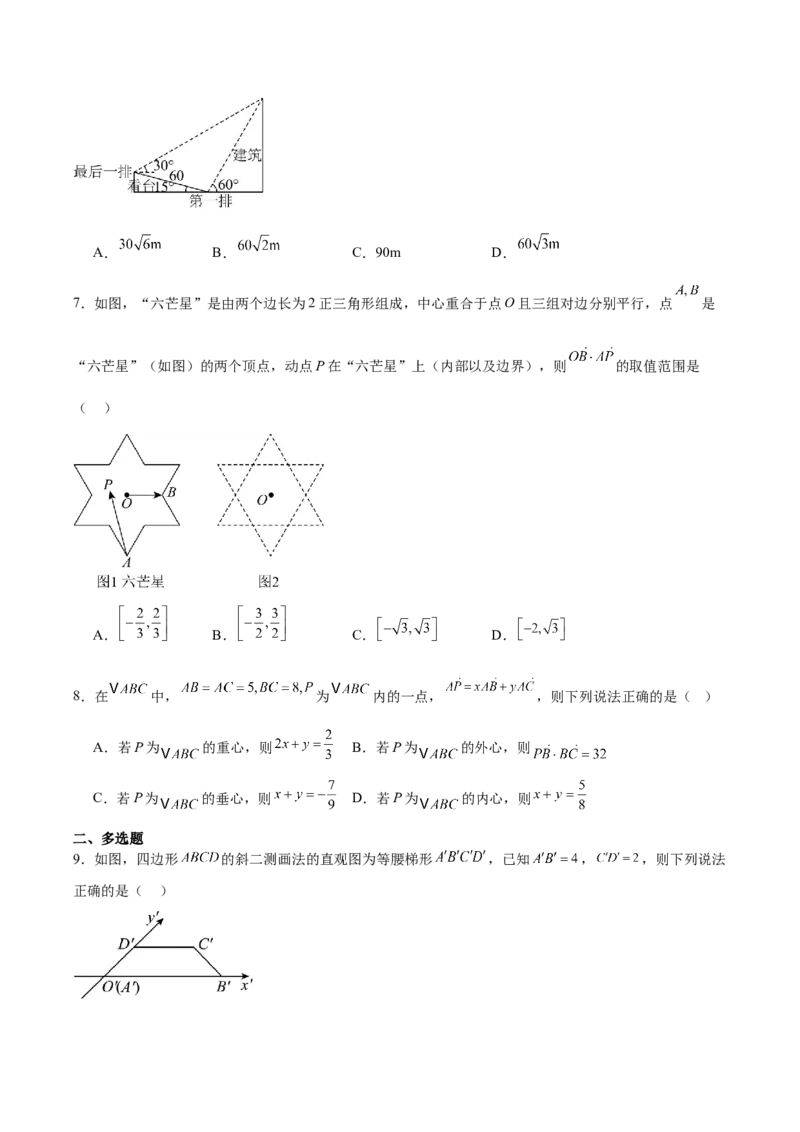
5.如图所示,在正方形 中, 为 的中点, 为 的中点,若 ,则
( )
A. B. C. D.
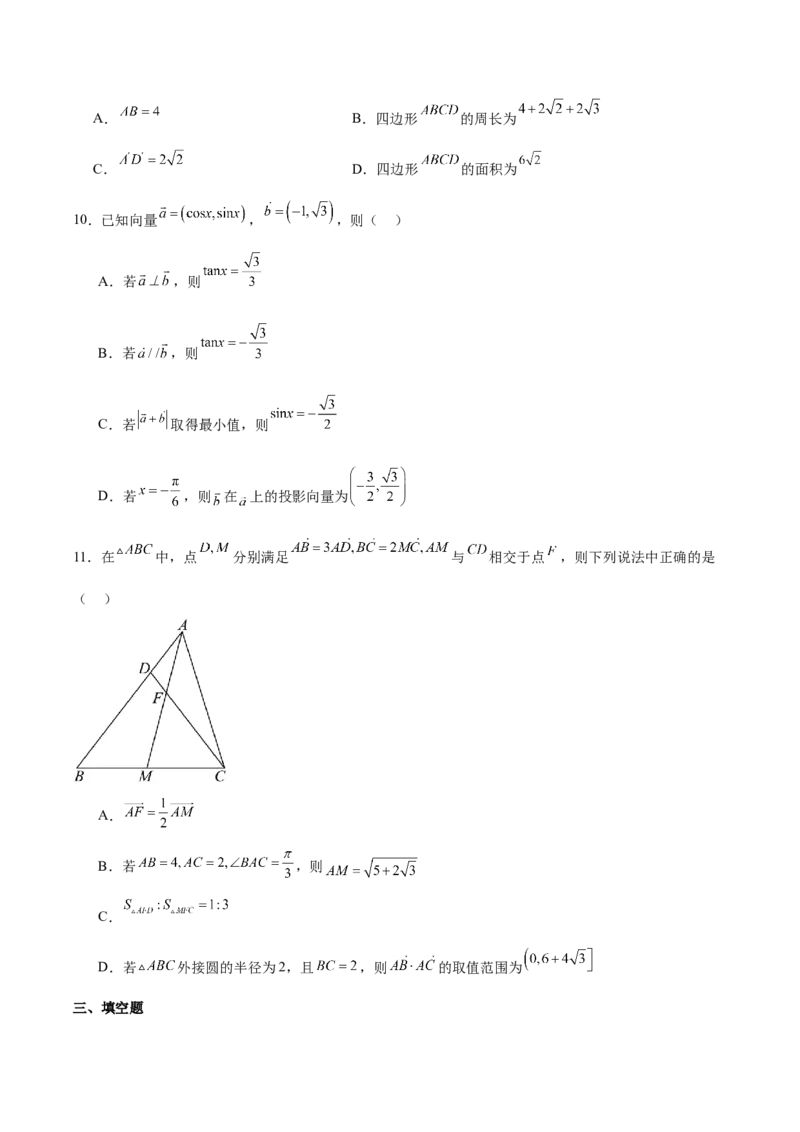
6.结合图示,某坡度为 的看台上,同一列的第一排和最后一排测得地标建筑顶部的仰角为 和 ,
第一排和最后一排的距离为60m,则建筑的高度为( )A. B. C.90m D.
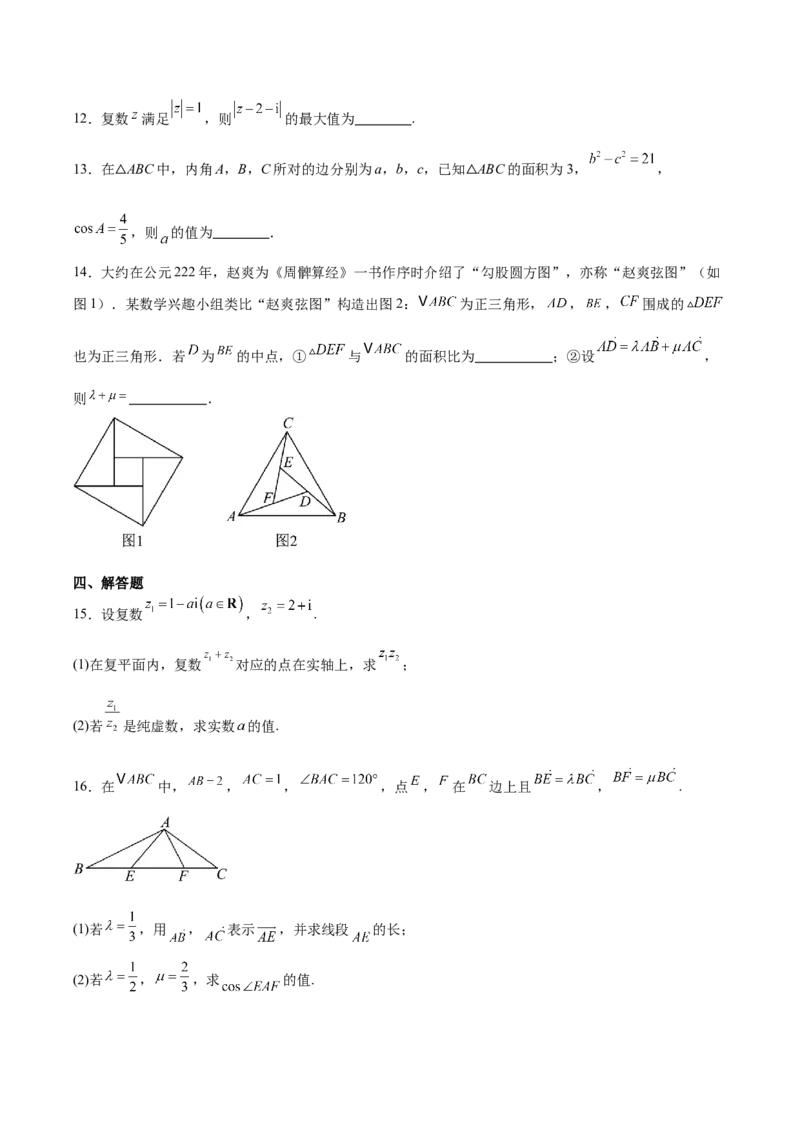
7.如图,“六芒星”是由两个边长为2正三角形组成,中心重合于点O且三组对边分别平行,点 是
“六芒星”(如图)的两个顶点,动点P在“六芒星”上(内部以及边界),则 的取值范围是
( )
A. B. C. D.
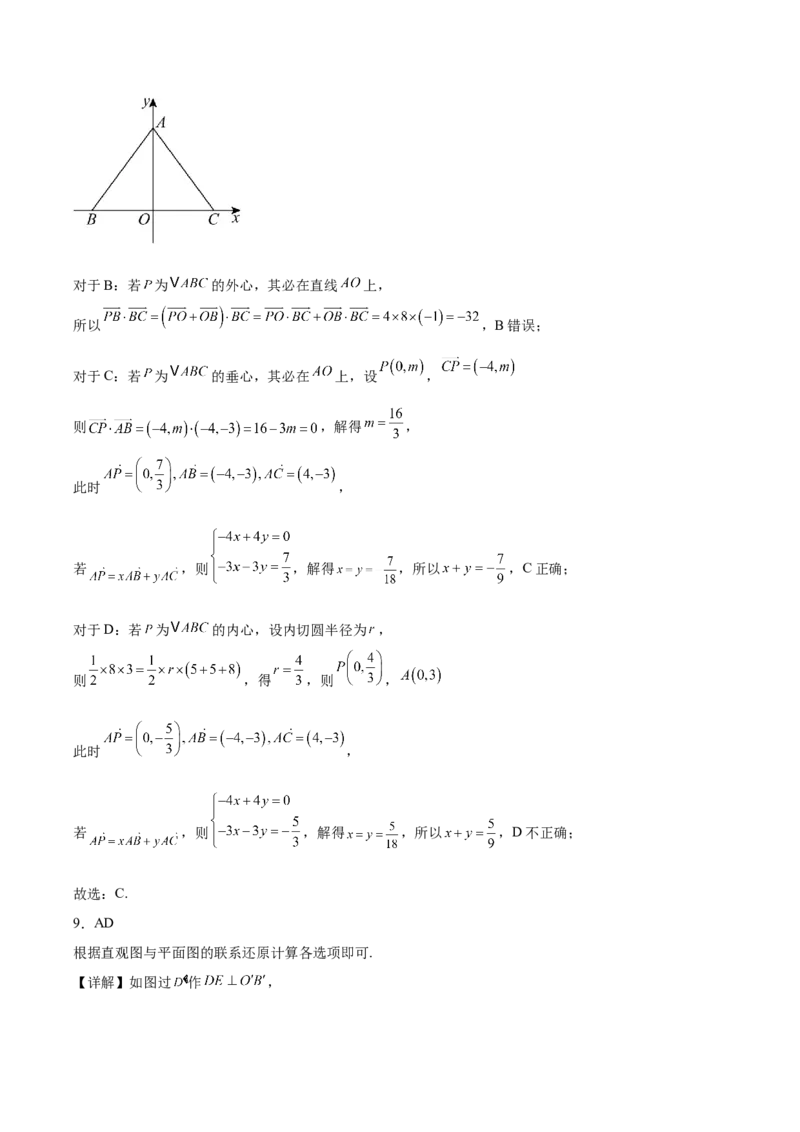
8.在 中, 为 内的一点, ,则下列说法正确的是( )
A.若P为 的重心,则 B.若P为 的外心,则
C.若P为 的垂心,则 D.若P为 的内心,则
二、多选题
9.如图,四边形 的斜二测画法的直观图为等腰梯形 ,已知 , ,则下列说法
正确的是( )A. B.四边形 的周长为
C. D.四边形 的面积为
10.已知向量 , ,则( )
A.若 ,则
B.若 ,则
C.若 取得最小值,则
D.若 ,则 在 上的投影向量为
11.在 中,点 分别满足 与 相交于点 ,则下列说法中正确的是
( )
A.
B.若 ,则
C.
D.若 外接圆的半径为2,且 ,则 的取值范围为
三、填空题12.复数 满足 ,则 的最大值为 .
13.在 ABC中,内角A,B,C所对的边分别为a,b,c,已知 ABC的面积为3, ,
△ △
,则 的值为 .
14.大约在公元222年,赵爽为《周髀算经》一书作序时介绍了“勾股圆方图”,亦称“赵爽弦图”(如
图1).某数学兴趣小组类比“赵爽弦图”构造出图2: 为正三角形, , , 围成的
也为正三角形.若 为 的中点,① 与 的面积比为 ;②设 ,
则 .
四、解答题
15.设复数 , .
(1)在复平面内,复数 对应的点在实轴上,求 ;
(2)若 是纯虚数,求实数 的值.
16.在 中, , , ,点 , 在 边上且 , .
(1)若 ,用 , 表示 ,并求线段 的长;
(2)若 , ,求 的值.17.在 中,内角 所对的边分别是 ,三角形面积为 ,若 为 边上一点,满足
,且 .
(1)求角 ;
(2)求 的取值范围.
18.如图,已知半径为2的扇形 的圆心角为 , 为 的中点, 是 上一动点.
(1)求 的取值范围;
(2)当 为 的中点时,用 表示 ;
(3)若 ,求 的最大值.
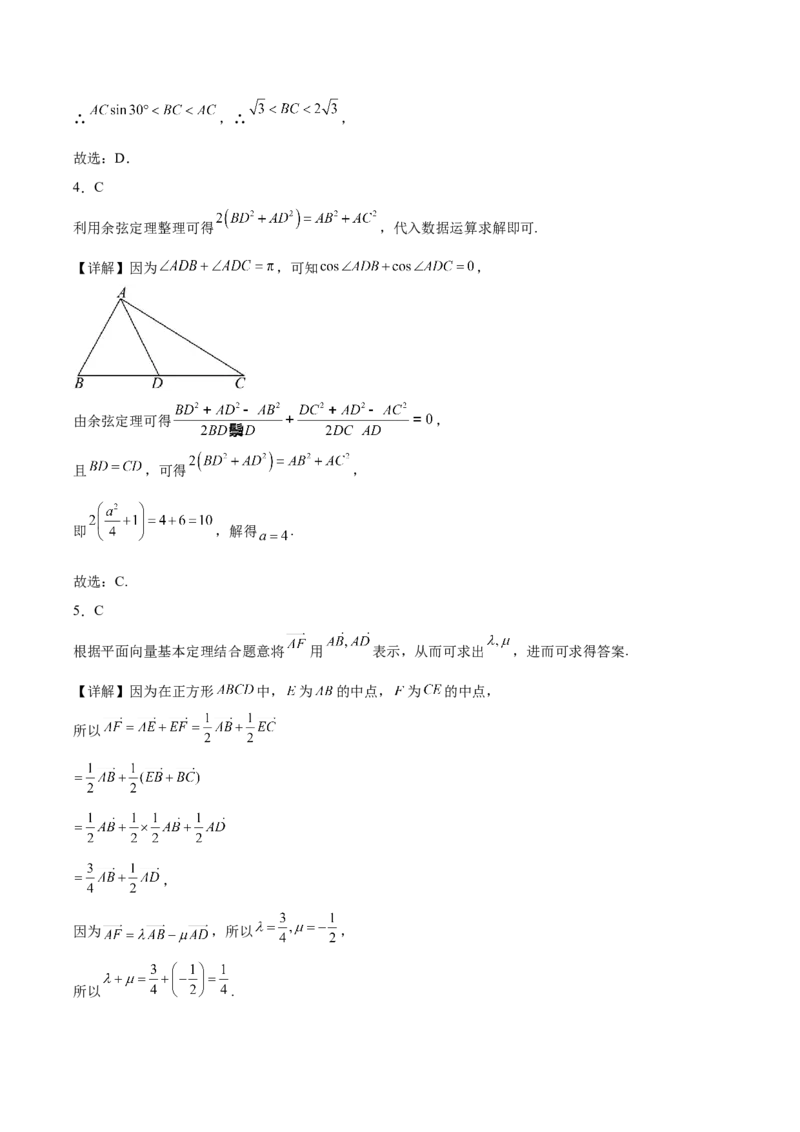
19.如图1所示,在 中,点 在线段 上,满足 , 是线段 上的点,且满足
,线段 与线段 交于点 .
(1)若 ,求实数 的值;
(2)若 ,求实数 的值;(3)如图2,过点 的直线与边 分别交于点 ,设 , ;
(ⅰ)求 的最大值;
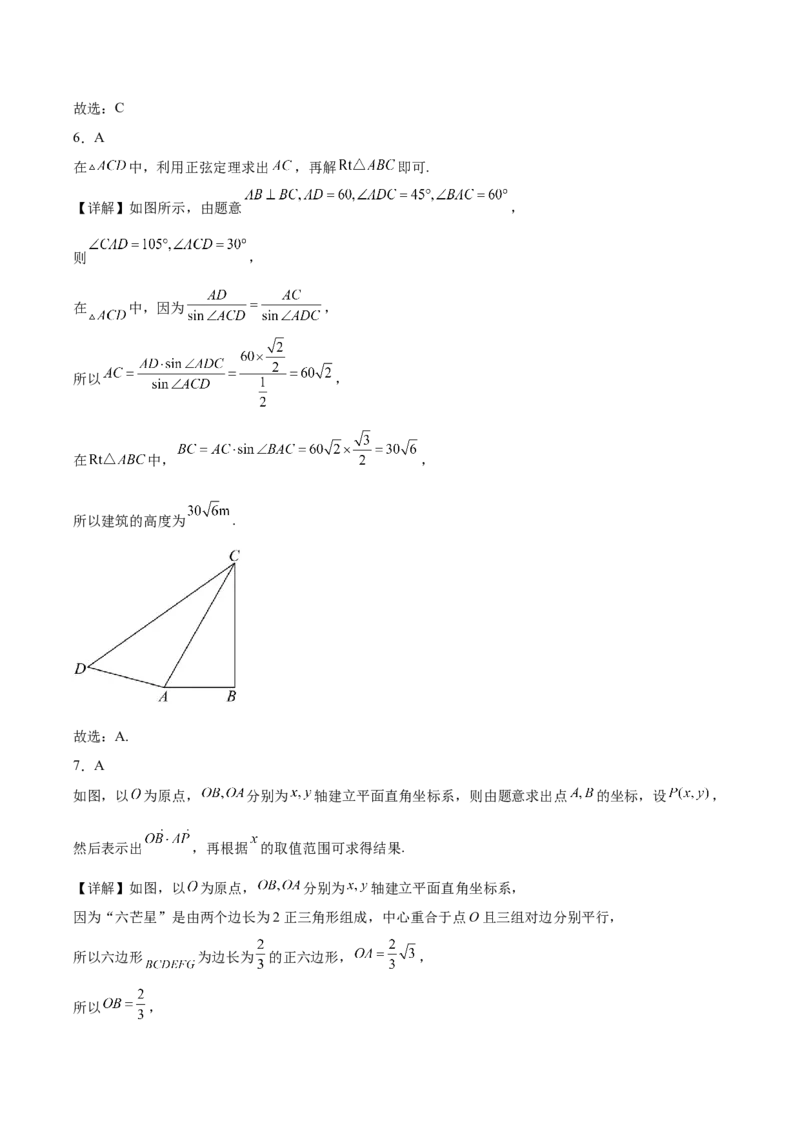
(ⅱ)设 的面积为 ,四边形 的面积为 ,求 的取值范围.题号 1 2 3 4 5 6 7 8 9 10
答案 D C D C C A A C AD ACD
题号 11
答案 AC
1.D
根据复数的模长公式以及复数运算求复数 ,即可得共轭复数.
【详解】由题意可得: ,
所以 .
故选:D.
2.C
由条件结合向量坐标运算公式求 , ,再求 , , ,再结合向量夹角公式求结论.
【详解】因为 , ,
所以 ,
,
所以 , ,
,
设 与 的夹角为 ,
则 ,又 ,
所以 ,即 与 的夹角为 .
故选:C.
3.D
根据三角形有两解,应满足 ,化简即可求解.
【详解】∵ 有两解,∴ ,∴ ,
故选:D.
4.C
利用余弦定理整理可得 ,代入数据运算求解即可.
【详解】因为 ,可知 ,
由余弦定理可得 ,
且 ,可得 ,
即 ,解得 .
故选:C.
5.C
根据平面向量基本定理结合题意将 用 表示,从而可求出 ,进而可求得答案.
【详解】因为在正方形 中, 为 的中点, 为 的中点,
所以
,
因为 ,所以 ,
所以 .故选:C
6.A
在 中,利用正弦定理求出 ,再解 即可.
【详解】如图所示,由题意 ,
则 ,
在 中,因为 ,
所以 ,
在 中, ,
所以建筑的高度为 .
故选:A.
7.A
如图,以 为原点, 分别为 轴建立平面直角坐标系,则由题意求出点 的坐标,设 ,
然后表示出 ,再根据 的取值范围可求得结果.
【详解】如图,以 为原点, 分别为 轴建立平面直角坐标系,
因为“六芒星”是由两个边长为2正三角形组成,中心重合于点O且三组对边分别平行,
所以六边形 为边长为 的正六边形, ,
所以 ,所以 ,
设 ,则 ,
所以 ,
因为动点P在“六芒星”上(内部以及边界),
所以 ,所以 ,
所以 .
故选:A.
8.C
对于ACD:先求出三角形各种心的坐标,然后代入坐标列方程求解;对于B:利用
展开计算即可.
【详解】如图建立平面直角坐标系, ,
对于A:若 为 的重心,则 ,
所以
若 ,则 ,解得 ,所以 ,A不正确;对于B:若 为 的外心,其必在直线 上,
所以 ,B错误;
对于C:若 为 的垂心,其必在 上,设 ,
则 ,解得 ,
此时 ,
若 ,则 ,解得 ,所以 ,C正确;
对于D:若 为 的内心,设内切圆半径为 ,
则 ,得 ,则 ,
此时 ,
若 ,则 ,解得 ,所以 ,D不正确;
故选:C.
9.AD
根据直观图与平面图的联系还原计算各选项即可.
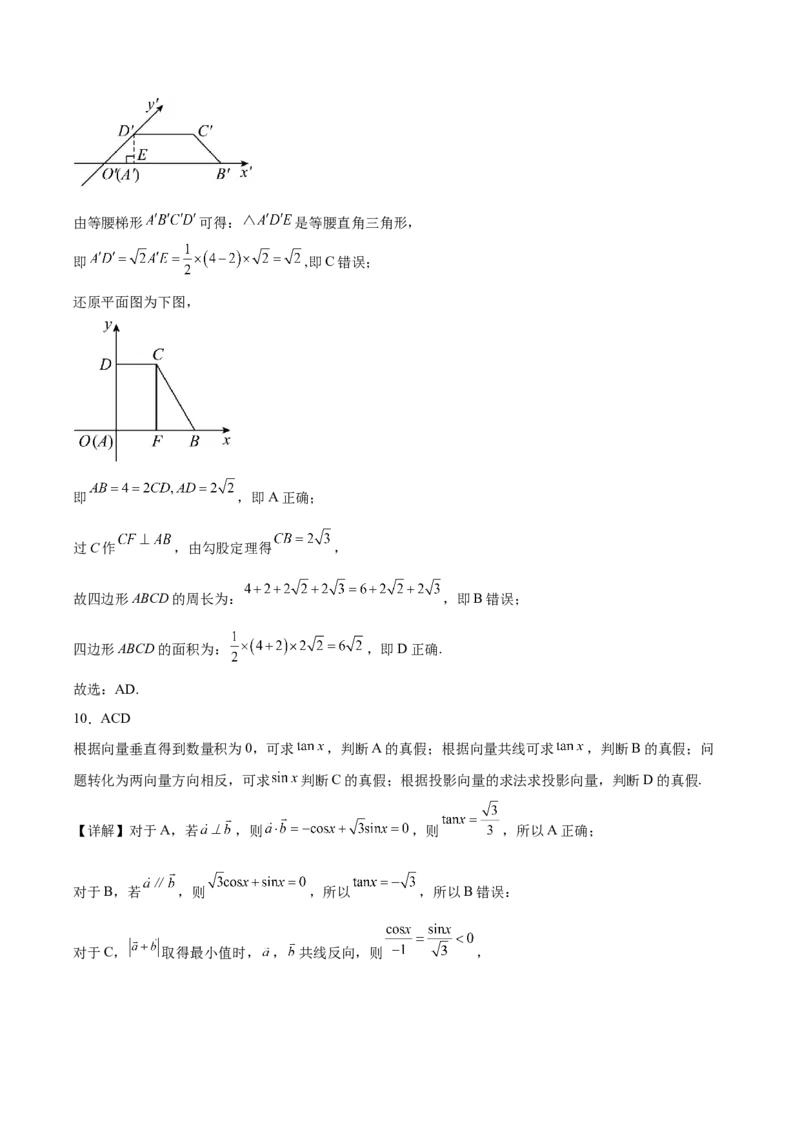
【详解】如图过 作 ,由等腰梯形 可得: 是等腰直角三角形,
即 ,即C错误;
还原平面图为下图,
即 ,即A正确;
过C作 ,由勾股定理得 ,
故四边形ABCD的周长为: ,即B错误;
四边形ABCD的面积为: ,即D正确.
故选:AD.
10.ACD
根据向量垂直得到数量积为0,可求 ,判断A的真假;根据向量共线可求 ,判断B的真假;问
题转化为两向量方向相反,可求 判断C的真假;根据投影向量的求法求投影向量,判断D的真假.
【详解】对于A,若 ,则 ,则 ,所以A正确;
对于B,若 ,则 ,所以 ,所以B错误:
对于C, 取得最小值时, , 共线反向,则 ,解得 ,则 ,所以C正确;
对于D,若 ,则 ,所以 在 上的投影向量为 ,所
以D正确.
故选:ACD
11.AC
对于A,设 ,以向量 为基底表示向量 ,根据 共线求出 即可判断A正确;
对于B,由 得 ,再利用数量积求模即可判断B不正确;对于C,由
知分点 的位置求出 即可判断C正确;对于D,
由题意利用正弦定理求得得 或 ,当 时 ,由此判断D不正确.
【详解】对于A,设 ,因为 则
,
,
由 共线,得 解得 ,所以 ,故A正确;
对于B,由 得 ,
所以所以 ,故B不正确;
对于C,由 知 是 的中点,所以 , ,又 ,所以
,所以 , ,故C正确;
对于D,设 的三边分别为 ,依题意得 ,由外接圆的半径为2,根据正弦定理得 ,
所以 ,由 ,得 或 ,当 时,
,故D不正确.
故选:AC.
12. /
根据题意结合复数的几何意义,可知 表示 所对应的点到点 的距离,从而可可求出
的最大值.
【详解】满足 的复数 所对应的点在以原点为圆心,1为半径的圆上,
的几何意义为 所对应的点到点 的距离,
因为 ,
所以 的最大值为 .
故答案为:13.
先求出 ,再利用面积求出 关系,再结合 求出 ,最后利用余弦定理求出 .
【详解】 ,
,
,
,又 ,
,
.
故答案为: .
14.
①根据类比图形的结构特点,找到 与 的面积联系即可.
②利用向量加减法的三角形法则,用 , 表示出 即可.
【详解】如图:连接 ,由题意知 ,且 分别为 的中点, .
所以 ,
,
得 .
, ,
化简得 ,
所以
故答案为:① ;② .
15.(1)
(2)
(1)先求出 ,再由复数 对应的点在实轴上,求出 的值,从而可求出 ;
(2)先化简 ,再由 为纯虚数可求出实数 的值.
【详解】(1)因为复数 , ,
所以 ,
因为复数 对应的点在实轴上,所以 ,得 ,所以 ,
所以 ;
(2)因为复数 , ,
所以
,
因为 为纯虚数,所以 ,解得 .
16.(1) ,
(2)
(1)由向量的线性运算得到 ,再由向量的模的运算求解;
(2) 因为 ,所以 , ,再分别计算数量积与向量
的模,再由 求解.
【详解】(1)依题意, ,
则 ,
故 ,由 ,
则
,
故线段 的长为: .
(2)因为 ,
所以 , ,
则
,
,
,
故 .
17.(1)(2)
(1)结合面积公式、正弦定理及两角和的正弦公式化简可得 ,进而求解即可;
(2)在 中由正弦定理可得 ,在 中,可得 ,进而得到
,结合三角恒等变化公式化简可得 ,进而结合正弦函数的图
象及性质求解即可.
【详解】(1) ,
,即 ,
由正弦定理得, ,
,
,
, ,
由 ,得 .
(2)由(1)知, ,
因为 ,所以 , ,
在 中,由正弦定理得 ,即 ,
在 中, ,
,
, ,
,
, , ,
所以 的取值范围为 .
18.(1)
(2)
(3)
(1)设 ,则可得 ,结合余弦函数性质求解即可.
(2)由图可得 ,再根据投影向量确定 ,再代入角度求解即可.
(3)结合题意将 用三角函数表示,再利用正弦函数的性质求最大值即可.
【详解】(1)如图,设 ,连接 ,而 ,
因为 ,故 ,
所以 的取值范围为 .
(2)因为 为 的中点,所以 ,
由平面向量加法法则得 ,
则 在 方向上的投影向量为 ,
在 方向上的投影向量为 ,
得到 ,
故 ,
将 代入,得 .
(3)因为 , ,
所以 ,
又由(2)知 ,故 ,则 ,
因为 ,所以当且仅当 时, 取得最大值1,
故 的最大值为 .
19.(1) ,
(2)
(3)(ⅰ) ;(ⅱ)
【详解】(1)因为 ,所以 ,
所以 ,
又 ,且 、 不共线,所以 , ;
(2)因为 、 、 三点共线,所以存在实数 使得 ,
所以 ,
因为 ,即 ,
所以 ,
又因为 ,
即 ,又 、 不共线,
所以 ,解得 ,所以 .
(3)(i)根据题意 .
同理可得: ,
由(2)可知, ,
所以 ,
因为 , , 三点共线,所以 ,
化简得 ,又因为 , ,
所以 ,
当且仅当 ,即 , 时等号成立.
(ⅱ)根据题意, ,
,
所以
,
由(i)可知 ,则 ,
所以 ,
所以 ,
易知,当 时, 有最大值 ,又因为 ,所以 .