文档内容
格致课堂
6.3.2 平面向量的正交分解及坐标表示
一、选择题
1.设i,j是平面直角坐标系内分别与x轴,y轴正方向相同的两个单位向量,O为坐标原点,若OA
=4i+2j,则OA的坐标是( )
A.(4,-2) B.(4,2)
C.(2,4) D.(-4,8)
2.如果用i,j分别表示x轴和y轴正方向上的单位向量,且A(2,3),B(4,2),则AB可以表示为( )
A.2i+3j B.4i+2j
C.2i-j D.-2i+j
3.已知AB=(-2,4),则下列说法正确的是( )
A.A点的坐标是(-2,4)
B.B点的坐标是(-2,4)
C.当B是原点时,A点的坐标是(-2,4)
D.当A是原点时,B点的坐标是(-2,4)
4.若{i,j}为正交基底,设a=(x2+x+1)i-(x2-x+1)j(其中x∈R),则向量a对应的坐标位于(
)
A.第一、二象限 B.第二、三象限
C.第三象限 D.第四象限
5. (多选题)下列说法正确的是( )
A.相等向量的坐标相同;
B.平面上一个向量对应平面上唯一的坐标;
C.一个坐标对应唯一的一个向量;
D.平面上一个点与以原点为始点,该点为终点的向量一一对应。
i⃗ =(1,0),⃗j=(0,1) ⃗a
6.(多选题)已知向量 ,平面内的任意向量 ,下列结论中错误的是( )
⃗a=(x,y)
A.存在唯一的一对实数x,y,使得 。
x ,x ,y ,y ∈R,⃗a=(x ,y )≠(x ,y ), x ≠x ,y ≠y
B.若 1 2 1 2 1 1 2 2 则 1 2 1 2。
x,y∈R,⃗a=(x,y) ⃗a≠0⃗ ⃗a
C.若 ,且 ,则 的起点是原点O。
x,y∈R,⃗a≠0⃗ ⃗a (x,y) ⃗a=(x,y)
D.若 ,且 的终点坐标是 ,则 。
二、填空题
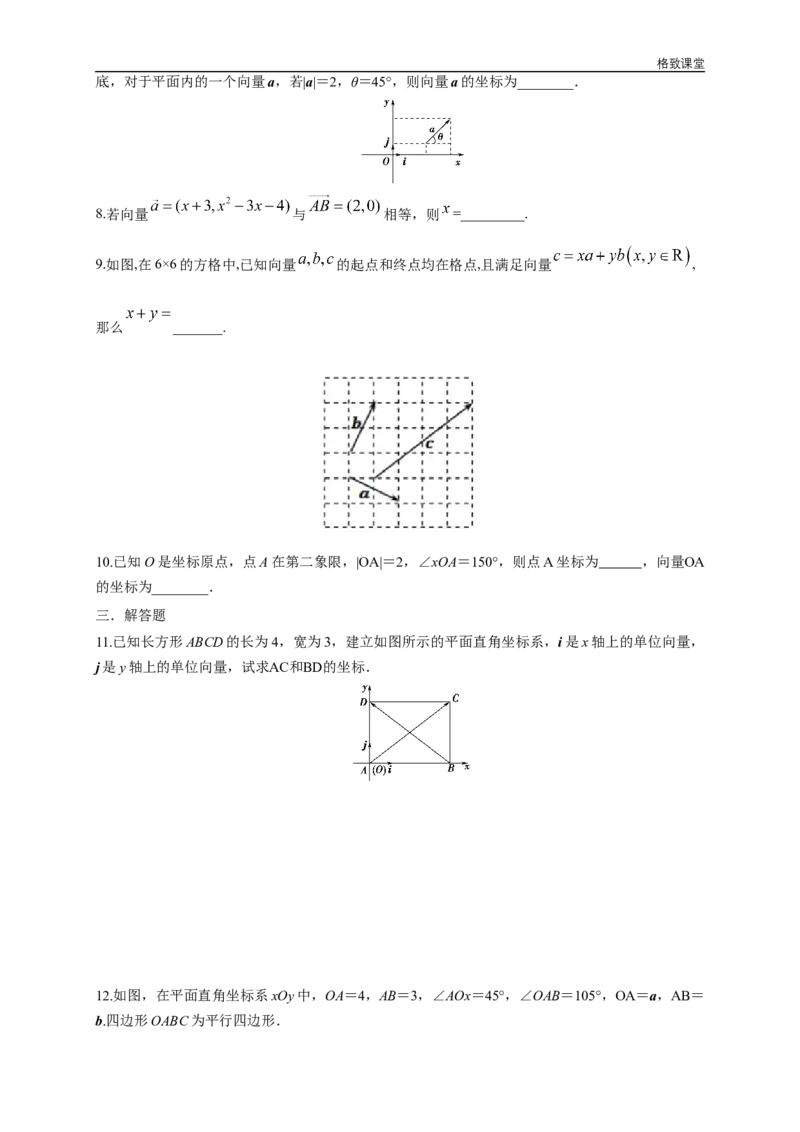
7.如图,在平面直角坐标系中,分别取与x轴,y轴方向相同的两个单位向量i,j,以{i,j}作为基格致课堂
底,对于平面内的一个向量a,若|a|=2,θ=45°,则向量a的坐标为________.
8.若向量 与 相等,则 =_________.
9.如图,在6×6的方格中,已知向量 的起点和终点均在格点,且满足向量 ,
那么 _______.
10.已知O是坐标原点,点A在第二象限,|OA|=2,∠xOA=150°,则点A坐标为 ,向量OA
的坐标为________.
三.解答题
11.已知长方形ABCD的长为4,宽为3,建立如图所示的平面直角坐标系,i是x轴上的单位向量,
j是y轴上的单位向量,试求AC和BD的坐标.
12.如图,在平面直角坐标系xOy中,OA=4,AB=3,∠AOx=45°,∠OAB=105°,OA=a,AB=
b.四边形OABC为平行四边形.格致课堂
(1)求向量a,b的坐标;
(2)求向量BA的坐标;
(3)求点B的坐标.