文档内容
格致课堂
人教A版 第二册 第十章 概率 小结与回顾
一、选择题
1.在一次随机试验中,三个事件 , , 的概率分别为0.2,0.3,0.5,则下列说法正确的个数是(
)
① 与 是互斥事件,也是对立事件;
② 是必然事件;
③ ;
④ .
A.4 B.1 C.2 D.3
【答案】B
【解析】三个事件 , , 不一定是互斥事件,故 , ,
; 与 不一定是互斥事件,也不一定是对立事件.④正确.
2.经统计,某储蓄所一个营业窗口等候的人数及相应的概率如表:
排队人数 0 1 2 3 4 5人及以上
概率 .1 0.16 0.3 0.3 0.1 0.04
则至少3人排队等候的概率是( )
A.0.44 B.0.56 C.0.86 D.0.14
【答案】A
【解析】设至少3人排队等候为事件 ,则有 故选:
3.《史记》中讲述了田忌与齐王赛马的故事:“田忌的上等马优于齐王的中等马,劣于齐王的上等马;
田忌的中等马优于齐王的下等马,劣于齐王的中等马;田忌的下等马劣于齐王的下等马.”若双方各自拥有
上、中、下等马各1匹,从中随机选1匹进行1场比赛,则齐王的马获胜的概率为( )格致课堂
A. B. C. D.
【答案】A
【解析】依题意,记田忌的上等马、中等马、下等马分别为 , , ,齐王的上等马、中等马、下等马
分别为 , , .由题意可知,可能的比赛为 , , , , , , , , ,共9
种,其中田忌可以获胜的事件为 , , ,共3种,则齐王的马获胜的概率 .
4.某城市有连接8个小区 、 、 、 、 、 、 、 和市中心 的整齐方格形道路网,每个小方
格均为正方形,如图所示,某人从道路网中随机地选择一条最短路径,由小区 前往小区 ,则他经过市
中心 的概率是( )
A. B. C. D.
【答案】B
【解析】此人从小区A前往H的所有最短路径为:A→G→O→H,A→E→O→H,A→E→D→H,共3条.
记“此人经过市中心O”为事件M,则M包含的基本事件为:A→G→O→H,A→E→O→H,共2条.
∴ ,即他经过市中心的概率为 ,故选B.
5.(多选题)下列有关古典概型的四种说法:
A.试验中所有可能出现的样本点只有有限个;
B.每个事件出现的可能性相等;
C.每个样本点出现的可能性相等;格致课堂
D.已知样本点总数为 ,若随机事件 包含 个样本点,则事件 发生的概率 .
其中正确的是
【答案】ACD
【解析】B中所说的事件不一定是样本点,所以B不正确;根据古典概型的特点及计算公式可知ACD正
确.
6.(多选题)下列各对事件中,为相互独立事件的是( )
A.掷一枚骰子一次,事件M“出现偶数点”;事件N“出现3点或6点”
B.袋中有3白、2黑共5个大小相同的小球,依次有放回地摸两球,事件M“第一次摸到白球”,事件N“第二次
摸到白球”
C.袋中有3白、2黑共5个大小相同的小球,依次不放同地摸两球,事件M“第一次摸到白球”,事件N“第二次
摸到黑球”
D.甲组3名男生,2名女生;乙组2名男生,3名女生,现从甲、乙两组中各选1名同学参加演讲比赛,事件M“从
甲组中选出1名男生”,事件N“从乙组中选出1名女生”
【答案】ABD
【解析】在A中,样本空间 ,事件 ,事件 ,事件 ,
∴ , , ,即 ,故事件M与N相互
独立,A正确.在B中,根据事件的特点易知,事件M是否发生对事件发生的概率没有影响,故M与N是
相互独立事件,B正确;在C中,由于第1次摸到球不放回,因此会对第2次摸到球的概率产生影响,因
此不是相互独立事件,C错误;在D中,从甲组中选出1名男生与从乙组中选出1名女生这两个事件的发
生没有影响,所以它们是相互独立事件,D正确.故选:ABD.
二、填空题
7.下列说法:
①频率是反映事件发生的频繁程度,概率是反映事件发生的可能性大小;
②百分率是频率,但不是概率;
③频率是不能脱离试验次数 的实验值,而概率是具有确定性的不依赖于试验次数的理论值;
④频率是概率的近似值,概率是频率的稳定值.
其中正确的是______________.格致课堂
【答案】①③④
【解析】对于①,由频率和概率概念: 频率是反映事件发生的频繁程度,概率是反映事件发生的可能性大小.
可知①正确;对于②,概率也可以用百分率表示,故②错误.对于③,频率与试验次数相关,而概率与试验次数无
关,所以③正确;对于④,对于不同批次的试验,频率不一定相同,但概率相同,因而频率是概率的近似值,概率是
频率的稳定值,所以④正确.由概率和频率的定义中可知①③④正确.
8.袋子中有四个小球,分别写有“和、平、世、界”四个字,有放回地从中任取一个小球,直到”
和””平”两个字都取到就停止,用随机模拟的方法估计恰好在第三次停止的概率.利用电脑随机产生0
到3之间取整数值的随机数,分别用0,1,2,3代表“和、平、世、界”这四个字,以每三个随机数为一
组,表示取球三次的结果,经随机模拟产生了以下24个随机数组:
232 321 230 023 123 021 132 220 011 203 331 100
231 130 133 231 031 320 122 103 233 221 020 132
由此可以估计,恰好第三次就停止的概率为_____.
【答案】
【解析】由题意知满足条件的随机数组中,
前两次抽取的数中,含0与1不能同时出现,出现0就不能出现1,出现1就不能出现0,
第三次必须出现前两个数字中没有出现的1或0,
即符合条件的数组只有3组,分别为:021,130,031,
∴恰好第三次就停止的概率为p .
9.一个三位自然数百位,十位,个位上的数字依次为a,b,c,当且仅当有两个数字的和等于第三个
数字时称为“有缘数”(如213,134等),若 ,且a,b,c互不相同,则这个三位
数为”有缘数”的概率是__________.
【答案】
【解析】由1,2,3组成的三位自然数为123,132,213,231,312,321,共6个;
同理由1,2,4组成的三位自然数共6个;
由1,3,4组成的三位自然数也是6个;格致课堂
由2,3,4组成的三位自然数也是6个.
所以共有6+6+6+6=24个.
由1,2,3组成的三位自然数,共6个”有缘数”.
由1,3,4组成的三位自然数,共6个”有缘数”.
所以三位数为”有缘数”的概率 .
10.某学校进行足球选拔赛,有甲、乙、丙、丁四个球队,每两队要进行一场比赛,开始记分规则为:胜
一场得3分,平一场得1分,负一场得0分,甲胜乙、丙、丁的概率分别是0.5、0.6、0.8,甲负乙、丙、
丁的概率分别是0.3、0.2、0.1,最后得分大于等于7胜出,则甲胜出的概率为________.
【答案】0.446
【解析】两人比赛,一人胜、平、负是互斥事件,因此由题意甲平乙、丙、丁的概率分别是0.2、0.2、
0.1,所以甲胜的概率为 .
三、解答题
11.2019年,我国施行个人所得税专项附加扣除办法,涉及子女教育、继续教育、大病医疗、住房贷款利
息或者住房租金、赡养老人等六项专项附加扣除.某单位老、中、青员工分别有72,108,120人,现采用
分层抽样的方法,从该单位上述员工中抽取25人调查专项附加扣除的享受情况.
项目
A B C D E F
员工
子女教育 ○ ○ × ○ × ○
继续教育 × × ○ × ○ ○
大病医疗 × × × ○ × ×
住房贷款利
○ ○ × × ○ ○
息
住房租金 × × ○ × × ×
赡养老人 ○ ○ × × × ○
(1)应从老、中、青员工中分别抽取多少人?
(2)抽取的25人中,享受至少两项专项附加扣除的员工有6人,分别记为A,B,C,D,E,F.享受情况
如下表,其中“○”表示享受,“×”表示不享受.现从这6人中随机抽取2人接受采访.格致课堂
①试用所给字母列举出所有可能的抽取结果;
②设M为事件“抽取的2人享受的专项附加扣除至少有一项相同”,求事件M发生的概率.
【答案】(1)从老、中、青员工中分别抽取6人,9人,10人
(2)① , , , , , , , , , ,
,共11种 ②
【解析】(1)由已知,老、中、青员工人数之比为 ,由于采用分层抽样的方法从中抽取25位员工,
因此应从老、中、青员工中分别抽取6人,9人,10人.
(2)①从已知的6人中随机抽取2人的所有可能结果为 , , , , ,
, , , , , , , , , ,共15种.
②由题中表格知,符合题意的所有可能结果为 , , , , , ,
, , , , ,共11种.
所以,事件M发生的概率 .
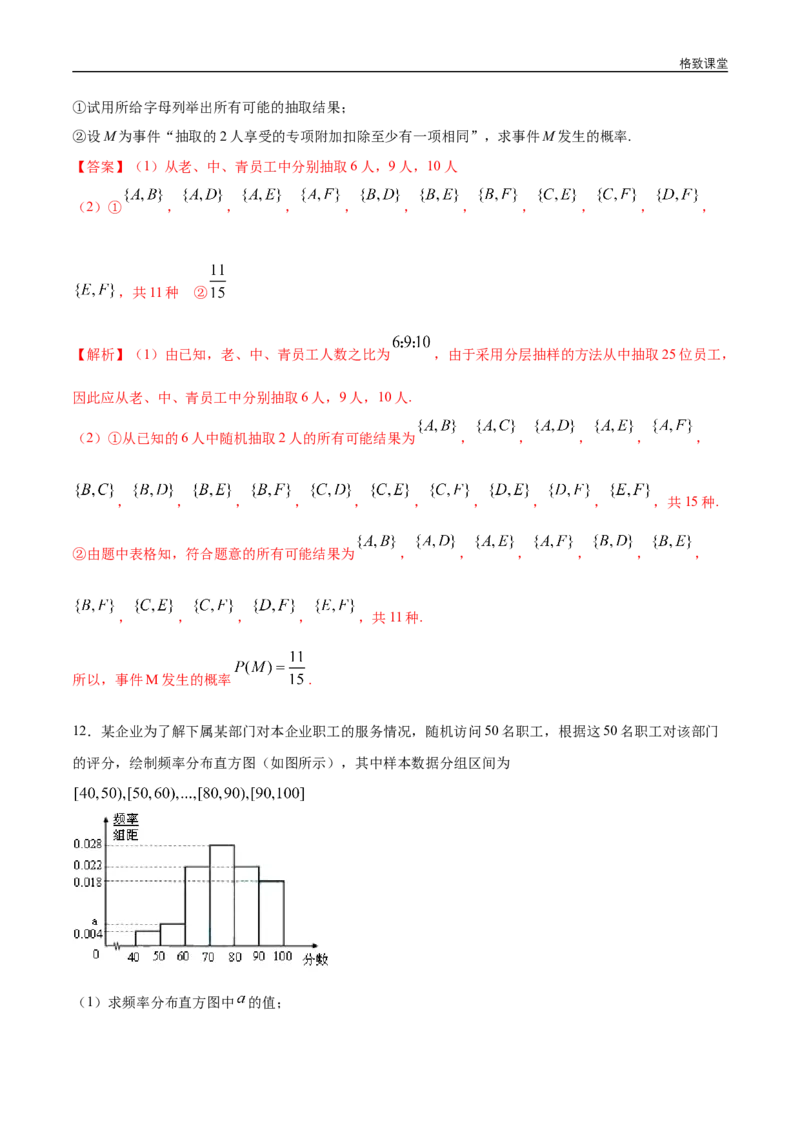
12.某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门
的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为
(1)求频率分布直方图中 的值;格致课堂
(2)估计该企业的职工对该部门评分不低于80的概率;
(3)从评分在 的受访职工中,随机抽取2人,求此2人评分都在 的概率.
【答案】(Ⅰ)0.006;(Ⅱ) ;(Ⅲ)
【解析】(Ⅰ)因为 ,所以 ……..4分)
(Ⅱ)由所给频率分布直方图知,50名受访职工评分不低于80的频率为 ,
所以该企业职工对该部门评分不低于80的概率的估计值为 ………8分
(Ⅲ)受访职工评分在[50,60)的有:50×0.006×10=3(人),即为 ;
受访职工评分在[40,50)的有: 50×0.004×40=2(人),即为 .
从这5名受访职工中随机抽取2人,所有可能的结果共有10种,它们是
又因为所抽取2人的评分都在[40,50)的结果有1种,
即 ,故所求的概率为