文档内容
高一数学教学质量检测
2026.1
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只
有一项是符合题目要求的。
1.“α是第一象限角”是“α是锐角”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既非充分也非必要条件
1
2.函数f (x)=ln(x+2)+ 的定义域是( )
x
A. (−2,+∞) B. [−2,+∞) C. (−∞,−2) D. (−2,0)∪(0,+∞)
3.函数f(x)=2x+x−4的零点所在的区间为( )
A. (0,1) B. (1,2) C. (2,3) D. (3,4)
4.已知a=log 3,b=1.20.3,c=0.31.2,则( )
0.5
A. a0
,则( )
f (x)= 2
−2x2−4x−1,x≤0
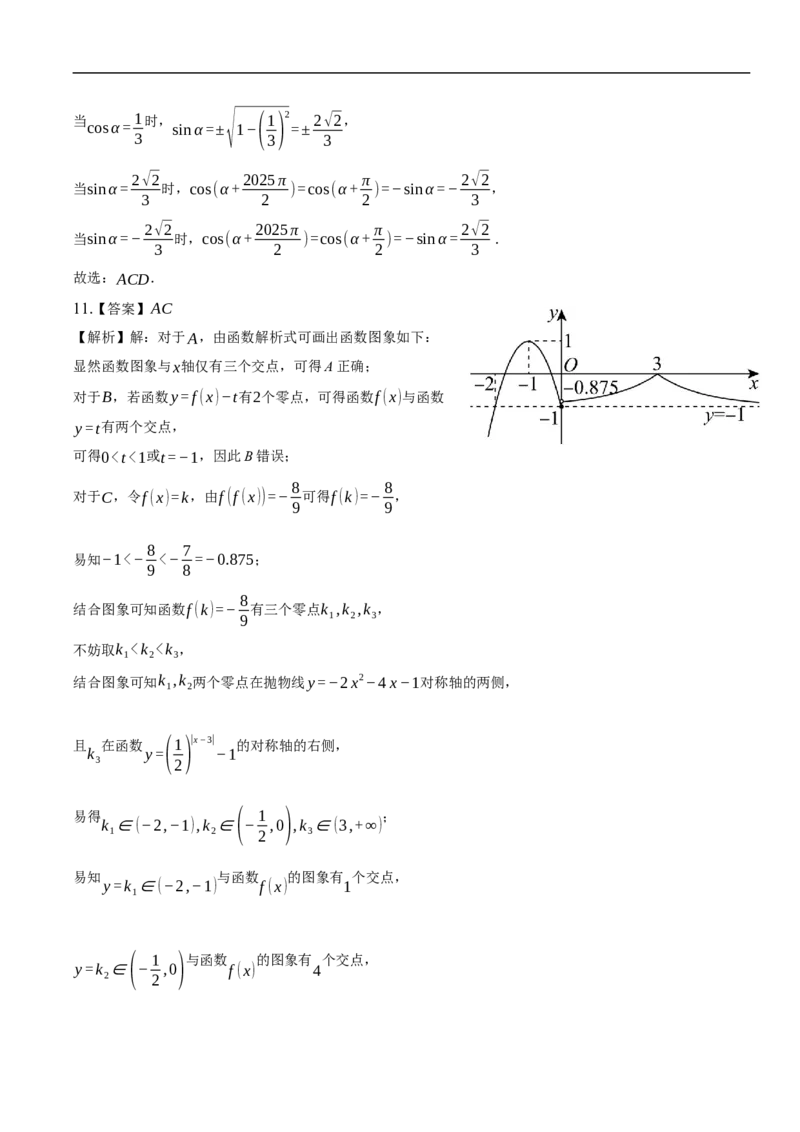
A. 函数f (x)有3个零点
B. 若函数y=f (x)−t有2个零点,则01,且 − =2,则a= .
log 2 log a
a 8
14.已知函数f(x)=ex+e−x,若bf(x)⩽f(2x)+11恒成立,则b的最大值
为 .
四、解答题:本题共5小题,共74分。解答应写出文字说明,证明过程或演算步
骤。
15.(本小题13分)
sin(π−x)cos(2π−x)
已知f (x)= .
( π)
sin x− cos(π+x)
2
求 (5π) 的值;
(1) f
3
若 ,求 的值.
(2) f (x)=2 2sin2x−3sinxcosx
16.(本小题15分)x
已知函数y=f(x),满足f(x−1)=ln .
2−x
求 的解析式;
(1) f(x)
判断函数 的奇偶性;
(2) y=f(x)
解不等式 .
(3) f(x)⩽0
17.(本小题15分)
已知函数 ( π)
f(x)=sin 2x+ ,x∈R
6
求函数 的最小正周期;
(1) f(x)
求函数 的单调递增区间;
(2) f(x)
π
(3) 若x∈[0, ],求函数f(x) 的最值及其相应的x值.
2
18.(本小题17分)
已知函数f(x)=4x−2x−6.
若 ,求 的取值范围;
(1) f(x)<0 x
若关于 的方程 有两个不相等的实数根,设为 , .
(2) x f(x)=m x x
1 2
求 的取值范围;
(i) m
证明: .
(ii) x +x <−2
1 219.(本小题17分)
设函数 且 , ,已知 , .
f(x)=log (ax−b)(a>0 a≠1 b∈R) f(2)=1 f(log 6)=2
a a
求 的定义域;
(1) f(x)
是否存在实数 ,使得 在区间 上的值域是 ?若存在,请求
(2) λ f(x) [m,n] [2m−λ,2n−λ]
出λ的取值范围;若不存在,请说明理由.答案和解析
9π
1.【答案】B 【解析】解:α是锐角,则α是第一象限角,但α是第一象限角,不一定是锐角,如α= ,
4
故“α是第一象限角”是“α是锐角”的必要不充分条件.
{x+2>0
2.【答案】D 【解析】解:由已知可得 ,所以x>−2且x≠0,
x≠0
1
所以函数f (x)=ln(x+2)+ 的定义域是(−2,0)∪(0,+∞).
x
3.【答案】B 【解析】解:易得函数f(x)在R上单调递增,且函数图象连续,
由题知 , , , ,
f(0)=20+0−4=−3<0 f(1)=21+1−4=−1<0 f(2)=22+2−4=2>0 f(3)=23+3−4=7>0
,
f(4)=24+4−4=16>0
因为f(1)⋅f(2)<0,所以(1,2)是函数f(x)的零点所在的一个区间.
4.【答案】B 【解析】解:y=log x在(0,+∞)上单调递减,则log 31.20=1;又y=0.3x单调递减,所以0<0.31.2<0.30=1,
所以an,可得D错误.
π π
【答案】[−1,1] 或{y|−1≤ y≤1}解:因为x∈[− , ],所以tanx∈[−1,1],所以函数f(x)的值域为
4 4
12.
[−1,1]
1 1 3
13.【答案】8 解:因为 − =2,所以log a− =2,
log 2 log a 2 log a
a 8 2
3
令t=log a>0,则t− =2,化简得t2−3=2t,即t2−2t−3=0,解得t=3或t=−1(舍去),
2 t
故log a=3,解得a=8,符合题意.故答案为:8
2
14.【答案】 ,当且仅当 ,即 时取等号,
6 f(x)=ex+e−x ⩾2√ex ⋅e−x=2 ex=e−x x=0
所以 ,
f(2x)=e2x+e−2x=(ex+e−x
)
2−2=[f(x)] 2−2
不等式 可化为 ,
bf(x)⩽f(2x)+11 bf(x)⩽[f(x)] 2+9
所以 9 恒成立,而 9 √ 9 ,
b⩽f(x)+ f(x)+ ⩾2 f(x)⋅ =6
f(x) f(x) f(x)
9
当且仅当f(x)= ,即f(x)=3时取等号,因此b⩽6,所以b的最大值为:6.
f(x)
sin(π−x)cos(2π−x) sinxcosx
15.【答案】解: 因为f (x)= = =tanx,......3分
(1) ( π) −cosx⋅(−cosx)
sin x− cos(π+x)
2所以 (5π) 5π ( π) π .......6分
f =tan =tan 2π− =−tan =−√3
3 3 3 3
因为 ,所以
2sin2x−3sinxcosx
(2) f (x)=tanx=2 2sin2x−3sinxcosx=
sin2x+cos2x
2tan2x−3tanx 2×22−3×2 2.......13分
= = =
tan2x+1 22+1 5
x
16.【答案】解:(1)因为f(x−1)=ln ,
2−x
x
所以 >0,所以01或x≤0,.....14分
1−x
又因为−10
则 可化为 ,
f(x)=4x−2x−6 g(t)=t2−t−6
若f(x)<0,则g(t)<0,即t2−t−6<0,
解得 ,得到 ,解得 ,......2分
t∈(0,3) 2x∈(0,3) x∈(−∞,log 3)
2
则x的取值范围为(−∞,log 3).......4分
2
(2)(i)若关于x的方程f(x)=m有两个不相等的实数根,
则方程g(t)=m有两个不相等的正实数根,
得到g(t)与y=m有两个不相同的横坐标大于0的交点,......6分
1 1
由二次函数性质得g(t)在(0, )上单调递减,在( ,+∞)上单调递增,......8分
2 2
1 25 25
而g(0)=−6,g(t)最小值为g( )=− ,故m∈(− ,−6),......10分
2 4 4
(ii)因为方程g(t)=m有两个不相等的正实数根,
所以t2−t−6−m=0有两个不相等的正实数根,......12分
而我们把方程f(x)=m的两个根设为x ,x ,
1 2
则设 的两个根为 ,
t2−t−6−m=0 t =2x 1,t =2x 2
1 2
由韦达定理得t t =−6−m,即2x 1×2x 2=2x 1 +x 2=−6−m,......14分
1 2
25 1
结合m∈(− ,−6),得到−6−m∈(0, ),......16分
4 4
19.【答案】解: 由 ,得 ,即 ,
(1) f(2)=1 log (a2−b)=1 a2−a−b=0
a
由f(log 6)=2,得log (6−b)=2,即6−b=a2,......2分
a a
3
∴2a2−a−6=0,解得a=2,或a=− (舍),b=2,......4分
2. , ,......5分
∴f(x)=log (2x−2) ∵2x−2>0 ∴x>1
2
故f(x)的定义域为(1,+∞).......6分
(2)假设存在实数λ,n>m>1,使得f(x)在区间[m,n]上的值域是[2m−λ,2n−λ].
由(1)易知f(x)在(1,+∞)上单调递增,......8分
{log (2m−2)=2m−λ
∴ 2 ......10分
log (2n−2)=2n−λ,
2
即{22m−λ=2m−2.......12分
22n−λ=2n−2
令 , , ,
t =2m t =2n t =2λ (t >t >2)
1 2 0 2 1
即 , 为方程 的两个不等实数根且 ,
t t t2−t t+2t =0 t >t >2
1 2 0 0 2 1
令 ,......13分
g(t)=t2−t t+2t
0 0
Δ=t2−8t >0
0 0
则 t 解得 .即 ,......15分
{ 0>2 , t >8 2λ>8
0
2
g(2)>0
即λ>3,故存在实数λ符合条件,λ的取值范围是(3,+∞). ......17分