文档内容
2024~2025 学年下学期佛山市普通高中教学质量检测
高一数学
2025.6
本试卷共4页、19小题.满分150分.考试用时120分钟.
注意事项:
1.答卷前,考生务必要填涂答题卷上的有关项目.
2.选择题每小题选出答案后,用2B铅笔把答案涂在答题卷相应的位置上.
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卷各题目指定区域内:
如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液,不按以上要
求作答的答案无效.
4.请考生保持答题卷的整洁.考试结束后,将答题卷交回.
一、选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项
是符合题目要求的.
1. ( )
A. B. C. D.
2. 已知向量 , 是两个不共线的向量, , ,且 ,则 ( )
A. B. C. 1 D. 2
3. 将函数 的图象上所有的点向左平移 个单位长度,得到的图象所对应的函数的解析式为
( )
A. B. C. D.
4. 在 中, , , ,则 ( )
A. 9 B. 10 C. 12 D. 15
5. 为调查学生的体育达标情况,用简单随机抽样的方法,了解全校2506名学生的体育达标情况,抽取100
第1页/共5页
学科网(北京)股份有限公司名 学 生 作 为 样 本 , 第 个 ( , , , , ) 学 生 的 体 育 达 标 情 况 记 为 变 量 值
,则 表示的含义为( )
A. 全校学生体育达标的人数 B. 样本学生体育达标的人数
C. 全校学生体育达标率 D. 全校学生体育达标率的估计值
6. 已知 中, 是 的中点,且 , ,则 ( )
.
A B. C. D.
7. 如图,等边三角形与直线 在同一平面, 垂直 于 , ,则 绕 旋转一周形成的面所
围成的几何体的表面积是( )
.
A B. C. D.
8. 已知 , ,则 的最小值为( )
A. 1 B. C. 2 D. 4
二、选择题:本题共3小题,每小题6分,共18分,在每小题给出的选项中,有多项符合题
目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 已知复数 ,则( )
A. 的虚部为 B.
第2页/共5页
学科网(北京)股份有限公司的
C. D. 在复平面内对应 点位于第二象限
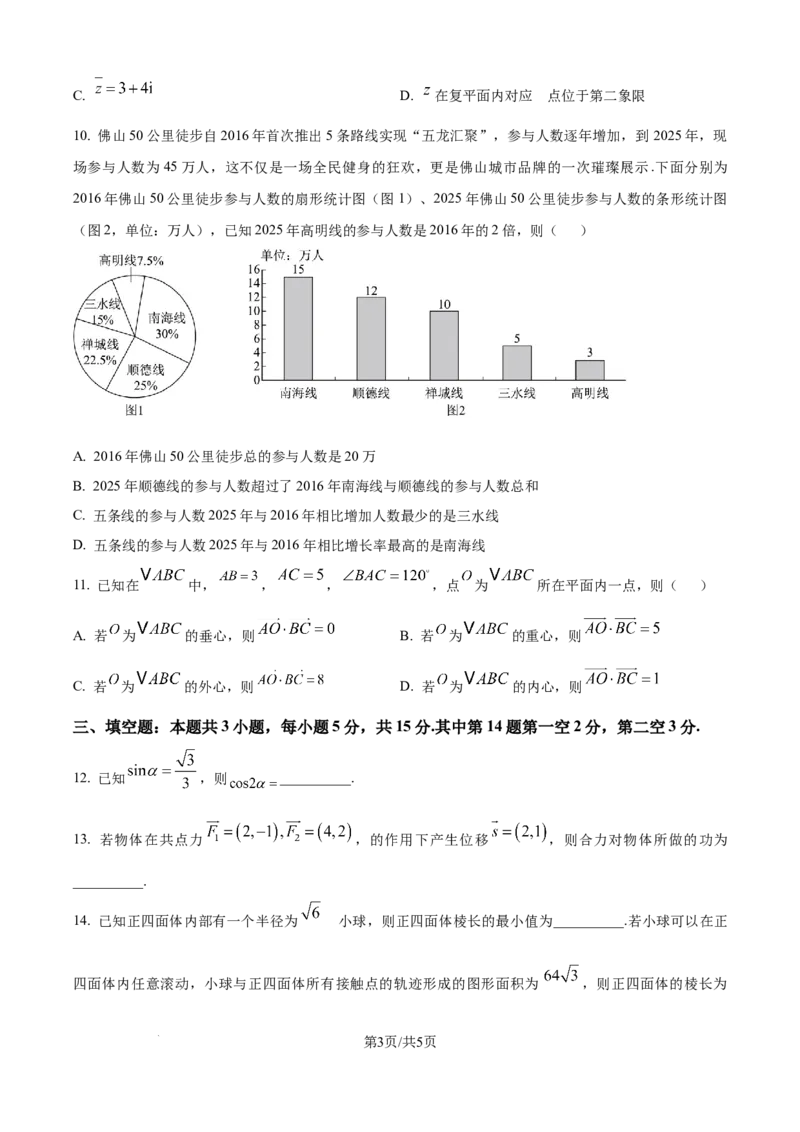
10. 佛山50公里徒步自2016年首次推出5条路线实现“五龙汇聚”,参与人数逐年增加,到 2025年,现
场参与人数为45万人,这不仅是一场全民健身的狂欢,更是佛山城市品牌的一次璀璨展示.下面分别为
2016年佛山50公里徒步参与人数的扇形统计图(图1)、2025年佛山50公里徒步参与人数的条形统计图
(图2,单位:万人),已知2025年高明线的参与人数是2016年的2倍,则( )
A. 2016年佛山50公里徒步总的参与人数是20万
B. 2025年顺德线的参与人数超过了2016年南海线与顺德线的参与人数总和
C. 五条线的参与人数2025年与2016年相比增加人数最少的是三水线
D. 五条线的参与人数2025年与2016年相比增长率最高的是南海线
11. 已知在 中, , , ,点 为 所在平面内一点,则( )
A. 若 为 的垂心,则 B. 若 为 的重心,则
C. 若 为 的外心,则 D. 若 为 的内心,则
三、填空题:本题共3小题,每小题5分,共15分.其中第14题第一空2分,第二空3分.
12. 已知 ,则 __________.
13. 若物体在共点力 ,的作用下产生位移 ,则合力对物体所做的功为
__________.
的
14. 已知正四面体内部有一个半径为 小球,则正四面体棱长的最小值为__________.若小球可以在正
四面体内任意滚动,小球与正四面体所有接触点的轨迹形成的图形面积为 ,则正四面体的棱长为
第3页/共5页
学科网(北京)股份有限公司__________.
四、解答题:本题共5小题,共77分,解答应写出文字说明、证明过程或演算步骤.
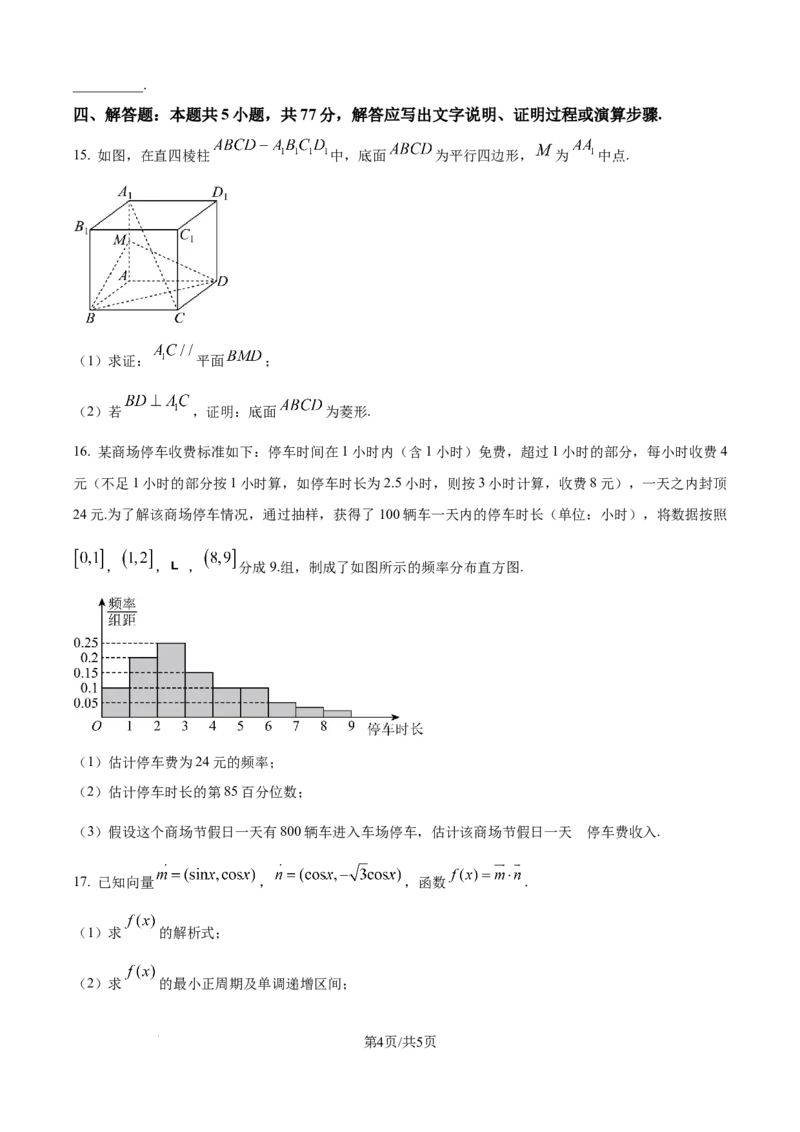
15. 如图,在直四棱柱 中,底面 为平行四边形, 为 中点.
(1)求证: 平面 ;
(2)若 ,证明:底面 为菱形.
16. 某商场停车收费标准如下:停车时间在1小时内(含1小时)免费,超过1小时的部分,每小时收费4
元(不足1小时的部分按1小时算,如停车时长为2.5小时,则按3小时计算,收费8元),一天之内封顶
24元.为了解该商场停车情况,通过抽样,获得了100辆车一天内的停车时长(单位:小时),将数据按照
, , , 分成9.组,制成了如图所示的频率分布直方图.
(1)估计停车费为24元的频率;
(2)估计停车时长的第85百分位数;
的
(3)假设这个商场节假日一天有800辆车进入车场停车,估计该商场节假日一天 停车费收入.
17. 已知向量 , ,函数 .
(1)求 的解析式;
(2)求 的最小正周期及单调递增区间;
第4页/共5页
学科网(北京)股份有限公司(3)若 在区间 上的值域为 ,求实数 的取值范围.
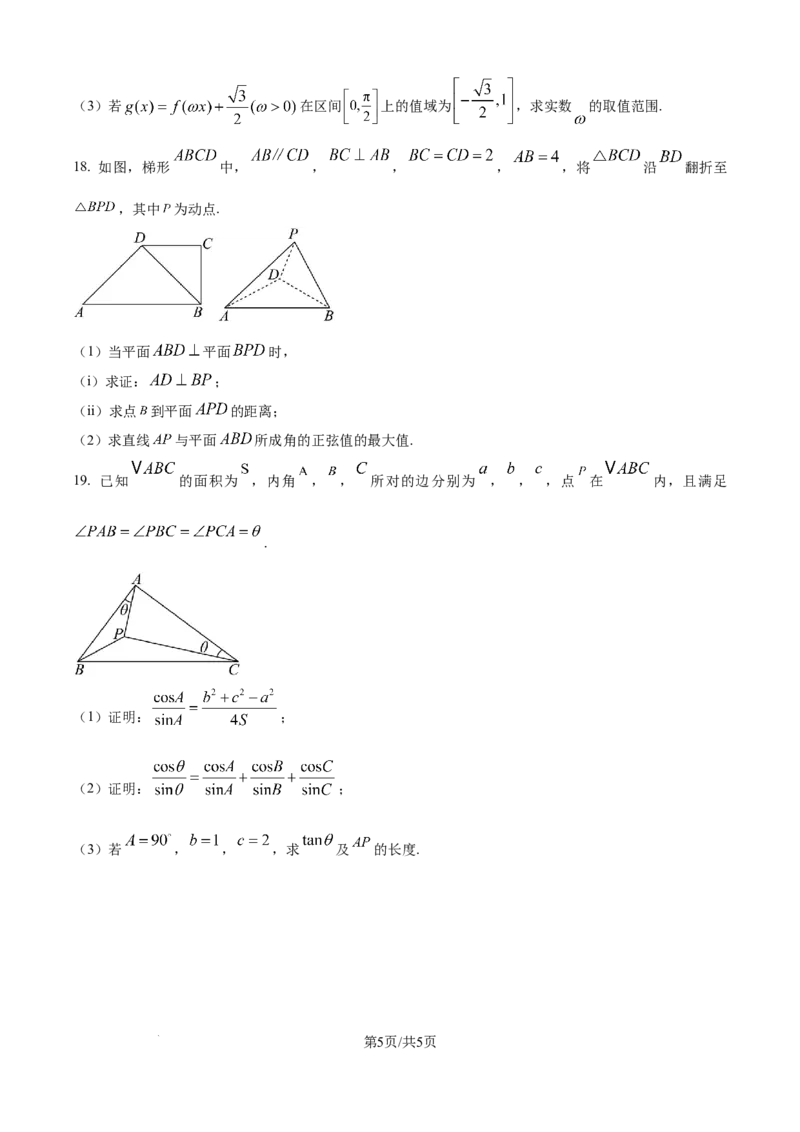
18. 如图,梯形 中, , , , ,将 沿 翻折至
,其中 为动点.
(1)当平面 平面 时,
(i)求证: ;
(ii)求点 到平面 的距离;
(2)求直线 与平面 所成角的正弦值的最大值.
19. 已知 的面积为 ,内角 , , 所对的边分别为 , , ,点 在 内,且满足
.
(1)证明: ;
(2)证明: ;
(3)若 , , ,求 及 的长度.
第5页/共5页
学科网(北京)股份有限公司