文档内容
人教 A 版 2019 必修第二册 期末测试卷 03
高一数学
满分:150分 时间:120分钟
一、单项选择题(5分×12题=60分)
1.已知平行四边形OABC中,O为坐标原点,A(2,2),C(1,-2)则⃗OB·⃗AC=( )
A.-6 B. -3 C. 3 D. 6
4-3i
2.设i是虚数单位,则复数 =( )
i
A.-3+4i B. 3-4i C.3+4i D.-3-4i
3.数据a ,a ,a ,…,a 的方差为σ2,则数据2a ,2a ,2a ,…,2a 的方差为( )
1 2 3 n 1 2 3 n
σ2
A. B. σ2 C.2σ2 D. 4σ2
2
4.在平行四边形ABCD中,AC为一条对角线,⃗AB=(2,4),⃗AC=(1,3),则⃗DA=( )
A. (2,4) B.(3,5) C. (1,1) D.(-1,-1)
5.从1,2,3,4这4个数中,不放回地任取两个数,两个数都是偶数的概率是(
)
1 1 1 1
A. B. C. D.
6 4 3 2
π
6.在△ABC 中,内角 A,B,C 所对的边分别是a,b,c,若c2=(a-b) 2+6,∠C= ,则
3
△ABC的面积是( )
9❑√3 3❑√3
A. 3 B. C. D. 3❑√3
2 2
7.已知点O是边长为2的正三角形ABC的重心,则⃗OB·⃗OC=( )
1 2 1 5
A.- B.- C.- D. -
6 3 2 6
8.演讲比赛共有 9 位评委分别给出某选手的原始评分,评定该选手的成绩时,
从9个原始评分中去掉一个最高分,去掉一个最低分,得到 7个有效分.7个有
效分和9个原始分相比,不变的数字特征是( )
A. 中位数 B. 平均数 C. 方差 D. 极差
1 sinC
9. 在△ABC中,内角A,B,C所对的边分别是a,b,c,若cosB= , =2,且
4 sinA❑√15
S = ,则b=( )
△ABC 4
A.4 B.3 C.2 D.1
10.设m,n是两条不同的直线,α,β是两个不同的页面,则下列结论正确的是
( )
A.若α//β,m⊂α,n⊂β,则m//n
B.若m//n,m//α,则n//α
C.若m⊂α,n⊂β,则m,n是异面直线
D.若m⊥α,n⊥α,则m//n
11.一个底面边长为3的正三棱锥的体积与表面积为24的正方体的体积相等,则
该正三棱锥的高( )
32❑√3 32❑√3
A. 12❑√3 B. C. D. 12
3 9
12.(多选)空气质量指数 AQI 是反映空气状况的指数,AQI 数值越小,表明空气
质量越好,其对应关系如下表所示:
AQI指数 0~50 51~100 101~150 151~200 201~300 >300
空气质量 优 良 轻度污染 中度污染 重度污染 严重污染
如图是某市10月1日~20日AQI指数变化趋势——
下列叙述正确的是( )
A.这20天中AQI指数值的中位数略高于100
1
B.这20天中的中度污染及以上的天数占
4
C.该市10月的前半个月的空气质量越来越好
D.总体来说,该市10月上旬的空气质量比中旬的空气质量好
二、填空题(5分×4题=20分)
13.已知复数z =1+2i,z +z =2+i,则z ·z =_________.
1 1 2 1 214.已知向量a,b满足(a+2b)·(a-b)=-8,且|a|=1,|b|=2,则a与b的夹角为 ________.
15.在数学考试中,甲的成绩在 90 分以上的概率是 0.15,在 80~89 分的概率为
0.45,在 70~79 分的概率为 0.25,那么甲在考试中取得 70 分以上成绩的概率
是________.
16.已知四棱锥 P-ABCD 的底面 ABCD 是矩形,其中 AD=2,AB=4,平面 PAD⊥平面
2❑√5
ABCD,PA=PD,且直线 PB 与 CD 所成角的余弦值为 ,则四棱锥 P-ABCD 的外
5
接球表面积为________.
三、解答题(6大题,共70分)
17.(10分)
1
已知非零向量a与b满足|a|=1,且(a-b)·(a+b)= .
2
1
(1)求a·b= ,求向量a,b的夹角.
2
(2)在(1)的条件下,求|a-2b|的值.
18.(12分)在△ABC中,内角A,B,C所对的边分别是a,b,c,
❑√3
且a=b cosC+ c sinB
3
(1)求角B的大小.
(2)若2b=a+c,试判断△ABC的形状并加以证明.
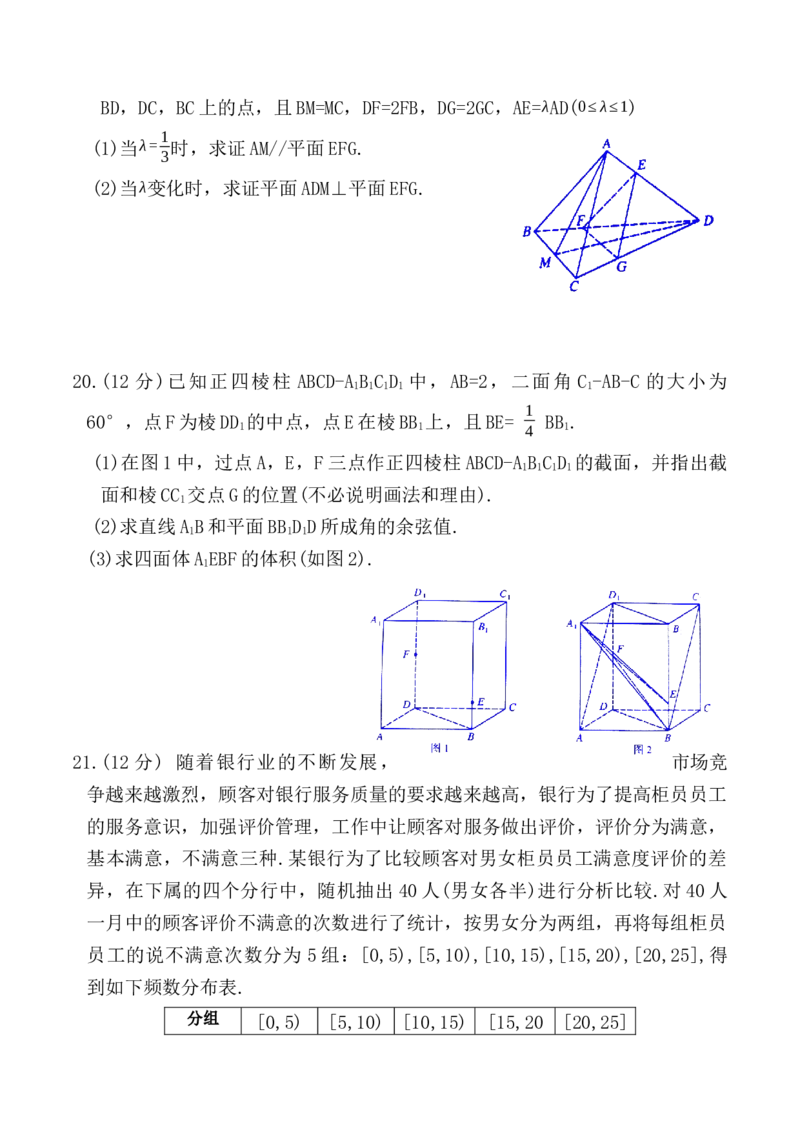
19.(12 分)已知在四面体 A-BCD 中,AB=AC,DB=DC,点 E,F,G,M 分别为 AD,BD,DC,BC上的点,且BM=MC,DF=2FB,DG=2GC,AE=λAD(0≤λ≤1)
1
(1)当λ= 时,求证AM//平面EFG.
3
(2)当λ变化时,求证平面ADM⊥平面EFG.
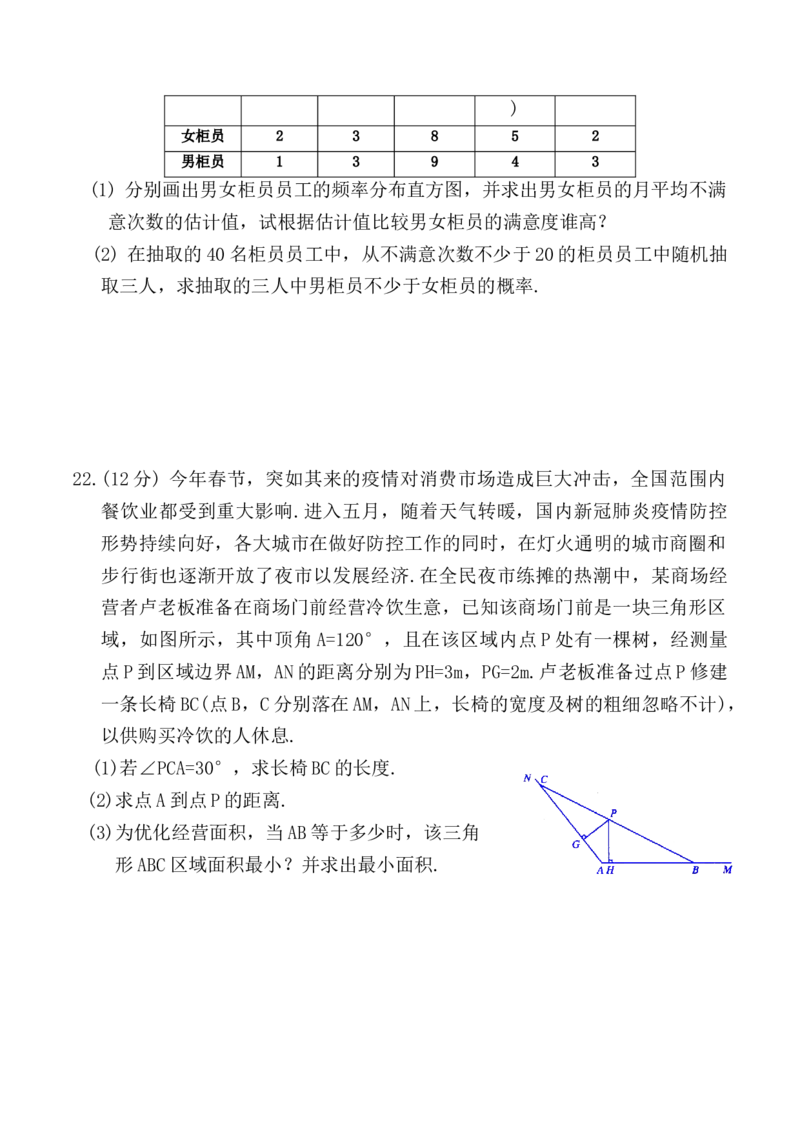
20.(12 分)已知正四棱柱 ABCD-A B C D 中,AB=2,二面角 C -AB-C 的大小为
1 1 1 1 1
1
60°,点F为棱DD 的中点,点E在棱BB 上,且BE= BB .
1 1 4 1
(1)在图 1 中,过点 A,E,F 三点作正四棱柱 ABCD-A B C D 的截面,并指出截
1 1 1 1
面和棱CC 交点G的位置(不必说明画法和理由).
1
(2)求直线A B和平面BB D D所成角的余弦值.
1 1 1
(3)求四面体A EBF的体积(如图2).
1
21.(12 分) 随着银行业的不断发展, 市场竞
争越来越激烈,顾客对银行服务质量的要求越来越高,银行为了提高柜员员工
的服务意识,加强评价管理,工作中让顾客对服务做出评价,评价分为满意,
基本满意,不满意三种.某银行为了比较顾客对男女柜员员工满意度评价的差
异,在下属的四个分行中,随机抽出 40 人(男女各半)进行分析比较.对 40 人
一月中的顾客评价不满意的次数进行了统计,按男女分为两组,再将每组柜员
员工的说不满意次数分为 5 组:[0,5),[5,10),[10,15),[15,20),[20,25],得
到如下频数分布表.
分组 [0,5) [5,10) [10,15) [15,20 [20,25])
女柜员 2 3 8 5 2
男柜员 1 3 9 4 3
(1) 分别画出男女柜员员工的频率分布直方图,并求出男女柜员的月平均不满
意次数的估计值,试根据估计值比较男女柜员的满意度谁高?
(2) 在抽取的40名柜员员工中,从不满意次数不少于 20的柜员员工中随机抽
取三人,求抽取的三人中男柜员不少于女柜员的概率.
22.(12 分) 今年春节,突如其来的疫情对消费市场造成巨大冲击,全国范围内
餐饮业都受到重大影响.进入五月,随着天气转暖,国内新冠肺炎疫情防控
形势持续向好,各大城市在做好防控工作的同时,在灯火通明的城市商圈和
步行街也逐渐开放了夜市以发展经济.在全民夜市练摊的热潮中,某商场经
营者卢老板准备在商场门前经营冷饮生意,已知该商场门前是一块三角形区
域,如图所示,其中顶角 A=120°,且在该区域内点 P 处有一棵树,经测量
点P到区域边界 AM,AN的距离分别为 PH=3m,PG=2m.卢老板准备过点 P修建
一条长椅 BC(点B,C分别落在 AM,AN上,长椅的宽度及树的粗细忽略不计),
以供购买冷饮的人休息.
(1)若∠PCA=30°,求长椅BC的长度.
(2)求点A到点P的距离.
(3)为优化经营面积,当AB等于多少时,该三角
形ABC区域面积最小?并求出最小面积.