文档内容
第一章 集合与常用逻辑用语
总分:120分时间:120分钟
一、单选题(总分48分,每题4分)
1.已知集合M={x|1≤x<3},N={1,2},则M∩N=( )
A. B. C. D.
【答案】B
【解析】∵ ,∴ .故选B.
2.下列元素与集合的关系表示正确的是( )
① N*;② ∉Z;③ ∈Q;④π∈Q
A.①② B.②③ C.①③ D.③④
【答案】B
【解析】① 不是正整数,∴ N*错误;② 是无理数,∴ 正确;
③ 是有理数,∴ 正确;④π是无理数,∴π∈Q错误;∴表示正确的为②③.
故选:B.
3.设命题 ,则 为( ).
A. B.
C. D.
【答案】C
【解析】命题 ,则 为: ,故选C.
4.已知全集U=R,集合M={x|-1≤x≤3},则∁U M=( )
A.{x|-13} D.{x|x≤-1或x≥3}
【答案】C【解析】由题意,全集 ,集合 ,所以 或 ,
故选C.
5. 是 的_________条件;( )
A.必要不充分 B.充要
C.充分不必要 D.既不充分也不必要
【答案】C
【解析】因为 ,但是 ,所以, 是 的充分不必要条件,
故选C。
6.设全集 , , ,则 ( )
A. B. C. D.
【答案】B
【解析】全集 , , ,
.故选B.
7.下列各式中,正确的个数是:① ;② ;③ ;
④ ;⑤ ;⑥ .
A.1 B.2 C.3 D.4
【答案】B
【解析】对①,集合与集合之间不能用 符号,故①不正确;
对②,由于集合两个集合相等,任何集合都是本身的子集,故②正确;
对③,空集是任何集合的子集,故③正确;
对④,空集是不含任何元素的集合,而 是含有1个元素的集合,故④不正确;
对⑤,集合 是数集,含有2个元素,集合 是点集,只含1个元素,故⑤不正确;
对⑥,元素与集合只能用 或 符号, 故⑥不正确.8.已知集合A={x|y ,x∈Z},则集合A的真子集个数为( )
A.32 B.4 C.5 D.31
【答案】D
【解析】因为 且 ,所以 ,故集合 的真子集个数为: .
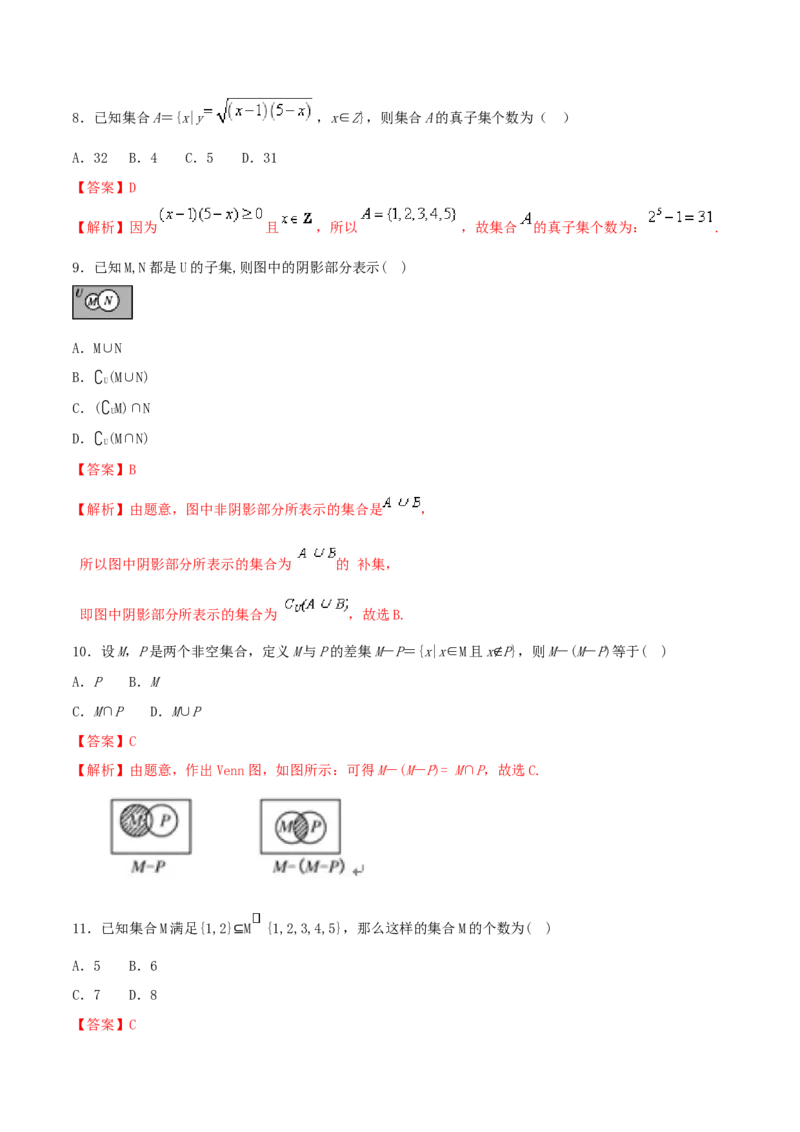
9.已知M,N都是U的子集,则图中的阴影部分表示( )
A.M∪N
B.∁U (M∪N)
C.(∁U M)∩N
D.∁U (M∩N)
【答案】B
【解析】由题意,图中非阴影部分所表示的集合是 ,
所以图中阴影部分所表示的集合为 的 补集,
即图中阴影部分所表示的集合为 ,故选B.
10.设M,P是两个非空集合,定义M与P的差集M-P={x|x∈M且x∉P},则M-(M-P)等于( )
A.P B.M
C.M∩P D.M∪P
【答案】C
【解析】由题意,作出Venn图,如图所示:可得M-(M-P)= M∩P,故选C.
11.已知集合M满足{1,2} M {1,2,3,4,5},那么这样的集合M的个数为( )
⊆
A.5 B.6
C.7 D.8
【答案】C【解析】根据题意,M集合一定含有元素1,2,且为集合{1,2,3,4,5}的真子集,所以集合M的个数为23-1
=7个,故选C.
12.对于实数 ,“ ”是“ ”的
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
【答案】B
【解析】主要考查不等式的性质.当c=0时显然左边无法推导出右边,但右边可以推出左边。
故选B.
二、填空题(总分16分,每题4分)
13.若 ,且 ,则 的可能取值组成的集合中元素的个数为_____.
【答案】3
【解析】当 时, ;当 ;
当 ;当 ,故 的可能取值组成的集合中元素的个数
为3.
14.已知集合 ,则A中元素的个数为_____.
【答案】9
【解析】法一:将满足 的整数 全部列举出来,即
,共有9个.
法二:根据集合 的元素特征及圆的方程,在坐标系中作出图形,如图所示,
易知在圆 中有9个整点,即为集合 的元素个数.15.已知集合 , ,且 ,则实数 的取值范围
是_________。
【答案】 .
【解析】由题意可得: ,
据此结合题意可得: ,即 ,
即实数 的取值范围是 .
16.有下列命题:
①“若 ,则 ”的否命题;
②“矩形的对角线相等”的否命题;
③“若 ,则 的解集是 ”的逆命题;
④“若 是无理数,则 是无理数”的逆否命题.
其中正确命题的序号是____________
【答案】①③④
【解析】对于①“若 ,则 ”的逆命题为“若 ,则 ”故逆命
题为真命题,则否命题也为真,故①正确;对于②“矩形的对角线相等”的逆命题为“对角线相等的四边
形是矩形”为假命题,故其逆命题也为假,故②错误;对于③其逆命题为:若
的解集是 ,则 ,当该不等式解集为 时,1. 时,不合题意,
2. 解得 ,故逆命题为真,即③正确;对于④,原命题为真,故逆否
命题也为真,故④正确,即正确的序号为①③④,故答案为①③④.
三、解答题(总分56分,17、18、19每题8分,20、21题10分,22每题12分.)
17.已知集合 , 或 .(1)若 ,求 ;
(2)若 ,求实数 的取值范围.
【答案】(1) ;(2) .
【解析】(1)当 时, , ,
所以 ;
(2)因为 ,所以 ,
解得: .
18.若A={3,5},B={x|x2+mx+n=0},A∪B=A,A∩B={5},求m,n的值.
【答案】
【解析】解:∵A∪B=A,A∩B={5},A={3,5},
∴B={5}.
∴方程x2+mx+n=0只有一个根为5,
∴
∴解得
19.已知全集 ,集合 , .
(1)求 ;
(2)若 ,求实数 的取值范围.
【答案】(1) ;(2) 的取值范围是
【解析】(1)∵ 或 , ,∴ .
(2) ,
①当 即 时, ;
②当 即 时,要使 ,有 ∴
又 ,∴ ,∴ 的取值范围是 .
20.已知集合 , .
(1)当 时,求 , ;
(2)若 ,求实数a的取值范围.
【答案】(1) ;(2) .
【解析】(1)当 时, , ,
,
∴ , }.
(2)因为 ,
所以 或
解得 或 ,
所以a的取值范围是 .21.已知集合 ,集合 .
(1)当 时,求 ;
(2)设 ,若“ ”是“ ”的必要不充分条件,求实数 的取值范围.
【答案】(1) , ;(2)
【解析】(1)当 时, ,集合 ,
所以 .
(2)因为 ,所以 , ,
因为“ ”是“ ”的必要不充分条件,所以 ,
所以 解得: .
22.求证:方程 有两个同号且不相等的实根的充要条件是 .
【答案】证明见解析.
【解析】证明:(1)先证充分性:
因为 ,
所以方程 的判别式 ,且两根积为 ,
所以方程 有两个同号且不相等的实根;
(2)再证必要性:
若方程 有两个同号且不相等的实根,设两根为 ,
则有 ,解得 ,
综合(1)(2)可知,方程 有两个同号且不相等的实根的充要条件是 ,命题得
证.