文档内容
2024 年普通高等学校招生全国统一考试(模拟)
注意事项:
1.答卷前,考生务必将自己的考生号、姓名、考点学校、考场号及座位号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.
如需要改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.
写在本试卷上无效.
3考试结束后,将本试卷和答题卡一并交回.
一、选择题:本题共 8小题,每小题 5分,共 40分.在每小题给出的四个选项中,只有一项是符
合题目要求的.
1
1.已知向量a =( 3,m ) ,b = −1, ,若a∥ b ,则m=( )
3
A.1 B.-1 C.9 D.-9
2.已知等差数列 { a } 的前n项和为S ,若a +a =1,则S =( )
n n 15 2010 2024
A.1012 B.1013 C.2024 D.2025
3.若虚数单位i是关于x的方程ax3 +bx2 +bx+1=0 ( a,b∈R ) 的一个根,则 a+bi =( )
A.0 B.1 C. 2 D.2
1
4.长时间玩手机可能影响视力,据调查,某学校学生中,大约有 的学生每天玩手机超过1h,这些人近视率
5
1 3
约为 ,其余学生的近视率约为 ,现从该校任意调查一名学生,他近视的概率大约是( )
2 8
1 7 2 7
A. B. C. D.
5 16 5 8
2 3 4 10
x x x x
5. +1 + +1 + +1 ++ +1 的展开式中含x项的系数为( )
2 3 4 10
A.9 B.10 C.18 D.20
1,x>0
6.已知函数sgn(x)= 0,x=0 ,则“sgn ( ex −1 ) +sgn (−x+1 )=0”是“x>1”的.( )
−1,x<0
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
7.在同一平面上有相距14公里的A,B两座炮台,A在B的正东方.某次演习时,A向西偏北θ方向发射炮
弹,B则向东偏北θ方向发射炮弹,其中θ为锐角,观测回报两炮弹皆命中18公里外的同一目标,接着A
学学科科网网((北北京京))股股份份有有限限公公司司θ
改向向西偏北 方向发射炮弹,弹着点为18公里外的点M ,则B炮台与弹着点M 的距离为( )
2
A.7公里 B.8公里 C.9公里 D.10公里
8.将1到30这30个正整数分成甲、乙两组,每组各15个数,使得甲组的中位数比乙组的中位数小2,则不同
的分组方法数是( )
A.2 ( C7 )2 B.2C7C7 C.2C6C7 D.2 ( C7 )2
13 13 14 14 14 14
二、多选题:本题共 3小题,每小题 6分,共 18分.在每小题给出的选项中,有多项符合题目要
求.全部选对的得 6分,部分选对的得部分分,有选错的得 0分.
2
9.已知函数 f ( x )= +a ( a∈R ),则( )
2x −1
A. f
(
x
)
的定义域为
(−∞,0 )∪( 0,+∞)
( )
B. f x 的值域为R
( )
C.当a=1时, f x 为奇函数
D.当a =2时, f
(−x )+
f
(
x
)=2
10.下列结论正确的是( )
A.一组样本数据的散点图中,若所有样本点 ( x ,y ) 都在直线y =0.95x+1上,则这组样本数据的样本相关
i i
系数为0.95
B.已知随机变量ξ∼ N ( 3,4 ) ,若ξ=2η+1,则D (η)=1
C.在2×2列联表中,若每个数据a,b,c,d 均变成原来的2倍,则χ2也变成原来的2倍
n(ad −bc)2
(χ2 = ,其中n=a+b+c+d )
( a+b )( c+d )( a+c )( b+d )
D.分别抛掷2枚质地均匀的骰子,若事件A=“第一枚骰子正面向上的点数是奇数”,B=“2枚骰子正面向上
的点数相同”,则A,B互为独立事件
11.已知圆C:x2 + y2 −10x+13=0,抛物线W : y2 =4x的焦点为F,P为W 上一点( )
A.存在点P,使PFC为等边三角形
B.若Q为C上一点,则 PQ 最小值为1
C.若 PC =4,则直线PF 与C相切
D.若以PF 为直径的圆与C相外切,则 PF =22−12 3
学学科科网网((北北京京))股股份份有有限限公公司司三、填空题:本题共 3小题,每小题 5分,共 15分.
1
12.集合A={x∣lgx<1},B=x >1,则A∩ B =__________.
x R
x2 y2 ( )
13.已知F,F 是双曲线C: − =1(a >0,b>0)的左、右焦点,点P 3t,t (t >0)在C上.
1 2 a2 b2
tan∠FF P=2+ 3,则C的离心率为__________.
1 2
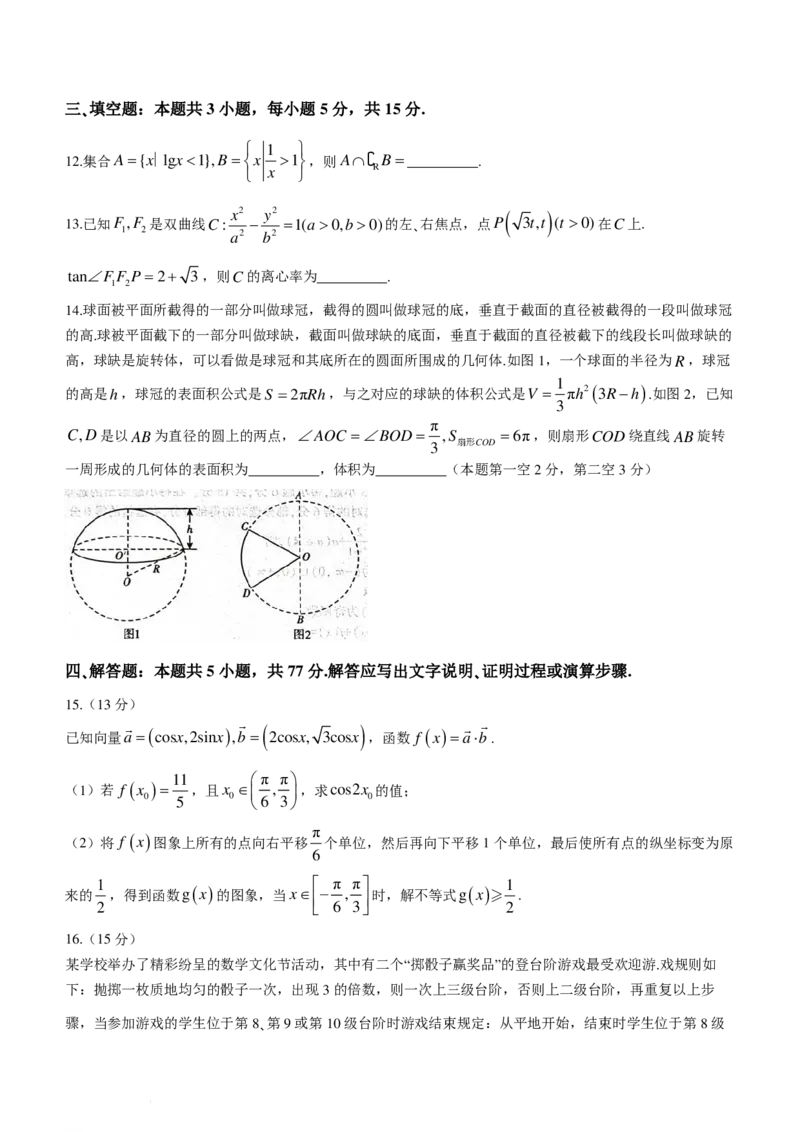
14.球面被平面所截得的一部分叫做球冠,截得的圆叫做球冠的底,垂直于截面的直径被截得的一段叫做球冠
的高.球被平面截下的一部分叫做球缺,截面叫做球缺的底面,垂直于截面的直径被截下的线段长叫做球缺的
高,球缺是旋转体,可以看做是球冠和其底所在的圆面所围成的几何体.如图1,一个球面的半径为R,球冠
1
的高是h,球冠的表面积公式是S =2πRh,与之对应的球缺的体积公式是V = πh2( 3R−h ) .如图2,已知
3
π
C,D是以AB为直径的圆上的两点,∠AOC =∠BOD= ,S =6π,则扇形COD绕直线AB旋转
3
扇形COD
一周形成的几何体的表面积为__________,体积为__________(本题第一空2分,第二空3分)
四、解答题:本题共 5小题,共 77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)
( )
已知向量a =( cosx,2sinx ) ,b = 2cosx, 3cosx ,函数 f ( x )=a⋅b.
11 π π
(1)若 f ( x )= ,且x ∈ , ,求cos2x 的值;
0 5 0 6 3 0
π
( )
(2)将 f x 图象上所有的点向右平移 个单位,然后再向下平移1个单位,最后使所有点的纵坐标变为原
6
1 π π 1
来的 ,得到函数g ( x ) 的图象,当x∈ − , 时,解不等式g ( x ) .
2 6 3 2
16.(15分)
某学校举办了精彩纷呈的数学文化节活动,其中有二个“掷骰子赢奖品”的登台阶游戏最受欢迎游.戏规则如
下:抛掷一枚质地均匀的骰子一次,出现3的倍数,则一次上三级台阶,否则上二级台阶,再重复以上步
骤,当参加游戏的学生位于第8、第9或第10级台阶时游戏结束规定:从平地开始,结束时学生位于第8级
学学科科网网((北北京京))股股份份有有限限公公司司台阶可获得一本课外读物,位于第9级台阶可获得一套智力玩具,位于第10级台阶则认定游戏失败.,
(1)某学生抛掷三次骰子后,按游戏规则位于第X 级台阶,求X 的分布列及数学期望E(X);
(2)甲、乙两位学生参加游戏,求恰有一人获得奖品的概率;
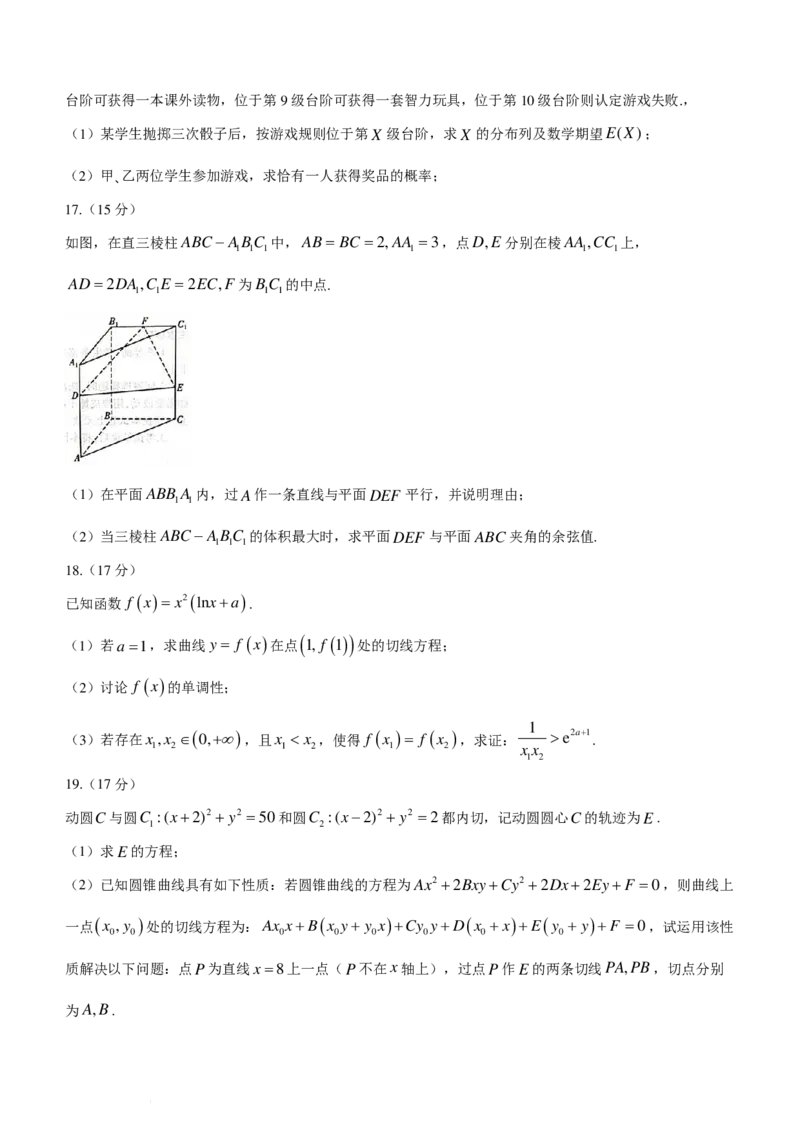
17.(15分)
如图,在直三棱柱ABC−ABC 中,AB= BC =2,AA =3,点D,E分别在棱AA,CC 上,
1 1 1 1 1 1
AD=2DA,C E =2EC,F为BC 的中点.
1 1 1 1
(1)在平面ABB A 内,过A作一条直线与平面DEF 平行,并说明理由;
1 1
(2)当三棱柱ABC−ABC 的体积最大时,求平面DEF 与平面ABC夹角的余弦值.
1 1 1
18.(17分)
已知函数 f ( x )= x2( lnx+a ) .
(1)若a=1,求曲线y = f ( x ) 在点 ( 1, f ( 1 )) 处的切线方程;
( )
(2)讨论 f x 的单调性;
1
(3)若存在x ,x ∈( 0,+∞) ,且x < x ,使得 f ( x )= f ( x ) ,求证: >e2a+1 .
1 2 1 2 1 2 x x
1 2
19.(17分)
动圆C与圆C :(x+2)2 + y2 =50和圆C :(x−2)2 + y2 =2都内切,记动圆圆心C的轨迹为E.
1 2
(1)求E的方程;
(2)已知圆锥曲线具有如下性质:若圆锥曲线的方程为Ax2 +2Bxy+Cy2 +2Dx+2Ey+F =0,则曲线上
一点 ( x ,y ) 处的切线方程为:Ax x+B ( x y+ y x )+Cy y+D ( x +x )+E ( y + y )+F =0,试运用该性
0 0 0 0 0 0 0 0
质解决以下问题:点P为直线x=8上一点(P不在x轴上),过点P作E的两条切线PA,PB,切点分别
为A,B.
学学科科网网((北北京京))股股份份有有限限公公司司(i)证明:直线AB过定点;
(ii)点A关于x轴的对称点为A′,连接A′B交x轴于点M ,设AC M,BC M 的面积分别为S ,S ,求
2 2 1 2
S −S 的最大值.
1 2
学学科科网网((北北京京))股股份份有有限限公公司司