文档内容
A级:“四基”巩固训练
一、选择题
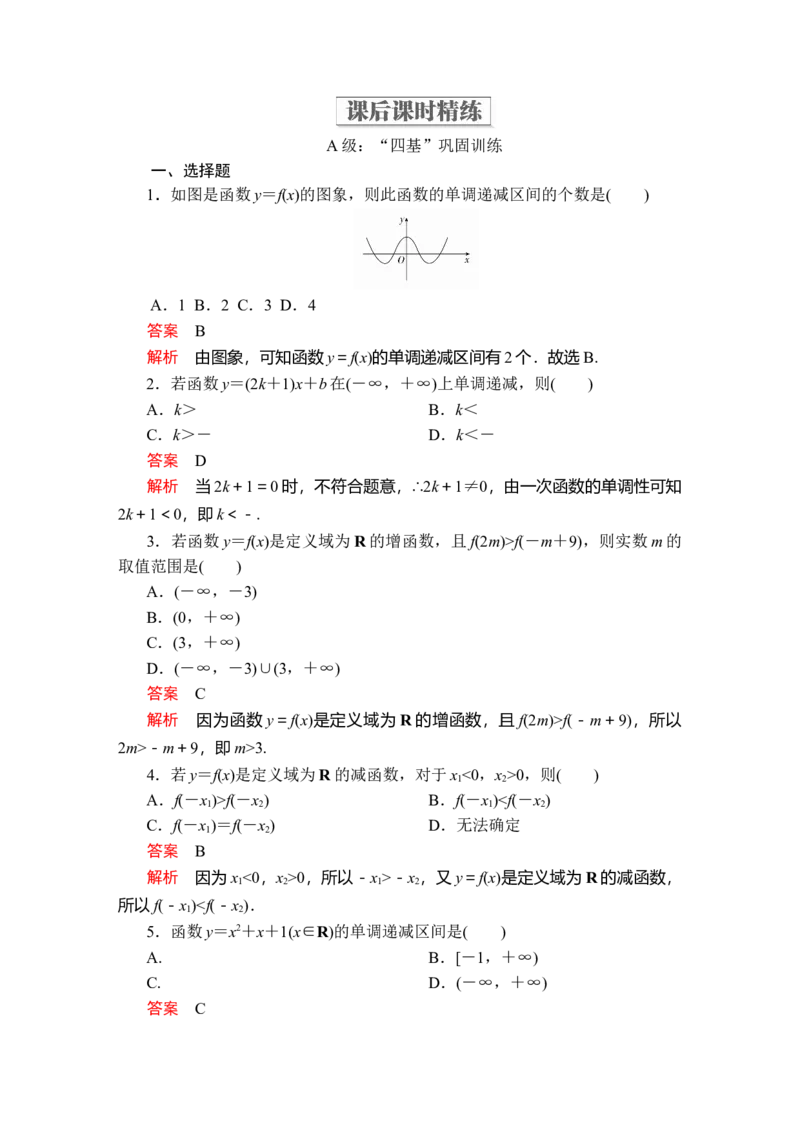
1.如图是函数y=f(x)的图象,则此函数的单调递减区间的个数是( )
A.1 B.2 C.3 D.4
答案 B
解析 由图象,可知函数y=f(x)的单调递减区间有2个.故选B.
2.若函数y=(2k+1)x+b在(-∞,+∞)上单调递减,则( )
A.k> B.k<
C.k>- D.k<-
答案 D
解析 当2k+1=0时,不符合题意,∴2k+1≠0,由一次函数的单调性可知
2k+1<0,即k<-.
3.若函数y=f(x)是定义域为R的增函数,且f(2m)>f(-m+9),则实数m的
取值范围是( )
A.(-∞,-3)
B.(0,+∞)
C.(3,+∞)
D.(-∞,-3)∪(3,+∞)
答案 C
解析 因为函数y=f(x)是定义域为 R的增函数,且 f(2m)>f(-m+9),所以
2m>-m+9,即m>3.
4.若y=f(x)是定义域为R的减函数,对于x <0,x >0,则( )
1 2
A.f(-x )>f(-x ) B.f(-x )0,所以-x >-x ,又y=f(x)是定义域为R的减函数,
1 2 1 2
所以f(-x )0,则f(-3)与
1 2 1 2 1 2
f(-π)的大小关系是______.
答案 f(-3)>f(-π)
解析 由(x -x )[f(x )-f(x )]>0,可知函数f(x)为增函数.又-3>-π,所以
1 2 1 2
f(-3)>f(-π).
8.已知函数f(x)=是定义域为R的减函数,则实数a的取值范围是________.
答案 (0,2]
解析 依题意得实数a应满足
解得00,2+x>0,
1 2 2 1
∴f(x )-f(x )>0,∴f(x )>f(x ),
1 2 1 2
∴函数f(x)=-x3+1是减函数.
10.已知函数y=f(x)在[0,+∞)上单调递减,试比较f与f(a2-a+1)的大小.
解 ∵a2-a+1=2+≥,
∴与a2-a+1都在区间[0,+∞)内.
又∵y=f(x)在区间[0,+∞)上单调递减,
∴f≥f(a2-a+1).
B级:“四能”提升训练
1.已知函数f(x)=
(1)画出f(x)的图象;
(2)写出f(x)的单调递增区间及值域.
解 (1)f(x)的图象如下图.(2)由图象和解析式可知,函数 f(x)的单调递增区间为[-1,0]和[2,5],其值域
为[-1,3].
2.已知函数f(x),∀x,y∈R,总有f(x+y)=f(x)+f(y)-1,并且当x>0时,
f(x)>1.
(1)求证:f(x)在R上单调递增;
(2)若f(4)=5,求解不等式f(3m2-m-2)<3.
解 (1)证明:∀x ,x ∈R,且x 0,所以f(x -x )>1.
2 1 2 1
故f(x )-f(x )<0,
1 2
即当x