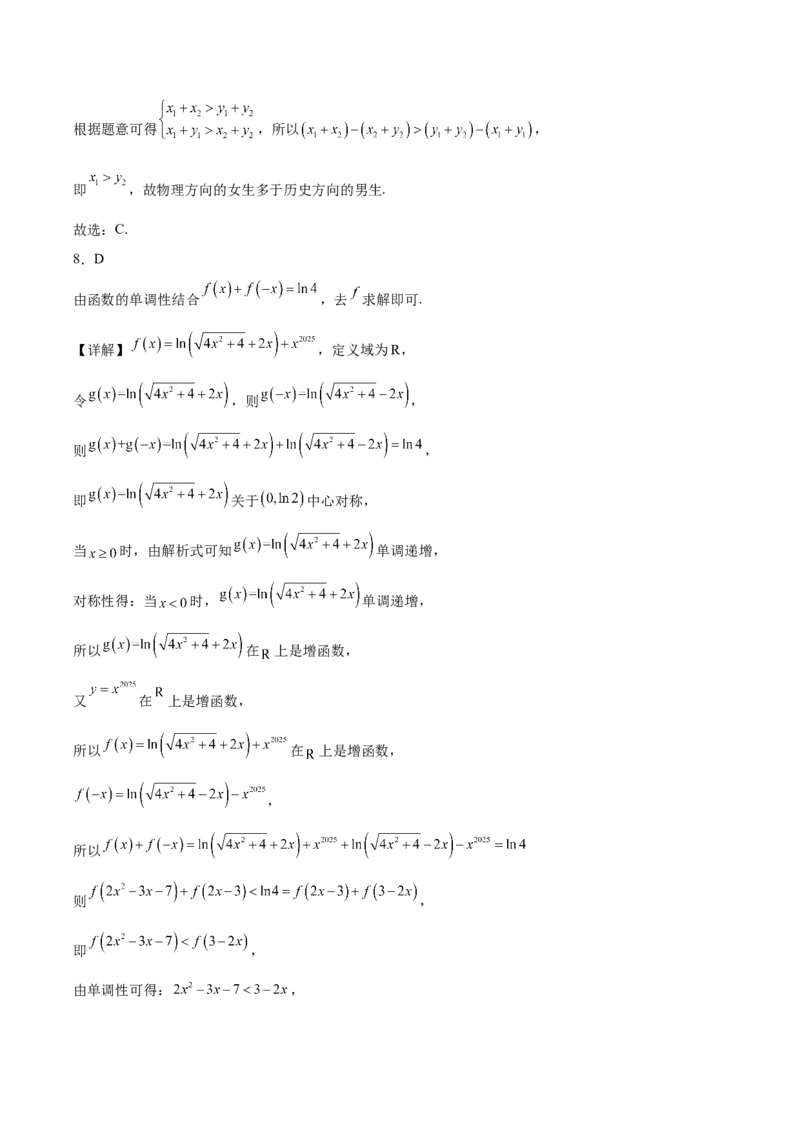文档内容
2025-2026学年高一上学期两校12月联考二
数学试题
一、单选题
1.命题“ ,有 ”的否定是( )
A. ,有 B. ,有
C. ,有 D. ,有
2.函数 的定义域为( )
A. B. C. D.
3.一元二次方程 有一个正实根和一个负实根的充分不必要条件是( )
A. B. C. D.
4.已知 ,则 ( )
A. B. C. D.
5.已知函数 的图象如下,则 的解析式可能为( )
A. B. C. D.
6.已知函数 ,且 ,则 的值为( )A.0 B.1 C. D.0或1
7.已知某校高一年级女生人数多于男生人数,在分科后选报物理方向的学生人数多于历史方向的学生人
数,则( )
A.物理方向的男生多于物理方向的女生
B.历史方向的女生多于历史方向的男生
C.物理方向的女生多于历史方向的男生
D.物理方向的男生多于历史方向的女生
8.已知函数 ,则不等式 的解集为( )
A. B.
C. D.
二、多选题
9.下列说法正确的是( )
A.若 终边上一点的坐标为 ,则
B.若角 为锐角,则 为钝角
C.若圆心角为 的扇形的弧长为 ,则该扇形的面积为
D.若 ,且 ,则
10.若 , ,且 ,则下列说法正确的有( )
A. 的最小值是
B. 的最大值是
C. 的最小值是
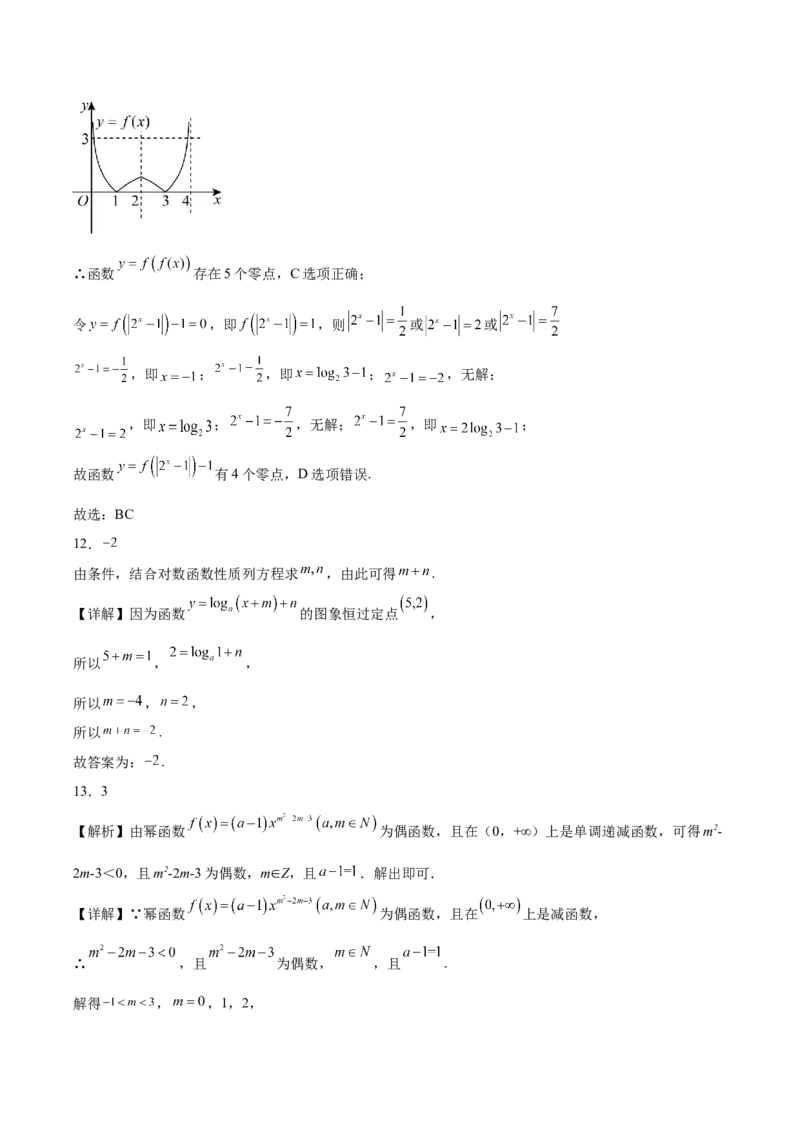
D. 的最小值是11.已知函数 的定义域为 , 为偶函数,当 时, ,则下列说
法正确的是( )
A.若函数 有四个零点 , , , ,则 的取值范围为
B.若函数 有四个零点 , , , ,则 的取值范围为
C.函数 的零点个数为5个
D.函数 的零点个数为6个
三、填空题
12.若函数 ( ,且 )的图象恒过定点 ,则 .
13.幂函数 为偶函数,且在 上是减函数,则 .
14.已知 ,函数 ,满足 ,则 ,若存在 ,
使得 ,则 的取值范围是 .
四、解答题
15.化简求值:
(1) ;
(2) .
16.已知集合 ,
(1)求集合 ;
(2)当 时,求 ;(3)若集合 ,求实数 的取值范围.
17.已知函数 ,若函数 在区间 上的最大值与最小值之和为 .
(1)求函数 解析式,并求出关于 的不等式 的解集;
(2)求函数 , 的值域,并求出取得最值时对应的 的值.
18.设函数 是定义在区间 上的函数,若对区间中的任意两个实数 ,都有
,则称 为区间上的下凸函数(即凹函数).
(1)已知 为下凸函数,若 ,求 最大值.
(2)求证:函数 在 是下凸函数(即凹函数).
(3)在 中,角A,B,C的对边分别为a,b,c,请试着用凹函数的这种性质证明下面的不等式:
.
19.已知函数 在某个区间上的单调性遵循“同增异减”的规律,具体如下:
内层函数 递增 递增 递减 递减
外层函数 递增 递减 递增 递减
复合函数 递增 递减 递减 递增
设函数 ( ,且 ).
(1)若 ,求 的值;
(2)若对于任意实数x, 恒成立,求实数m的取值范围;
(3)证明: . 若函数 满足 , ,函数 一定是偶函数吗?请说明理由.1.C
根据全称命题的否定是特称命题分析判断.
【详解】由题意可得:命题“ ,有 ”的否定是“ ,有 ”.
故选:C.
2.C
根据对数有意义、根式有意义列不等式求解即可.
【详解】因为函数 ,
所以 ,解之可得 ,
函数 的定义域为 .
故选:C.
3.C
求出方程有一个正实根和一个负实根的充要条件,结合选项,判断哪一个是该条件的真子集,即可得答案.
【详解】由题意知一元二次方程 的两根为 ,
要使得方程有一个正实根和一个负实根,需 ,
结合选项知,只有 ,
即一元二次方程 有一个正实根和一个负实根的充分不必要条件是 ,
故选:C
4.D
根据条件,利用“齐次式”,即可求解.
【详解】因为 ,则 ,
故选:D.
5.D
先由函数奇偶性排除AB,再由 时函数值正负情况可得解.【详解】由图可知函数为偶函数,而函数 和函数 为奇函数,故排除选项AB;
又当 时 ,此时 ,
由图可知当 时, ,故C不符合,D符合.
故选:D
6.B
根据分段函数解析式求出 的值,再代入计算可得.
【详解】因为 且 ,
所以 或 ,
解得 或 ,
当 时, ;
当 时, ;
综上可得 的值为 .
故选:B
7.C
根据已知条件,设分科后选报物理方向的女生数为 ,男生数为 ,选报历史方向的女生数为 ,男生数
为 ,根据题意可得 ,计算可得结论.
【详解】根据已知条件,设分科后选报物理方向的女生数为 ,男生数为 ,选报历史方向的女生数为 ,
男生数为 ,根据题意可得 ,所以 ,
即 ,故物理方向的女生多于历史方向的男生.
故选:C.
8.D
由函数的单调性结合 ,去 求解即可.
【详解】 ,定义域为R,
令 ,则 ,
则 ,
即 关于 中心对称,
当 时,由解析式可知 单调递增,
对称性得:当 时, 单调递增,
所以 在 上是增函数,
又 在 上是增函数,
所以 在 上是增函数,
,
所以
则 ,
即 ,
由单调性可得: ,解得: ,
所以不等式 的解集为 ,
故选:D
9.ACD
由终边上的点坐标及余弦函数的定义判断A;特殊角 判断B;应用扇形的弧长、面积公式判断C;
利用同角三角函数关系求已知角的正余弦值,进而求正切值判断D.
【详解】A,由 终边上的点 ,知 ,对;
B,由锐角 ,则 也是锐角,错;
C,设扇形半径为 ,根据弧长公式有弧长 ,则 ,
所以扇形面积为 ,对;
D,由题设 ,则 ,
又 ,则 ,结合 ,可得 ,
所以 ,对.
故选:ACD
10.ACD
利用基本不等式求最值,逐项判断即可.
【详解】对A:因为 ,即 (当且仅当 即 时取
“ ”),故A项正确;
对B:因为 (当且仅当 即 时取“ ”),
故B项错误;对C:因为 ,
所以 (当且仅当 即 时取“ ”),故C项正确;
对D:由 ,
所以 ,由B知: 成立,故D项正确.
故选:ACD
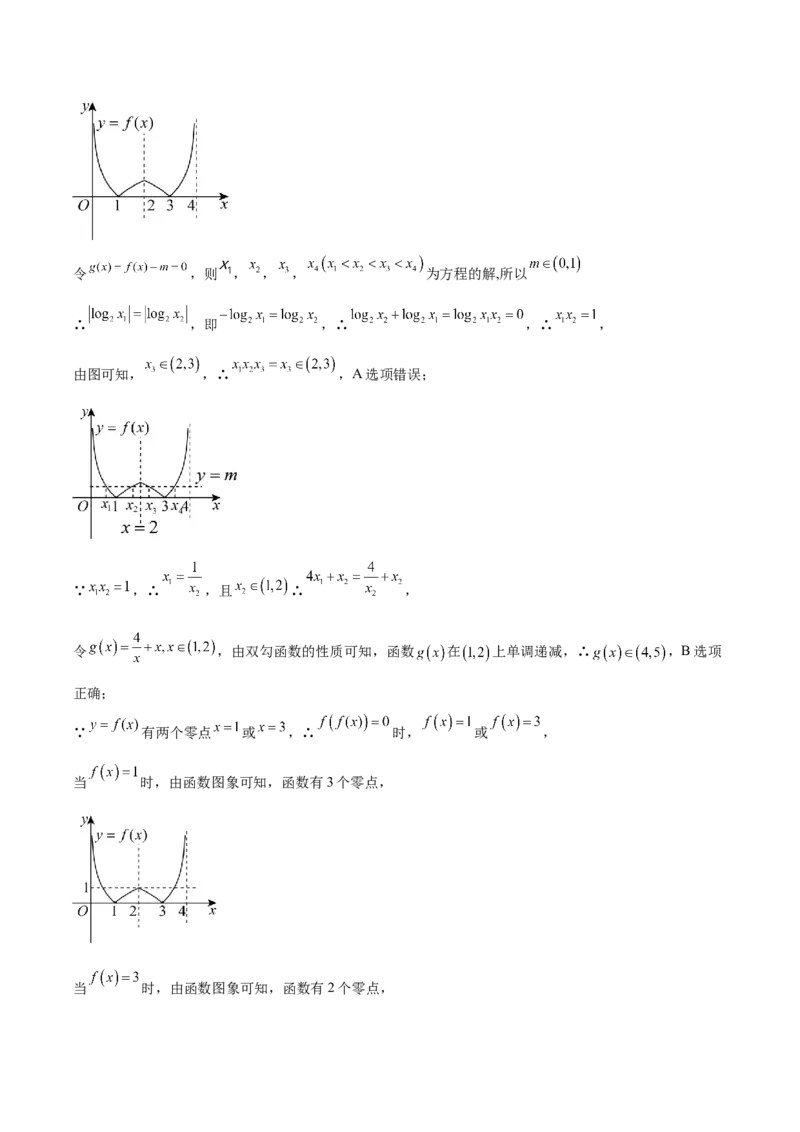
11.BC
由题意得到函数对称轴,作出函数大致图象.结合函数图象和对数的运算知函数 的零点 与 的关系,
且得到 的取值范围,即可判断A选项;由 与 的关系化简 ,利用 的范围及函数的单调性求
得 取值范围,判断B选项;由函数 的零点,得到 时 的值,然后分别由函
数图像知道对应零点个数,即可判断C选项;令 ,求得 的值,分别求解方程,即可
求得函数 的零点个数,判断D选项.
【详解】∵函数 为偶函数,即
则函数 关于 对称,
当 时, , ,
∴函数 的大致图像如下图,令 ,则 , , , 为方程的解,所以
∴ ,即 ,∴ ,∴ ,
由图可知, ,∴ ,A选项错误;
∵ ,∴ ,且 ∴ ,
令 ,由双勾函数的性质可知,函数 在 上单调递减,∴ ,B选项
正确;
∵ 有两个零点 或 ,∴ 时, 或 ,
当 时,由函数图象可知,函数有3个零点,
当 时,由函数图象可知,函数有2个零点,∴函数 存在5个零点,C选项正确;
令 ,即 ,则 或 或
,即 ; ,即 ; ,无解;
,即 ; ,无解; ,即 ;
故函数 有4个零点,D选项错误.
故选:BC
12.
由条件,结合对数函数性质列方程求 ,由此可得 .
【详解】因为函数 的图象恒过定点 ,
所以 , ,
所以 , ,
所以 .
故答案为: .
13.3
【解析】由幂函数 为偶函数,且在(0,+∞)上是单调递减函数,可得m2-
2m-3<0,且m2-2m-3为偶数,m∈Z,且 .解出即可.
【详解】∵幂函数 为偶函数,且在 上是减函数,
∴ ,且 为偶数, ,且 .
解得 , ,1,2,且 ,
只有 时满足 为偶数.
∴ .
故答案为:3.
14.
【详解】 ,得 ,
所以 ,
若 , ,得 ,
此时 ,
若 , ,此时 ,不成立,
若 , ,得 ,
此时 ,
设 , , 在区间 上单调递增, ,所以 的范围是
综上可知, 的取值范围是 .
故答案为:
15.(1)
(2)
(1)利用诱导公式化简求得正确答案.
(2)根据对数运算求得正确答案.【详解】(1)
.
(2)
.
16.(1)
(2)
(3) .
(1)通过确定函数 的值域求出集合 ;
(2)分别求出集合 ,进而求出 即可
(3)先将 转化为 ,再求出实数 的取值范围即可.
【详解】(1)因为 ,所以 ,即 ,
故 ;
(2)当 时, ,
故 ;
(3)因为 ,所以 ,又因为 ,故 ,
所以 ,
综上,实数 的取值范围是 .
17.(1) , 或 ;
(2) ,取最小值时 ,取最大值时 .
(1)根据给定条件,利用对数函数单调性求出最值列式求出 ,再利用单调性解不等式.
(2)由(1)的结论求出 并换元,转化为二次函数求解.
【详解】(1)函数 定义域为 ,且 在 上单调,
由函数 在区间 上的最大值与最小值之和为 ,
得 ,即 ,解得 ,
于是 ;
,
解 ,得 或 ;
解 ,即 ,得 或 ,
因此 或 ,
所以不等式 的解集 或 .
(2)由(1)知, ,
令 ,由 ,得 , ,
当 时, ,此时 ;当 时, ,此时 ,
所以函数 的值域为 ,取最小值时 ,取最大值时 .18.(1)4
(2)证明见解析
(3)证明见解析
(1)由凹函数的定义结合指数的运算求解即可;
(2)由凹函数的定义证明即可;
(3)由凹函数的定义结合基本不等式证明即可.
【详解】(1)由 为下凸函数,得
因此 ,当且仅当 时等号成立,则
即 ,所以 的最大值是4.
(2)
,
, ,
,
是 上的凹函数.
(3)因为幂函数 在 内是凹函数.
所以 ,即 ,当且仅当 时,等号成立.又因为幂函数 在 内是增函数,所以 .当且仅当 时,等号成立.
同理可证: ,当且仅当 时,等号成立.
,当且仅当 时,等号成立.
三式相加得: ,
又 ,
所以 当且仅当 时,等号成立.
不等式得证.
19.(1)47
(2)
(3)答案见解析
【详解】(1) ,∴ ,即 .
两边平方得 , .
(2)∵ 且定义域为R,
∴ 是定义在R上的偶函数,
∴由 ,得 .
设 , ,则 .
当 时, 在 上单调递增,∴ .
又 在 上单调递增,∴ 在 上单调递增.
当 时, 在 上单调递减, .
又 在 上单调递减,∴ 在 上单调递增.综上, 在 上单调递增,∴ 对 恒成立,
即不等式 恒成立,
整理得 对 恒成立,
∴结合一元二次方程根的判别式,得 且 ,
解得 ,即m的取值范围为 .
(3)证明:∵ ,
,
∴ .
令 ,则 ,∴ 或 .
当 时,令 ,则 ,即 ,
此时函数 是偶函数.
当 时,令 ,则 ,即 ,
此时函数 既是奇函数又是偶函数.