文档内容
2024 年高考第二次模拟考试
高三数学
参考答案
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选
项是符合题目要求的.
1 2 3 4 5 6 7 8
B D C B D B B D
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目
要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
9.ABD 10.ACD 11.BC
三、填空题:本题共4小题,每小题5分,共20分.
12.240 13. 0 14.2 3+2
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)【解析】
【小问1详解】
对于任意的n∈N*都有3S =2a +1,
n n
当n≥2时,3S =2a +1,两式相减得3 ( S −S )=( 2a +1 )−( 2a +1 ),即
n−1 n−1 n n−1 n n−1
3a =2a −2a ( n≥2 ) ,
n n n−1
进而得a =−2a ( n≥2 ) , .............................................4分
n n−1
当n=1时,3S =2a +1,故a =1,
1 1 1
{ }
所以数列 a 是以首项为1,公比为−2的等比数列,
n
所以a =(−2 )n−1 .............................................6分
n
【小问2详解】
当n为奇数时,a =2n−1,且a >0,当n为偶数时,a =−2n−1,且a <0,
n n n n
因此当n为大于1的奇数时, { a } 的前n项中的最大值为a =(−2 )n−1,最小值为a =(−2 )n−2,
n n n−1
M +m a +a
此时b = n n = n n−1 ,
n 2 2因此当n为偶数时, { a } 的前n项中的最大值为a =(−2 )n−2,
n n−1
最小值为a =(−2 )n−1,此时b = M n +m n = a n−1 +a n , .............................................10分
n n 2 2
当n=1时,b =a ,
1 1
{ }
因此 b 的前20项和
n
a +a a +a a +a
T =b +( b +b ++b )+( b +b +b ++b )=a + 3 2 + 5 4 ++ 19 18
20 1 3 5 19 2 4 6 20 1 2 2 2
a +a a +a a +a a S +S 1 S +S +a 1 (−2 )19
+ 1 2 + 3 4 ++ 19 20 = 1 + 19 20 = + 19 19 20 =S + +
2 2 2 2 2 2 2 19 2 2
1−(−2 )19 1 (−2 )19 5−219
= + + = .............................................13分
1+2 2 2 6
16.(15分)【解析】
【小问1详解】
设ξ表示1条灯带在安全使用寿命内更换的灯珠数量,
则P ( ξ =5 )=P ( ξ =7 )=P ( ξ =8 )=0.2,P ( ξ =6 )=0.4,
{ }
X的取值范围是 10,11,12,13,14,15,16 ,
P ( X =10 )=0.2×0.2=0.04,
P ( X =11 )=2×0.2×0.4=0.16,
P ( X =12 )=0.42 +2×0.2×0.2=0.24,
P ( X =13 )=2×( 0.2×0.2+0.2×0.4 )=0.24,
P ( X =14 )=0.22 +2×0.4×0.2=0.2,
P ( X =15 )=2×0.2×0.2=0.08,
P ( X =16 )=0.2×0.2=0.04,
X的分布列为
X 10 11 12 13 14 15 16
P 0.04 0.16 0.24 0.24 0.2 0.08 0.04
............................................. 6分
【小问2详解】由(1)可知P(X ≥12)=0.8,
P ( X ≥13 )=0.56,故n =13. .............................................9分
0
【小问3详解】
由(2)可知n=n −1=12.
0
在灯带安全使用寿命期内,当n=12时,设购买替换灯珠所需总费用为u元,当n =13时,设购买
替换灯珠所需总费用为v元,则E
(
u
)=24+0.24×4+0.2×8+0.08×12+0.04×16=28.16,
E
(
v
)=26+0.2×4+0.08×8+0.04×12=27.92.
E
(ν)<
E
(
u
)
,
故以购买替换灯珠所需总费用的期望值为依据,n=n 比n=n −1的方案更优。 ................... 13分
0 0
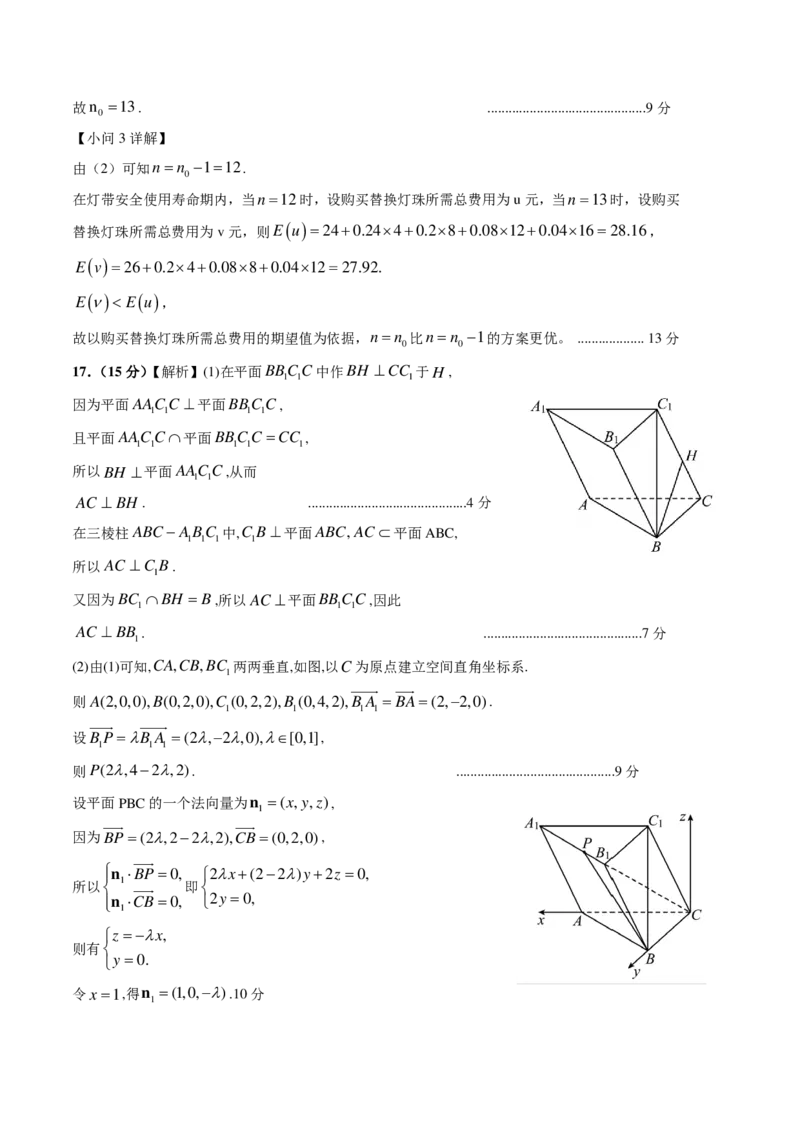
17.(15分)【解析】(1)在平面BBCC中作BH ⊥CC 于H ,
1 1 1
因为平面AACC ⊥平面BBCC,
1 1 1 1
且平面AACC∩平面BBCC =CC ,
1 1 1 1 1
所以BH ⊥平面AACC,从而
1 1
AC ⊥ BH . .............................................4分
在三棱柱ABC−ABC 中,C B⊥平面ABC,AC ⊂平面ABC,
1 1 1 1
所以AC ⊥C B.
1
又因为BC ∩BH = B,所以AC ⊥平面BBCC,因此
1 1 1
AC ⊥ BB . .............................................7分
1
(2)由(1)可知,CA,CB,BC 两两垂直,如图,以C为原点建立空间直角坐标系.
1
则A(2,0,0),B(0,2,0),C (0,2,2),B (0,4,2),B A = BA=(2,−2,0).
1 1 1 1
设BP=λB A =(2λ,−2λ,0),λ∈[0,1],
1 1 1
则P(2λ,4−2λ,2). .............................................9分
设平面PBC的一个法向量为n =(x,y,z),
1
因为BP=(2λ,2−2λ,2),CB=(0,2,0),
n ⋅BP=0, 2λx+(2−2λ)y+2z =0,
所以 1 即
n ⋅CB=0, 2y =0,
1
z =−λx,
则有
y =0.
令x=1,得n =(1,0,−λ).10分
1而平面BCC 的一个法向量可以是n =(1,0,0),
1 2
n ⋅n (1,0,−λ)⋅(1,0,0) 3 10 1
则 cos n ,n = 1 2 = = ,解得λ= ,
1 2 n ⋅ n 1+λ2 10 3
1 2
BP 1
即P为棱B A 的三等分点, 1 = . .............................................15分
1 1 AB 3
1 1
1
18.(17分)【解析】(1)依题意,设切点(x ,lnx −x +a),求导得 f′(x)= −1,
0 0 0 x
1 1
则 f′(x )= −1=e−1,解得x = ,又 f(x )=(e−1)x ,(e−1)x =lnx −x +a,则a=2,
0 x 0 e 0 0 0 0 0
0
所以实数a的值为2. ............................................. 6分
(2)依题意,g(x)=x(lnx−x+a)的定义域为(0,+∞),
1
求导得g′(x)=lnx−x+a+( −1)x=lnx−2x+a+1,
x
则g′(x)=0有两个不等的正根x,x ,且是g′(x)的变号零点,
1 2
1
令h(x)=lnx−2x+a+1,x>0,求导得h′(x)= −2,
x
1 1
当00,当x> 时,h′(x)<0,
2 2
1 1
于是函数h(x)在(0, )上单调递增,在( ,+∞)上单调递减,
2 2
1
由函数h(x)有两个零点,得h(x) =h( )=a−ln2>0,解得a>ln2, ...........................9分
max 2
1
此时h(e−3a)=−2a−2e−3a +1<1−2ln2<0,令ϕ(a)=lna−a+1,求导得ϕ′(a)= −1,
a
当ln20,
当a>1时,ϕ′(a)<0,函数ϕ(a)在(ln2,1)上递增,在(1,+∞)上递减,
则ϕ(a)≤ϕ(1)=0,即lna−a+1≤0,h(2a)=ln2a−3a+1=(lna−a+1)+(ln2−a)−a<0,
1
因此当a>ln2时,函数h(x)必有两个零点x,x ,且是变号零点,由x 1+ln( 1),只需证 >1+lnt,
2 1 x 2(t−1)
2
3lnt−tlnt 2(t−1)
即 >1,只证lnt− <0,
2(t−1) 3−t2(t−1)
令F(t)=lnt− ,00,
t (3−t)2 t(3−t)2 t(3−t)2
因此函数F(t)在(0,1)上单调递增,F(t)1+ln( 1). .............................................17分
2 1 x
2
|c−2| c+2
19.(17分)【解析】(1)方法(1)特殊值法,令M(±2,0), = ,且a=2c,解得c2 =2.
|a−2| a+2
x2 y2
∴a2 =8,b2 =a2 −c2 =6,椭圆C的方程为 + =1, ............................................. 5分
8 6
|MF | (x−c)2 + y2
方法(2)设M(x,y),由题意 = =λ(常数),整理得:
|MA| (x−a)2 + y2
2c−2aλ2
=0
2c−2aλ2 λ2a2 −c2 λ2 −1 c 1
x2 + y2 + x+ =0,故 ,又 = ,解得:a =2 2,c= 2.
λ2 −1 λ2 −1 λ2a2 −c2 a 2
=−4
λ2 −1
x2 y2
∴b2 =a2 −c2 =6,椭圆C的方程为 + =1. ............................................. 5分
8 6
1
|SB|⋅|SF |⋅sin∠BSF
S |SB| S |BF |
(2)(1) SBF = 2 = ,又 SBF = ,
S 1 |SD| S |DF |
SDF |SD|⋅|SF |⋅sin∠DSF SDF
2
|BS| |BF | |BF |
∴ = (或由角平分线定理得),令 =λ ,则BF =λFD,设D ( x ,y ) ,
|DS| |DF | |DF | 0 0
x = 2(λ+1)−λx
则有3x2 +4y2 =24,又直线l的斜率k >0,则x ∈(−2 2, 2), B 0
0 0 0 y =−λy
B 0
2
代人3x2 +4y2 −24=0得:3 2(1+λ)−λx +4λ2y2 −24=0,即
0 0
( )
(λ+1) 5λ−3− 2λx =0,
0
3 1
λ>0,∴λ= ∈ ,1. ............................... 11分
5− 2x 3
0
|SB| |TB| |BF |
(2)由(1)知, = = ,由阿波罗尼斯圆定义知,
|SD| |TD| |DF |
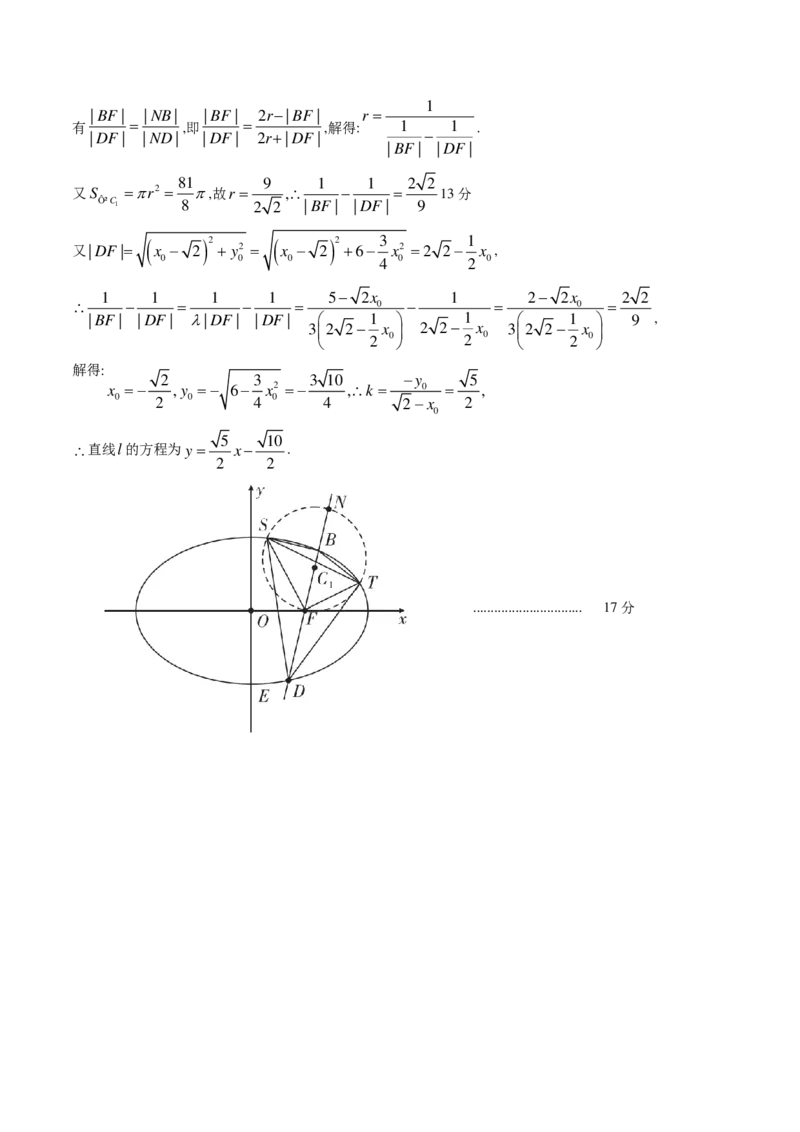
S,T,F在以B,D为定点的阿波罗尼斯圆上,设该圆圆心为C ,半径为r,与直线l的另一个交点为N ,则
11
|BF | |NB| |BF | 2r−|BF | r =
有 = ,即 = ,解得: 1 1 .
|DF | |ND| |DF | 2r+|DF | −
|BF | |DF |
81 9 1 1 2 2
又S =πr2 = π,故r = ,∴ − = 13分
Ô² C 1 8 2 2 |BF | |DF | 9
( )2 ( )2 3 1
又|DF |= x − 2 + y2 = x − 2 +6− x2 =2 2− x ,
0 0 0 4 0 2 0
1 1 1 1 5− 2x 1 2− 2x 2 2
∴ − = − = 0 − = 0 =
|BF | |DF | λ|DF | |DF | 1 1 1 9 ,
32 2− x 2 2− x 32 2− x
2 0 2 0 2 0
解得:
2 3 3 10 −y 5
x =− ,y =− 6− x2 =− ,∴k = 0 = ,
0 2 0 4 0 4 2−x 2
0
5 10
∴直线l的方程为y = x− .
2 2
............................... 17分