文档内容
2024 届高三下学期开学摸底考
参考答案
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个
选项是符合题目要求的.
1 2 3 4 5 6 7 8
C B B D D D C C
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题
目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
9.BC 10.BD 11.ACD 12.AC
三、填空题:本题共4小题,每小题5分,共20分.
13. 14. 2 15.829 16.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)
【详解】(1)因为 ,所以 即 .
在 中,由正弦定理得 .
在 中,由余弦定理得 ,
所以 ②.
因为 ,所以 ①.
将①代入②得 ,所以 ..........................5分
(2)结合(1)问:在 中,由余弦定理得 ,
.
因为 ,所以 .
因为 ,所以 .在 中,由正弦定理得 ,解得: ,
所以 ,
的面积 .
..........................10分
18.(12分)
【详解】(1)函数 的定义域为 .
将 代入 ,解得 ,即 ,
由切线方程 ,则切线斜率 .
故 ,解得 ..........................6分
(2)证明:由(1)知 ,
从而 等价于 .
设函数 ,则 .
所以当 时, ,当 时, .
故 在 上单调递减,在 上单调递增,
从而 在 上的最小值为 .
设函数 ,
从而 在 上的最大值为 .故 ,即 . .........................12分
19.(12分)
【详解】(1)一方面:因为 为正三角形且 为 的中点,所以 (三线合一),
又因为平面 平面 且平面 平面 ,并注意到 平面 ,
所以由面面垂直的性质可知 平面 ,
又因为 平面 ,
所以由线面垂直的性质可知 ;
另一方面:由题意不妨设 ,则 ,
因为 为正三角形且 为 的中点,所以 , ,
所以 ,且 ,注意到 与 均为
锐角,
所以 ,不妨设 ,
因为 ,
所以 ,即 .
综合以上两方面有 且 ,
注意到 , 平面 , 平面 ,
所有由线面垂直的判定有 平面 ,
又因为 平面 ,所以平面 平面 .. .........................6分
(2)由(1)可知 平面 ,则点 到平面 的距离即为 的长度,
一方面梯形 的面积为 , ,
所以有四棱锥 的体积为 ,
另一方面由题可知四棱锥 的体积为 ,结合以上两方面有 ,解得 ,
因为 ,所以 ,由(1)可知 ,
所以 ,所以 ,
所以 . . .........................12分
20.(12分)
【详解】(1) 三人均被分至同一队,即三人同分至甲队或乙队,
记事件 “ 被分至甲队”, 事件 “ 被分至甲队”, 事件 “ 被分至甲队”,
当 即将摸球时,箱中有2个红球和2个黑球,则 被分至甲队即 摸出红球的概率为 ;
当 被分至甲队时,箱中有2个红球和3个黑球,则 被分至甲队即 摸出红球的概率为
;
当 均被分至甲队时,箱中有2个红球和4个黑球,则 被分至甲队即 摸出红球的概率为
;
所以 ,则 ,
同理知:新增登山爱好者 均被分至乙队的概率也为 ,
所以 三人均被分至同一队的概率为 .. . .........................6分
(2)由题设, 可能取值为 ,
为新增的4名登山爱好者被分至同一队,则 ,
为新增的4名登山爱好者中有3名均被分至同一队,其余1名被分至另一队,
设新增的第 名登山爱好者被单独分至甲队或乙队,则
, ,
, ,
所以 ,
为新增的4名登山爱好者中各有2名被分至甲队和乙队,则,
所以 .. . .........................12分
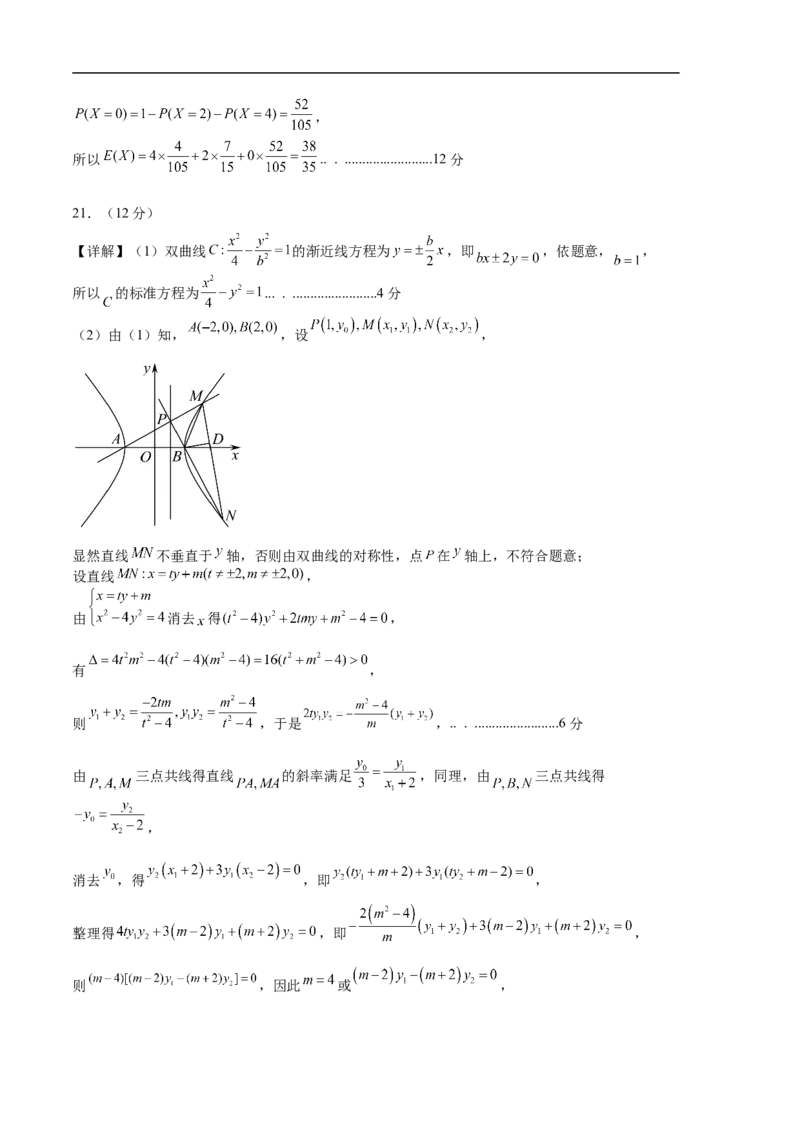
21.(12分)
【详解】(1)双曲线 的渐近线方程为 ,即 ,依题意, ,
所以 的标准方程为 ... . ........................4分
(2)由(1)知, ,设 ,
显然直线 不垂直于 轴,否则由双曲线的对称性,点 在 轴上,不符合题意;
设直线 ,
由 消去 得 ,
有 ,
则 ,于是 ,.. . ........................6分
由 三点共线得直线 的斜率满足 ,同理,由 三点共线得
,
消去 ,得 ,即 ,
整理得 ,即 ,
则 ,因此 或 ,若 ,又 ,得 ,
结合 ,从而 ,即 ,不成立,
即 ,因此 ,满足 ,.. . .........................10分
则直线 恒过点 ,点 在以 为直径的圆 上,
当 与 重合时, 最大,此时 轴, ,
所以当 最大时,点 的纵坐标为 ... . .........................12分
22.(12分)
【详解】(1)由 , ,
若 ,则 ,即 ,此时 ,
当 ,则 ,即 ;
当 ,则 ,即 ;
若 ,则 ,即 ,此时 ,
当 ,则 ,即 ;
当 ,则 ,即 (舍);
综上, 的所有可能值为 .... . .........................3分
(2)由(1)知: ,则 ,
数列 中的项存在最大值,故存在 使 , ,
由 ,
所以 ,故存在 使 ,
所以0为数列 中的项;... . ........................7分(3)不存在,理由如下:由 ,则 ,
设 ,
若 ,则 , ,
对任意 ,取 ( 表示不超过 的最大整数),
当 时,
;
若 ,则 为有限集,
设 , ,
对任意 ,取 ( 表示不超过 的最大整数),
当 时,
;
综上,不存在正实数M,使得对任意的正整数n,都有 .... . .........................12分