南充高中高2023级第四学期第一次月考数学_2024-2025高二（7-7月题库）_2025年04月试卷(1)_0406四川省南充市高级中学2024-2025学年高二下学期4月考试题

南充高中高 2023 级第四学期第一次月考
数学试卷
（考试时间：120分钟 满分：150分 命审题：童俊璋 杨秦飞 ）
注意事项：
1．答题前，务必将自己的姓名、班级、考号填写在答题卡规定的位置上。
2．答选择题时，必须使用2B铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦
干净后，再选涂其它答案标号。
3．答非选择题时，将答案书写在答题卡相应位置上，写在本试卷上无效。
第I卷（选择题）
一、单选题：本题共8题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目
要求的.
1．在等比数列a 中， 是方程 的两根，则 （ ）
n
2
A．  3,  9 B  ．−8  +2 = 0 C．  6 = D．
2. 已知圆 2 关 − 于 2 直线 ± 对称 2 ，则实数 （ ） 3± 5
2 2
A．6  :  +  +2  −4  +1 =B． 0 4   +2  −1=C． 03  = D．7
3. 下列求导运算正确的是（ ）
A． B．
'  ' 1
4 =−    4   (2  −1) = 2  −1
C． D．
'  ' 1
4.已知等 2 差数 = 列 2 a 的前n项和为S ， ， ，则 （ 1+ ）    = 
n n
3 =16  6 =8  12 =
A． B． C． D．
20 8
5.已知抛 − 物 3 线 的焦点 − 为 8 F 0 2,0，过点F 的直线l − 与 24 抛物线C的一个交点为 3 Am,8，
2
则直线l的方程  :为  （=2）    >0
A． B．
C．
4  +3  −8= 0
D．
3  +4  −6= 0
6.设函数4  f−x3  在−8= 0处存在导数为2，则 （3  −）4  −6= 0
0+   −   0−  
=  0      →0   =2
A．1 B．2 C． D．4
3
7.记 ￡表示点 到曲线￡上任意一点距离的最小值.已知圆 ： ，圆 ：
2 2
, ，若点  为圆 上的一点，则 的最大值为  （ 1 ）  +  −3 =1  2  −
2 2
4 A+ ．  =4   1 B．  (  ,  2) C． D．
试卷第1页，共4页
4 5 8 3x2 y2
8．已知双曲线C:  1的两焦点分别为F 、F ，过右焦点F 作直线 交右支于 、点，且 ，
a2 b2 1 2 2
   =3    2
若∠ ，则双曲线 的离心率为（ ）

1  7  = 3  3 5 7
A． B． C． D．
5 2 3 3
二、多选题：本题共3小题，每小题6分，共18分，在每小题给出的选项中，有多项符合题目要求.
全部选对的得6分，部分选对的得部分分，有选错的得0分.
9.已知数列 是公差小于0的等差数列，前n项和为S ，满足 ，下列选项正确的有（ ）
n
A．   B． C  ．1+5  最3小 =  8 D．
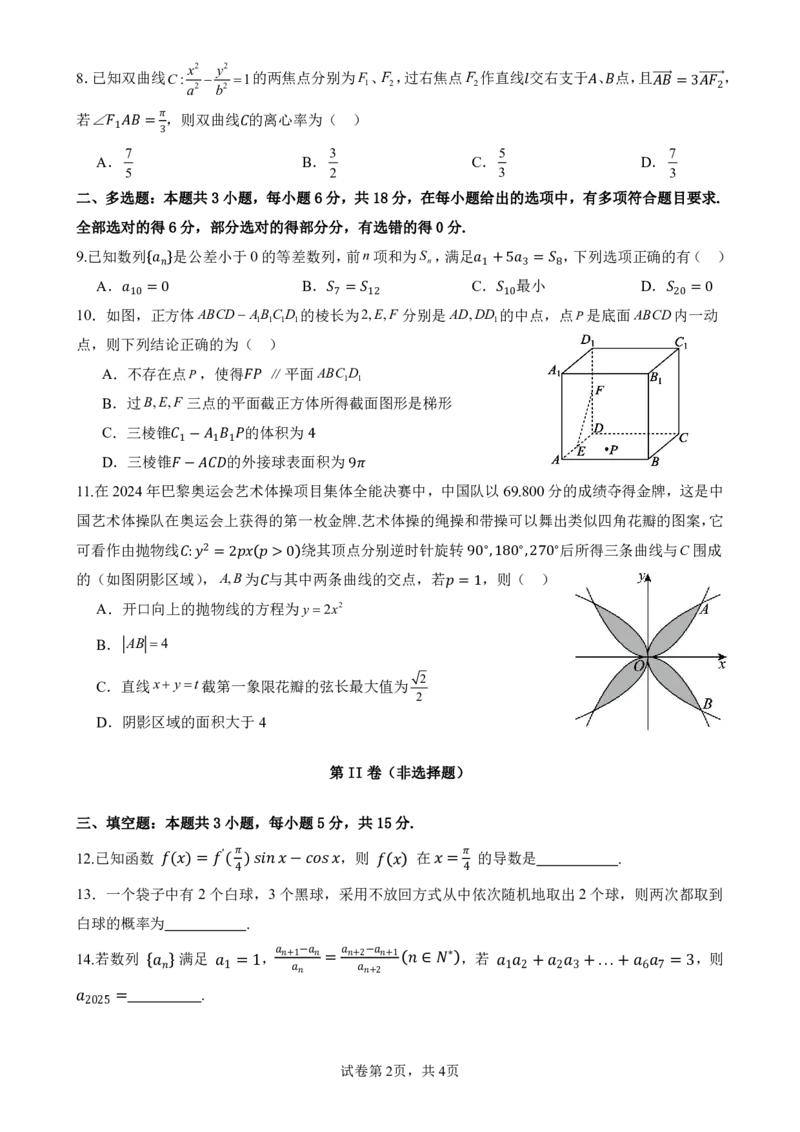
10．如图  1，0 = 正 0 方体ABCD A 1 B 1 C 1 D 1 的棱  长7 为 =  21,2E,F 分别是AD,DD 1  的10中点，点P是底面ABCD  内20一 = 动 0
点，则下列结论正确的为（ ）
A．不存在点P，使得 ∥平面ABC D
1 1
B．过B,E,F 三点的平

面

截正方体所得截面图形是梯形
C．三棱锥 的体积为
D．三棱锥  1−  1  的1  外接球表面 4 积为
11.在2024年巴

黎
−
奥

运

会艺术体操项目集体
9
全

能决赛中，中国队以69.800分的成绩夺得金牌，这是中
国艺术体操队在奥运会上获得的第一枚金牌.艺术体操的绳操和带操可以舞出类似四角花瓣的图案，它
可看作由抛物线 绕其顶点分别逆时针旋转 后所得三条曲线与C围成
2 ∘ ∘ ∘
的（如图阴影区域  : ）  ， = A, 2 B  为   与 > 其 0 中两条曲线的交点，若 90 ， ,1 则 80 （ ,27 ） 0
A．开口向上的抛物线的方

程为y2x2
=1
B． AB 4
C．直线xyt截第一象限花瓣的弦长最大值为 2
2
D．阴影区域的面积大于4
第II卷（非选择题）
三、填空题：本题共3小题，每小题5分，共15分.
12.已知函数 ，则 在 的导数是 .
'  
13．一个袋子  中(  有) =2个  白(4球)  ，   3  个−黑  球   ，  采用不  放  回方式  从=中4依次随机地取出2个球，则两次都取到
白球的概率为 .
14.若数列 满足 ， ，若 ，则
+1−     +2−   +1 ∗
.  1 = 1   =   +2  ∈   1  2 +  2  3 +...+  6  7 = 3
2025 =
试卷第2页，共4页四、解答题：本题共5小题，共77分.解答写出必要的文字说明，证明过程或演算步骤.
15.（本小题共13分）
某高校的入学面试中有3道难度相当的题目，李明答对每道题目的概率都是0.6．若每位面试者共有
三次机会，一旦某次答对抽到的题目，则面试通过，否则就一直抽题到第3次答完为止．
(1)求李明第二次答题通过面试的概率；
(2)求李明最终通过面试的概率．
16. （本小题共15分）
已知函数 .
2
(1)若  ，  求=  −；2  
'
(2)若
=1
在

处的切线与直线 垂直，求a.
1,  1   −3  −2= 0
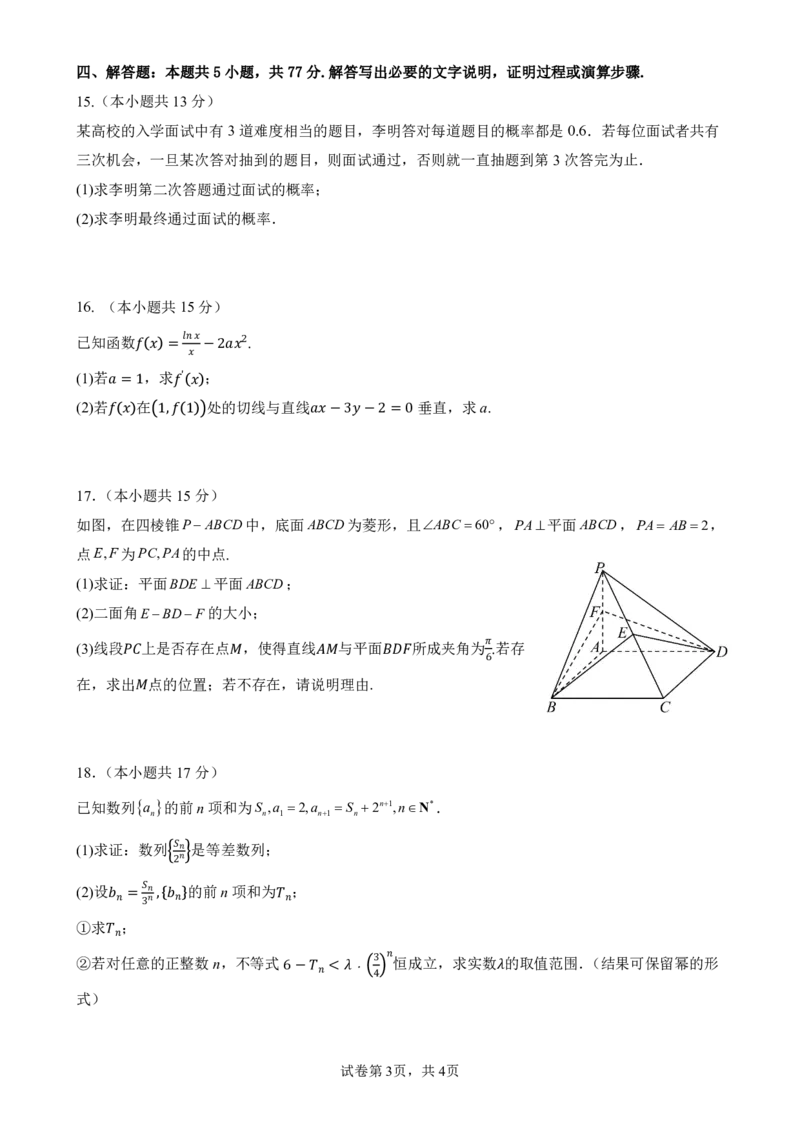
17．（本小题共15分）
如图，在四棱锥PABCD中，底面ABCD为菱形，且ABC 60，PA平面ABCD，PA AB2，
点E,F为PC,PA的中点.
(1)求证：平面BDE 平面ABCD；
(2)二面角EBDF 的大小；
(3)线段 上是否存在点 ，使得直线 与平面 所成夹角为 .若存

在，求出   点的位置；若  不存在，请说  明  理由.    6

18．（本小题共17分）
已知数列a 的前n项和为S ,a 2,a S 2n1,nN*．
n n 1 n1 n
(1)求证：数列 是等差数列；


2
(2)设 的前n项和为 ；

①求   ；=3  ,    
②若对   任意的正整数n，不等式 ﹒ 恒成立，求实数 的取值范围．（结果可保留幂的形

3
式） 6−   <  4 
试卷第3页，共4页19．（本小题共17分）
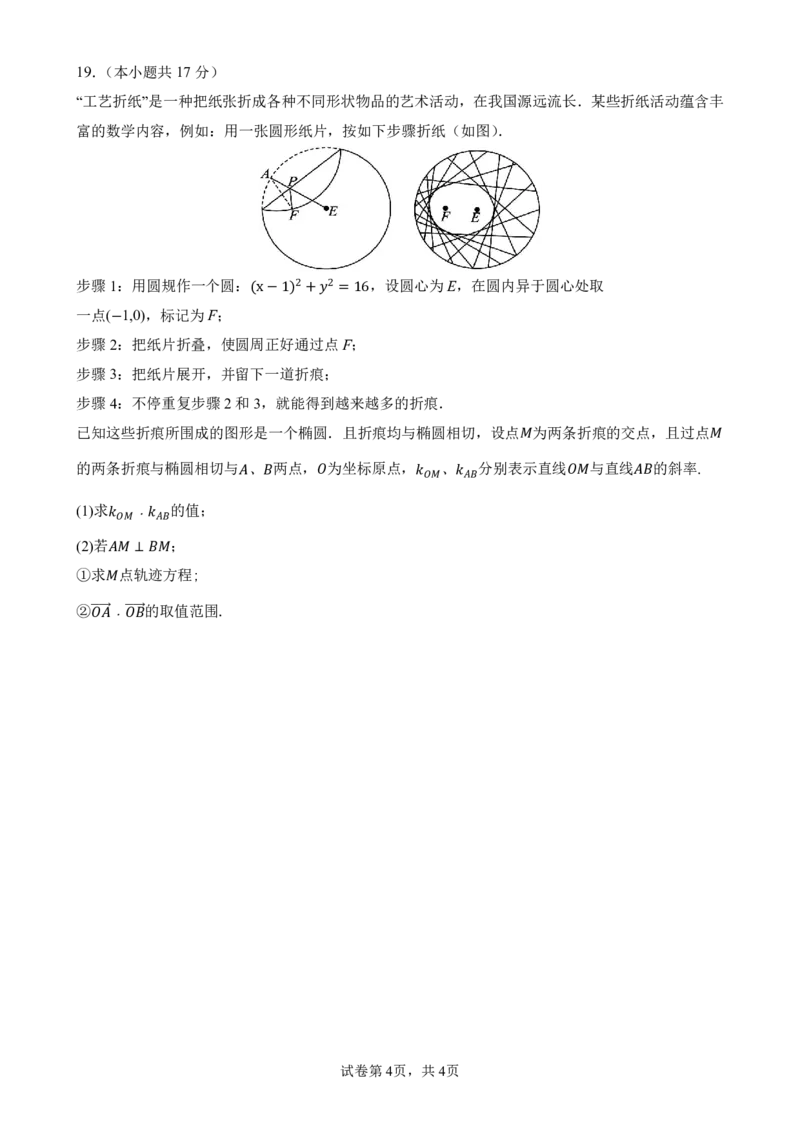
“工艺折纸”是一种把纸张折成各种不同形状物品的艺术活动，在我国源远流长．某些折纸活动蕴含丰
富的数学内容，例如：用一张圆形纸片，按如下步骤折纸（如图）．
步骤1：用圆规作一个圆： ，设圆心为E，在圆内异于圆心处取
2 2
一点( 1,0)，标记为F；
(x−1) +  =16
步骤2− ：把纸片折叠，使圆周正好通过点F；
步骤3：把纸片展开，并留下一道折痕；
步骤4：不停重复步骤2和3，就能得到越来越多的折痕．
已知这些折痕所围成的图形是一个椭圆．且折痕均与椭圆相切，设点 为两条折痕的交点，且过点
的两条折痕与椭圆相切与 、 两点， 为坐标原点， 、 分别表  示直线 与直线 的斜率. 

(1)求 ﹒ 的值；
(2)若       ；
①求 点轨迹方程;
⊥  
②  ﹒ 的取值范围.
      
试卷第4页，共4页