文档内容
级⾼⼆ ⽉⽉考
2024 12
数学试题
本试卷满分150分,考试时间120分钟.
注意事项:
1.答题前,务必将⾃⼰的班级、姓名、考号填写在答题卡规定的位置上.
2.答选择题时,必须使⽤2B铅笔将答题卡上对应题⽬的答案标号涂⿊,如需改动,⽤橡⽪
擦⼲净后,再选涂其它答案标号.
3.答⾮选择题时,必须使⽤0.5毫⽶⿊⾊签字笔,将答案写在答题卡规定的位置上.
4.所有题⽬必须在答题卡上作答,在试题卷上答题⽆效.
5.考试结束后,只将答题卡交回.⼀、选择题:本题共8⼩题,每⼩题5分,共40分.在
每⼩题给出的四个选项中,只有⼀个选项是符合题⽬要求的.
1. 某种细菌在⽣⻓过程中,每10分钟分裂⼀次(由⼀个分裂为两个),经过50分钟后,此细菌可由⼀个分
裂成( )
A. 个 B. 个 C. 个 D. 个
2. 已知随机变量X服从正态分布 ,则 ( )
(参考数据: , )
A.0.3413 B.0.4772 C.0.6826 D.0.9544
3. 已知数列 满⾜对任意的 ,都有 .若 ,则 ( )
A.1 B.2
C.3 D.4
4. 曲线 在点 处的切线斜率为( )
A.2 B.1 C. D.
5. 已知随机变量 服从⼆项分布 ,且 ,则 ( )
A.10 B.16 C.18 D.20
6. 抛掷甲、⼄两枚质地均匀的骰⼦,在已知甲骰⼦的点数为偶数的条件下,⼄骰⼦的点数⼩于甲骰⼦的点
第1⻚/共5⻚
学科⽹(北京)股份有限公司数的概率为( )
A. B. C. D.
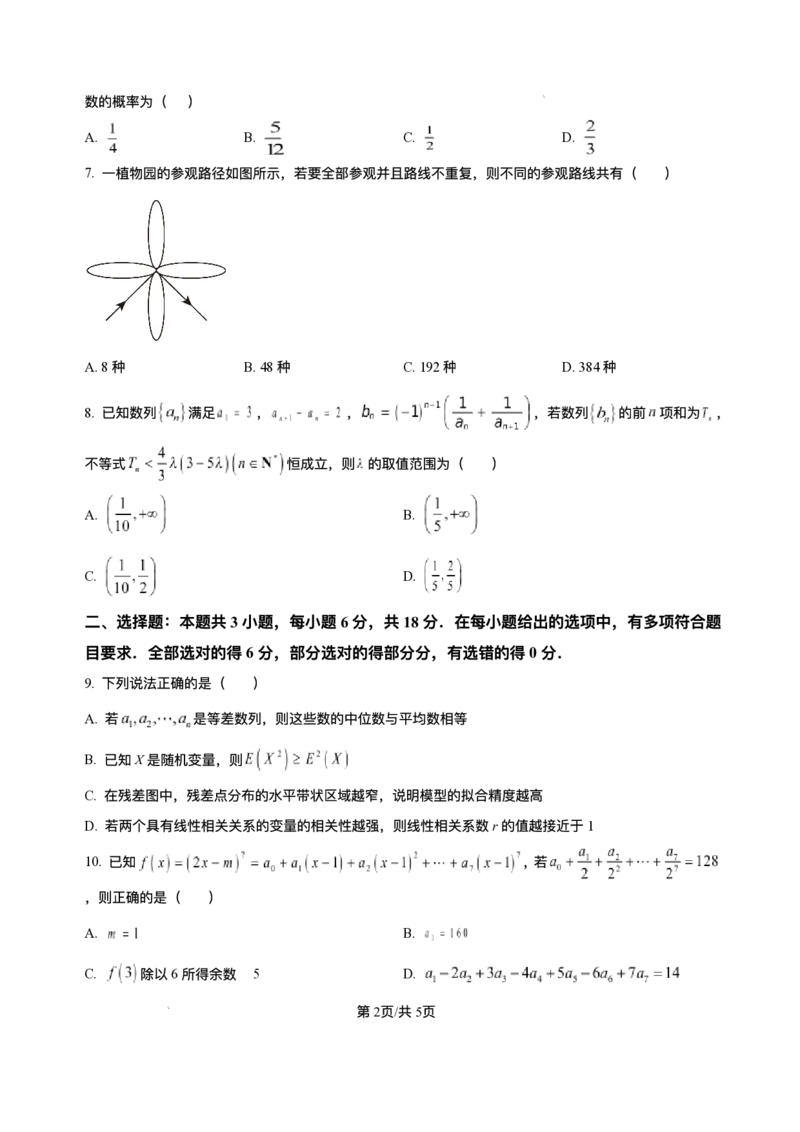
7. ⼀植物园的参观路径如图所示,若要全部参观并且路线不重复,则不同的参观路线共有( )
A.8种 B.48种 C.192种 D.384种
8. 已知数列 满⾜ , , ,若数列 的前 项和为 ,
不等式 恒成⽴,则 的取值范围为( )
A. B.
C. D.
⼆、选择题:本题共3⼩题,每⼩题6分,共18分.在每⼩题给出的选项中,有多项符合题
⽬要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 下列说法正确的是( )
A. 若 是等差数列,则这些数的中位数与平均数相等
B. 已知X是随机变量,则
C. 在残差图中,残差点分布的⽔平带状区域越窄,说明模型的拟合精度越⾼
D. 若两个具有线性相关关系的变量的相关性越强,则线性相关系数r的值越接近于1
10. 已知 ,若
,则正确的是( )
A. B.
C. 除以6所得余数 5 D.
第2⻚/共5⻚
学科⽹(北京)股份有限公司11. 已知 ,下列说法正确的是( )
A. 在 处的切线⽅程为 B. 的单调递减区间为
C. 的极⼤值为 D. ⽅程 有两个不同的解
三、填空题:本题共3⼩题,每⼩题5分,共15分.
12. 已知 为等差数列, ,则 ________.
13. 已知某地市场上供应的⼀种电⼦产品中,甲⼚产品占80%,⼄⼚产品占20%,甲⼚产品的合格率是70%,
⼄⼚产品的合格率是80%,则从该地市场上买到⼀个合格产品的概率是______.
14. 若不等式 ( 是⾃然对数的底数)对任意 恒成⽴,则当 取最⼤值时,实
数 __________.
四、解答题:本题共5⼩题,共77分.解答应写出⽂字说明、证明过程或演算步骤.
15. 已知等差数列 的公差不为零, ,且 , , 成等⽐数列.
(1)求数列 的通项公式;
(2)设数列 的前 项和为 ,数列 的前 项和为 ,若 ,求 的最⼤值.
16. 某种机械设备随着使⽤年限的增加,它的使⽤功能逐渐减退,使⽤价值逐年减少,通常把它使⽤价值逐
年减少的“量”换算成费⽤,称之为“失效费”.某种机械设备的使⽤年限 (单位:年)与失效费 (单位:
万元)的统计数据如下表所示:
使⽤年限 (单位:年) 2 4 5 6 8
失效费 (单位:万元) 3 4 5 6 7
(1)根据上表数据,计算 与 的相关系数 ,并说明 与 的线性相关性的强弱.
(已知: ,则认为 与 线性相关性很强; ,则认为与 线性相关性⼀般;
,则认为 与 线性相关性较弱)( 的结果精确到0.0001)
(2)求 关于 的线性回归⽅程,并估算该种机械设备使⽤10年的失效费.
第3⻚/共5⻚
学科⽹(北京)股份有限公司附:样本 的相关系数 ,经验回归⽅程 的
斜率和截距的最⼩⼆乘估计分别为 , .
17. 据世界⽥联官⽅⽹站消息,原定于2023年5⽉ ⽇在中国⼴州举办 世界⽥联接⼒赛延期⾄2025
年4⽉⾄5⽉举⾏.据了解,甲、⼄、丙三⽀队伍将会参加2025年4⽉⾄5⽉在⼴州举⾏的 ⽶接⼒的
⻆逐.接⼒赛分为预赛、半决赛和决赛,只有预赛、半决赛都获胜才能进⼊决赛.已知甲队在预赛和半决赛中获
胜的概率分别为 和 ;⼄队在预赛和半决赛中获胜的概率分别为 和 ;丙队在预赛和半决赛中获胜的
概率分别为 和 .
(1)甲、⼄、丙三队中,谁进⼊决赛的可能性最⼤;
(2)设甲、⼄、丙三队中进⼊决赛的队伍数为 ,求 的分布列.
18. 已知 (e为⾃然对数的底数)
(1)求曲线 在点 处 切线⽅程;
(2)求证:当 时, 恒成⽴;
(3)已知 ,如果当 时, 恒成⽴,求 的最⼤值.
19. ⻢尔可夫链是因俄国数学家安德烈·⻢尔可夫得名,其过程具备“⽆记忆” 性质,即第 次状态的概
率分布只跟第 次的状态有关,为了避免就餐聚集和减少排队时间,某校开学后,⻝堂从开学第⼀天起,每
餐只推出即点即取的⽶饭套餐和⾯⻝套餐.已知某同学每天中午会在⻝堂提供的两种套餐中选择,已知他
第⼀天选择⽶饭套餐的概率为 ,⽽前⼀天选择了⽶饭套餐后⼀天继续选择⽶饭套餐的概率为 ,前⼀天
选择⾯⻝套餐后继续选择⾯⻝套餐的概率为 ,如此往复.
(1)求该同学第⼆天中午选择⽶饭套餐 概率;
(2)记该同学第 天选择⽶饭套餐的概率为 ;
第4⻚/共5⻚
学科⽹(北京)股份有限公司①证明: 为等⽐数列;
②当 时, 恒成⽴,求 取值范围.
第5⻚/共5⻚
学科⽹(北京)股份有限公司级⾼⼆ ⽉⽉考
2024 12
数学试题
本试卷满分150分,考试时间120分钟.
注意事项:
1.答题前,务必将⾃⼰的班级、姓名、考号填写在答题卡规定的位置上.
2.答选择题时,必须使⽤2B铅笔将答题卡上对应题⽬的答案标号涂⿊,如需改动,⽤橡⽪
擦⼲净后,再选涂其它答案标号.
3.答⾮选择题时,必须使⽤0.5毫⽶⿊⾊签字笔,将答案写在答题卡规定的位置上.
4.所有题⽬必须在答题卡上作答,在试题卷上答题⽆效.
5.考试结束后,只将答题卡交回.⼀、选择题:本题共8⼩题,每⼩题5分,共40分.在
每⼩题给出的四个选项中,只有⼀个选项是符合题⽬要求的.
1. 某种细菌在⽣⻓过程中,每10分钟分裂⼀次(由⼀个分裂为两个),经过50分钟后,此细菌可由⼀个分
裂成( )
A 个 B. 个 C. 个 D. 个
【答案】D
【解析】
【分析】由题意可得 分钟后共有 个,将 代⼊求解即可.
【详解】由题意可得⼀个细菌10分钟后共有 个,20分钟后共有 个,……,
从⽽得到 分钟后共有 个,
所以经过5次分裂(即50分钟后),有 个.
故选;D.
2. 已知随机变量X服从正态分布 ,则 ( )
(参考数据: , )
A.0.3413 B.0.4772 C.0.6826 D.0.9544
【答案】B
【解析】
【分析】根据正态分布的性质写出 ,再根据正态分布知识即可求解.
第1⻚/共17⻚
学科⽹(北京)股份有限公司【详解】 随机变量X服从正态分布 ,
,
,
根据正态分布对称性可得
故选:B.
3. 已知数列 满⾜对任意 ,都有 .若 ,则 ( )
A.1 B.2
C.3 D.4
【答案】D
【解析】
【分析】根据已知条件赋值可求得结果.
【详解】因为 ,
所以 .
故选:D.
4. 曲线 在点 处的切线斜率为( )
A.2 B.1 C. D.
【答案】A
【解析】
【分析】利⽤商的导数来求切线斜率即可.
【详解】求导得: ,
当 时,切线斜率 ,
故选:A.
5. 已知随机变量 服从⼆项分布 ,且 ,则 ( )
第2⻚/共17⻚
学科⽹(北京)股份有限公司A.10 B.16 C.18 D.20
【答案】D
【解析】
【分析】应⽤⼆项分布的⽅差 ,计算求得 ,结合⼆项分布的期望计算可得结果.
【详解】因为 ,解得 ,
所以 ,则 .
故选:D
6. 抛掷甲、⼄两枚质地均匀的骰⼦,在已知甲骰⼦的点数为偶数的条件下,⼄骰⼦的点数⼩于甲骰⼦的点
数的概率为( )
A. B. C. D.
【答案】C
【解析】
【分析】⾸先确定甲骰⼦的点数为偶数的可能情况和概率,然后求甲骰⼦的点数为偶数的每种情况下⼄骰
⼦的点数⼩于甲骰⼦的点数可能情况和概率,最后相加即是最后结果.
【详解】设事件A为“甲骰⼦的点数为偶数”,那么点数的可能性为2,4,6,
⽽且每种可能性的概率为 .
当甲骰⼦的点数为2时,要使得⼄骰⼦的点数⼩于甲骰⼦的点数,此时⼄骰⼦的点数只能是1,
此种情况概率为 .
当甲骰⼦的点数为4时,要使得⼄骰⼦的点数⼩于甲骰⼦的点数,此时⼄骰⼦的点数是1,2,3,
此种情况概率为 .
当甲骰⼦的点数为6时,要使得⼄骰⼦的点数⼩于甲骰⼦的点数,此时⼄骰⼦的点数是1,2,3,4,5,
此种情况概率为 .
所以甲骰⼦的点数为偶数的条件下,⼄骰⼦的点数⼩于甲骰⼦的点数的概率为:
.
第3⻚/共17⻚
学科⽹(北京)股份有限公司故在已知骰⼦甲骰⼦的点数为偶数的条件下,⼄骰⼦的点数⼩于甲骰⼦的点数的概率为
故选:C.
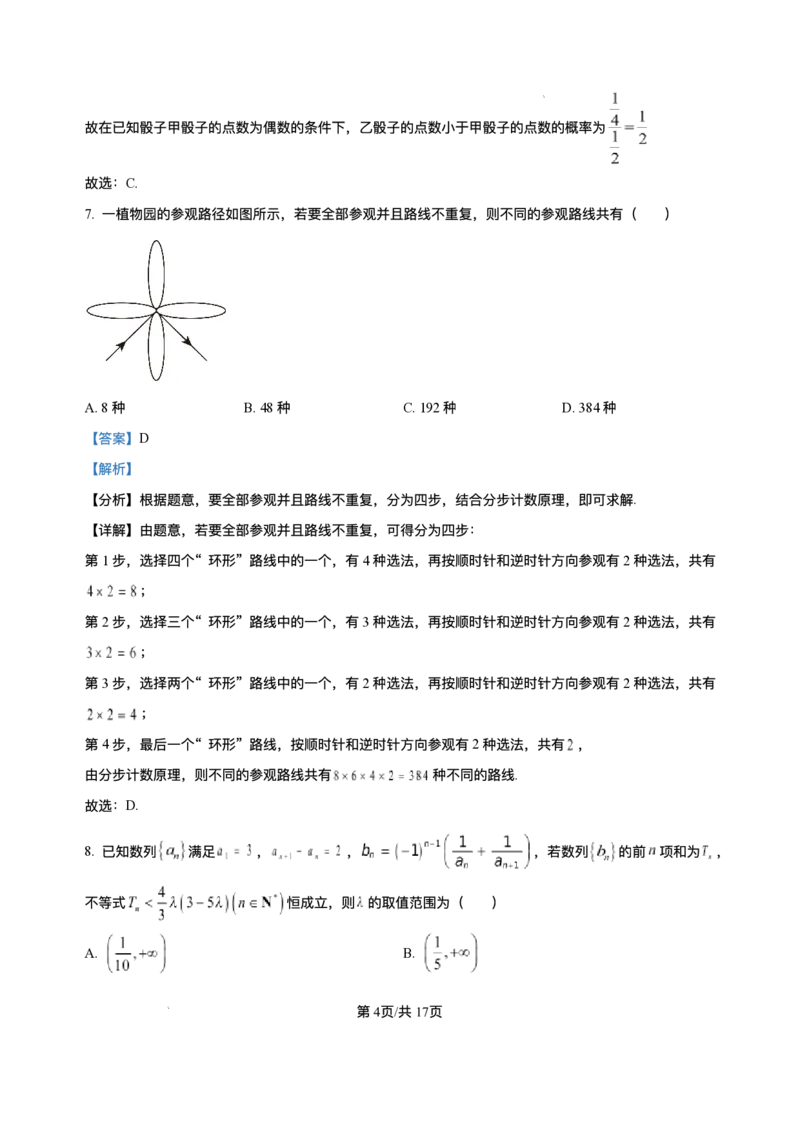
7. ⼀植物园的参观路径如图所示,若要全部参观并且路线不重复,则不同的参观路线共有( )
A.8种 B.48种 C.192种 D.384种
【答案】D
【解析】
【分析】根据题意,要全部参观并且路线不重复,分为四步,结合分步计数原理,即可求解.
【详解】由题意,若要全部参观并且路线不重复,可得分为四步:
第1步,选择四个“ 环形” 路线中的⼀个,有4种选法,再按顺时针和逆时针⽅向参观有2种选法,共有
;
第2步,选择三个“ 环形” 路线中的⼀个,有3种选法,再按顺时针和逆时针⽅向参观有2种选法,共有
;
第3步,选择两个“ 环形” 路线中的⼀个,有2种选法,再按顺时针和逆时针⽅向参观有2种选法,共有
;
第4步,最后⼀个“ 环形” 路线,按顺时针和逆时针⽅向参观有2种选法,共有 ,
由分步计数原理,则不同的参观路线共有 种不同的路线.
故选:D.
8. 已知数列 满⾜ , , ,若数列 的前 项和为 ,
不等式 恒成⽴,则 的取值范围为( )
A. B.
第4⻚/共17⻚
学科⽹(北京)股份有限公司C. D.
【答案】D
【解析】
【分析】先求得数列 的通项公式,进⽽可得 ,进⽽分 为偶数与奇数两种情况求
得 ,进⽽可得 ,求解即可.
【详解】因为数列 满⾜ , ,
所以数列 是以 为⾸项,2为公差的等差数列,
所以 ,
所以 ,记 ,
则 ,即
当 为偶数时, ,
当 为奇数时, ,
因为不等式 恒成⽴,即 ,
所以 ,
所以 , ,
所以解得 ,所以 的取值范围为 .
故选:D.
⼆、选择题:本题共3⼩题,每⼩题6分,共18分.在每⼩题给出的选项中,有多项符合题
⽬要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 下列说法正确的是( )
A. 若 是等差数列,则这些数的中位数与平均数相等
B. 已知X是随机变量,则
第5⻚/共17⻚
学科⽹(北京)股份有限公司C. 在残差图中,残差点分布的⽔平带状区域越窄,说明模型的拟合精度越⾼
D. 若两个具有线性相关关系的变量的相关性越强,则线性相关系数r的值越接近于1
【答案】ABC
【解析】
【分析】根据等差数列的性质可判断A,根据⽅差的性质可判断B,根据残差图的性质可判断C,根据相关
系数的性质可判断D.
【详解】对于A,对于等差数列,⽆论项数n为奇数或偶数,中位数均为⾸项与末项的平均数,
根据等差数列的性质可知,⾸项与末项的平均数即为整体的平均数,
所以等差数列的中位数和平均数相等,故A正确;
对于B,由⽅差的性质可知, ,
所以 ,故B正确;
对于C,在残差图中,残差点分布的⽔平带状区域越窄,说明模型的拟合精度越⾼,故C正确;
对于D,若两个具有线性相关关系的变量的相关性越强,则线性相关系数r的绝对值越接近于1,故D错误.
故选:ABC.
10. 已知 ,若
,则正确的是( )
A. B.
C. 除以6所得余数为5 D.
【答案】ACD
【解析】
【分析】令 ,已知式变为 ,可求得 判断A;
令 ,⼆项式化为 ,可求得 判断B;
,利⽤⼆项式展开式可判断除以6所得余数,判断C;
⼆项式两边都对 求导后令 可求得 ,从⽽判断D.
【详解】令 ,得 ∴ ,所以A正确;
第6⻚/共17⻚
学科⽹(北京)股份有限公司令 ∴ ,所以 ,所以B错误;
由A知 ,
所以 ,
所以 除以6的余数为5,C正确;
对于D,由 ,
两边求导可得 ,
令 ,得 ,所以D正确.
故选:ACD
11. 已知 ,下列说法正确的是( )
A. 在 处的切线⽅程为 B. 的单调递减区间为
C. 的极⼤值为 D. ⽅程 有两个不同的解
【答案】BC
【解析】
【分析】对于A,利⽤导数的⼏何意义求解,对于B,求导后,由导数⼩于零求解,对于C,求导后求极值,
对于D,函数 与 的交点个数判断
【详解】对于A,由 ( ),得 , ,则 ,所以 在
处的切线⽅程为 ,所以A错误,
对于B,由 ,得 , ,所以 的单调递减区间为 ,所以B正确,
对于C,由 ,得 ,当 时, ,当 时, ,所以当 时,
取得极⼤值 ,所以C正确,
对于D,由C选项可知 的最⼤值为 ,且当 时, ,当 时,
, 所以函数 与 的交点个数为1,所以 有1个解,所以D错误,
故选:BC
第7⻚/共17⻚
学科⽹(北京)股份有限公司三、填空题:本题共3⼩题,每⼩题5分,共15分.
12. 已知 为等差数列, ,则 ________.
【答案】2
【解析】
【分析】直接利⽤等差数列的下标性质求解即可.
【详解】因为 是等差数列且 ,
所以,由等差数列的性质可得 ,故答案为2.
【点睛】本题主要考查等差数列的性质,属容易题.等差数列的性质:若 ,则
.
13. 已知某地市场上供应的⼀种电⼦产品中,甲⼚产品占80%,⼄⼚产品占20%,甲⼚产品的合格率是70%,
⼄⼚产品的合格率是80%,则从该地市场上买到⼀个合格产品的概率是______.
【答案】0.72##
【解析】
【分析】利⽤全概率公式求解从该地市场上买到⼀个合格产品的概率,需要先确定不同⼚家产品的概率以
及在各⼚家产品条件下买到合格产品的概率,再根据全概率公式计算最终结果.
【详解】设“买到的产品是甲⼚产品”为事件 ,“买到的产品是⼄⼚产品”为事件 .
已知甲⼚产品占 ,⼄⼚产品占 ,所以 , .
记“从该地市场上买到⼀个合格产品”为事件 .
因为甲⼚产品 合格率是 ,所以在买到甲⼚产品的条件下,产品合格的概率 ;
⼜因为⼄⼚产品的合格率是 ,所以在买到⼄⼚产品的条件下,产品合格的概率 .
根据全概率公式 .
将 , , , 代⼊上式可得:
故答案为: .
14. 若不等式 ( 是⾃然对数的底数)对任意 恒成⽴,则当 取最⼤值时,实
数 __________.
第8⻚/共17⻚
学科⽹(北京)股份有限公司【答案】
【解析】
【分析】根据题意,令 ,可知当 时符合题意,利⽤导数可得函数 的单
调性和最⼩值 ,其中 ,令最⼩值⼤于或等于0,
进⽽得解.
【详解】由题意可知 ,令 ,
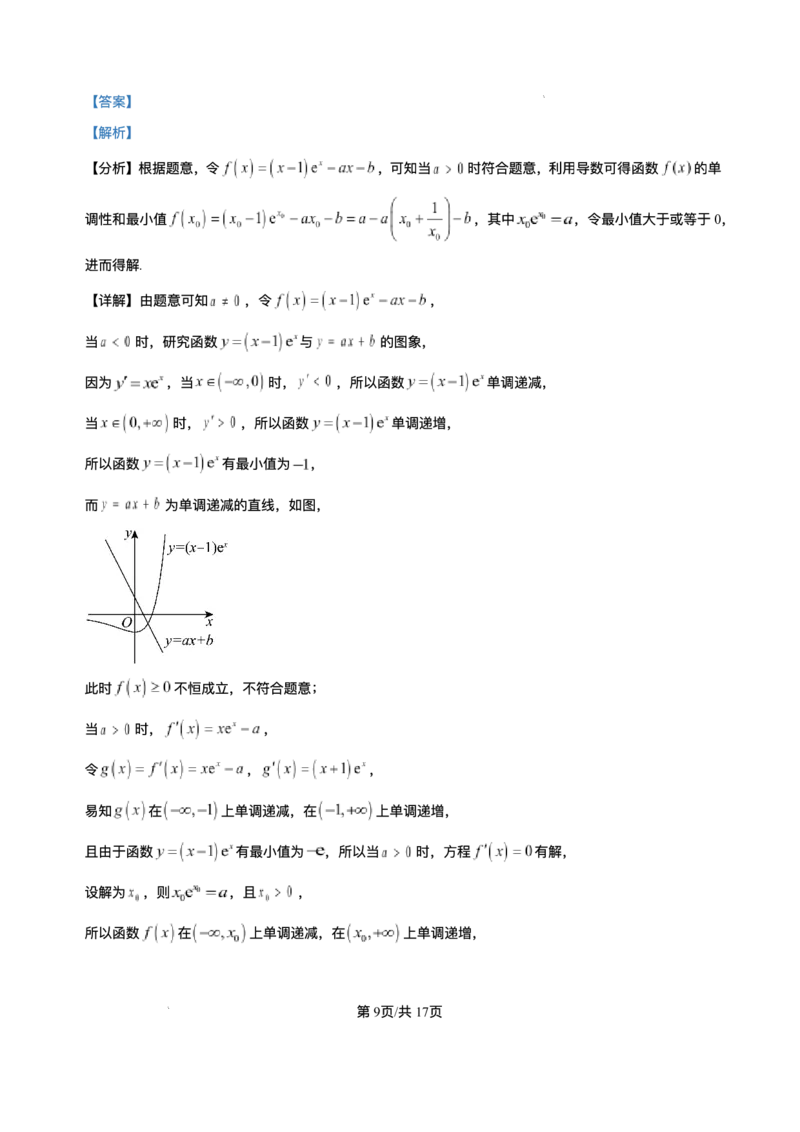
当 时,研究函数 与 的图象,
因为 ,当 时, ,所以函数 单调递减,
当 时, ,所以函数 单调递增,
所以函数 有最⼩值为 ,
⽽ 为单调递减的直线,如图,
此时 不恒成⽴,不符合题意;
当 时, ,
令 , ,
易知 在 上单调递减,在 上单调递增,
且由于函数 有最⼩值为 ,所以当 时,⽅程 有解,
设解为 ,则 ,且 ,
所以函数 在 上单调递减,在 上单调递增,
第9⻚/共17⻚
学科⽹(北京)股份有限公司所以 的最⼩值为 ,
由题意 恒成⽴,所以 ,
所以 ,
当且仅当 时取等号,此时 .
【点睛】关键点点睛:利⽤导数可知⽅程 有解,设解为 ,则 ,从⽽表示出 的
最⼩值,进⽽求解.
四、解答题:本题共5⼩题,共77分.解答应写出⽂字说明、证明过程或演算步骤.
15. 已知等差数列 的公差不为零, ,且 , , 成等⽐数列.
(1)求数列 的通项公式;
(2)设数列 的前 项和为 ,数列 的前 项和为 ,若 ,求 的最⼤值.
【答案】(1)
(2)98
【解析】
【分析】(1)利⽤等差数列性质 列⽅程,设公差 求解,舍去 ,再⽤通项公式求 .
(2)先求 ,对 裂项,⽤裂项相消法算 ,根据 解不等式求 最⼤值.
【⼩问1详解】
设 的公差为 ,则
,解得 或 (舍去)
即 的通项公式为 ;
【⼩问2详解】
第10⻚/共17⻚
学科⽹(北京)股份有限公司, ,
由 ,即 ,解得
的最⼤值为98.
16. 某种机械设备随着使⽤年限的增加,它的使⽤功能逐渐减退,使⽤价值逐年减少,通常把它使⽤价值逐
年减少的“量”换算成费⽤,称之为“失效费”.某种机械设备的使⽤年限 (单位:年)与失效费 (单位:
万元)的统计数据如下表所示:
使⽤年限 (单位:年) 2 4 5 6 8
失效费 (单位:万元) 3 4 5 6 7
(1)根据上表数据,计算 与 的相关系数 ,并说明 与 的线性相关性的强弱.
(已知: ,则认为 与 线性相关性很强; ,则认为与 线性相关性⼀般;
,则认为 与 线性相关性较弱)( 的结果精确到0.0001)
(2)求 关于 的线性回归⽅程,并估算该种机械设备使⽤10年的失效费.
附:样本 的相关系数 ,经验回归⽅程 的
斜率和截距的最⼩⼆乘估计分别为 , .
【答案】(1) ,线性相关性很强
(2) ,8.5万元
【解析】
【分析】(1)根据相关系数公式,分别求出变量的均值及和值,代⼊公式求得相关系数,并判断相关性强
弱即可;
第11⻚/共17⻚
学科⽹(北京)股份有限公司(2)根据第⼀问求得的值,结合线性回归⽅程求解公式求得参数 ,写出回归⽅程,并预测10年的失
效费即可.
【⼩问1详解】
由表知, , ,
,
, ,
,
故 ,认为 与 线性相关性很强;
【⼩问2详解】
由(1)知, ,
⼜ , ,
故 关于 的线性回归⽅程为 ,
当 时, ,即估算10年的失效费为8.5万元.
17. 据世界⽥联官⽅⽹站消息,原定于2023年5⽉ ⽇在中国⼴州举办的世界⽥联接⼒赛延期⾄2025
年4⽉⾄5⽉举⾏.据了解,甲、⼄、丙三⽀队伍将会参加2025年4⽉⾄5⽉在⼴州举⾏的 ⽶接⼒的
⻆逐.接⼒赛分为预赛、半决赛和决赛,只有预赛、半决赛都获胜才能进⼊决赛.已知甲队在预赛和半决赛中获
胜的概率分别为 和 ;⼄队在预赛和半决赛中获胜的概率分别为 和 ;丙队在预赛和半决赛中获胜的
概率分别为 和 .
(1)甲、⼄、丙三队中,谁进⼊决赛的可能性最⼤;
(2)设甲、⼄、丙三队中进⼊决赛的队伍数为 ,求 的分布列.
【答案】(1)⼄进⼊决赛的可能性最⼤
第12⻚/共17⻚
学科⽹(北京)股份有限公司(2)答案⻅解析
【解析】
【分析】(1)根据相互独⽴事件同时发⽣的概率公式计算得解;
(2)根据(1)及相互独⽴事件同时发⽣的概率公式计算,列出分布列.
【⼩问1详解】
甲队进⼊决赛的概率为 ,
⼄队进⼊决赛的概率为 ,
丙队进⼊决赛的概率为 ,
显然⼄队进⼊决赛的概率最⼤,所以⼄进⼊决赛的可能性最⼤.
【⼩问2详解】
由(1)可知:甲、⼄、丙三队进⼊决赛的概率分别为 ,
的可能取值为 ,
,
,
,
,
所以 的分布列为:
0 1 2 3
18. 已知 (e为⾃然对数的底数)
(1)求曲线 在点 处的切线⽅程;
第13⻚/共17⻚
学科⽹(北京)股份有限公司(2)求证:当 时, 恒成⽴;
(3)已知 ,如果当 时, 恒成⽴,求 的最⼤值.
【答案】(1)
(2)证明⻅解析 (3)
【解析】
【分析】(1)求导,然后利⽤导数的⼏何意义求切线⽅程;
(2)将不等式转化为 恒成⽴,构造函数 , ,然后求其最⼩值即可;
(3)将不等式转化为 恒成⽴,构造函数 ,然后求导研究其最值即可.
【⼩问1详解】
由已知 ,
则 , ,
所以曲线 在点 处的切线⽅程为 ;
【⼩问2详解】
,
设 , ,
则 ,所以 在 上单调递增,
所以 ,即 ,
所以当 时, 恒成⽴;
【⼩问3详解】
当 , 时, ,
令 , ,则 ,
令 ,则 ,所以 在 上单调递增,
第14⻚/共17⻚
学科⽹(北京)股份有限公司令 ,得 ,令 ,得 ,
当 ,即 时, 在 上单调递增,
所以 ,即 恒成⽴,
当 ,即 时, 在 上单调递减,在 上单调递增,
所以 ,不符合 恒成⽴,
所以 ,
所以当 时, 恒成⽴, 的最⼤值为 .
【点睛】关键点点睛:本题第三问的关键是等价转化为证明 在 上恒成⽴,然后再设
新函数,利⽤导数得到范围.
19. ⻢尔可夫链是因俄国数学家安德烈·⻢尔可夫得名,其过程具备“⽆记忆” 性质,即第 次状态的概
率分布只跟第 次的状态有关,为了避免就餐聚集和减少排队时间,某校开学后,⻝堂从开学第⼀天起,每
餐只推出即点即取的⽶饭套餐和⾯⻝套餐.已知某同学每天中午会在⻝堂提供的两种套餐中选择,已知他
第⼀天选择⽶饭套餐的概率为 ,⽽前⼀天选择了⽶饭套餐后⼀天继续选择⽶饭套餐的概率为 ,前⼀天
选择⾯⻝套餐后继续选择⾯⻝套餐的概率为 ,如此往复.
(1)求该同学第⼆天中午选择⽶饭套餐的概率;
(2)记该同学第 天选择⽶饭套餐的概率为 ;
①证明: 为等⽐数列;
②当 时, 恒成⽴,求 取值范围.
【答案】(1)
(2)①证明⻅解析;②
【解析】
【分析】(1)设 为“第 天选择⽶饭套餐”, 为“第 天选择⽶饭套餐”,根据条件求出
,再利⽤全概率公式,即可求解;
第15⻚/共17⻚
学科⽹(北京)股份有限公司(2)①设 为“第 天选择⽶饭套餐”,根据条件得到 ,
,利⽤全概率公式得到 ,即可证明结果;②由①得到 ,再对
分类讨论,利⽤单调性,即可求解.
【⼩问1详解】
设 为“第 天选择⽶饭套餐”, 为“第 天选择⽶饭套餐”,则 为“第1天不选择⽶饭套餐”,
根据题意 ,
由全概率公式得: .
【⼩问2详解】
①设 为“第 天选择⽶饭套餐”,则 ,
根据题意 ,
由全概率公式得: ,
因此 ,因为 ,
所以 是以 为⾸, 为公⽐的等⽐数列.
②由①可得 ,
当 为⼤于 的奇数时,
当 为正偶数时,
因此,当 时, ,所以 .
【点睛】关键点点晴,本题的关键在于第(2)中的第①问,利⽤全概率公式得到 ,
即可求解.
第16⻚/共17⻚
学科⽹(北京)股份有限公司第17⻚/共17⻚
学科⽹(北京)股份有限公司