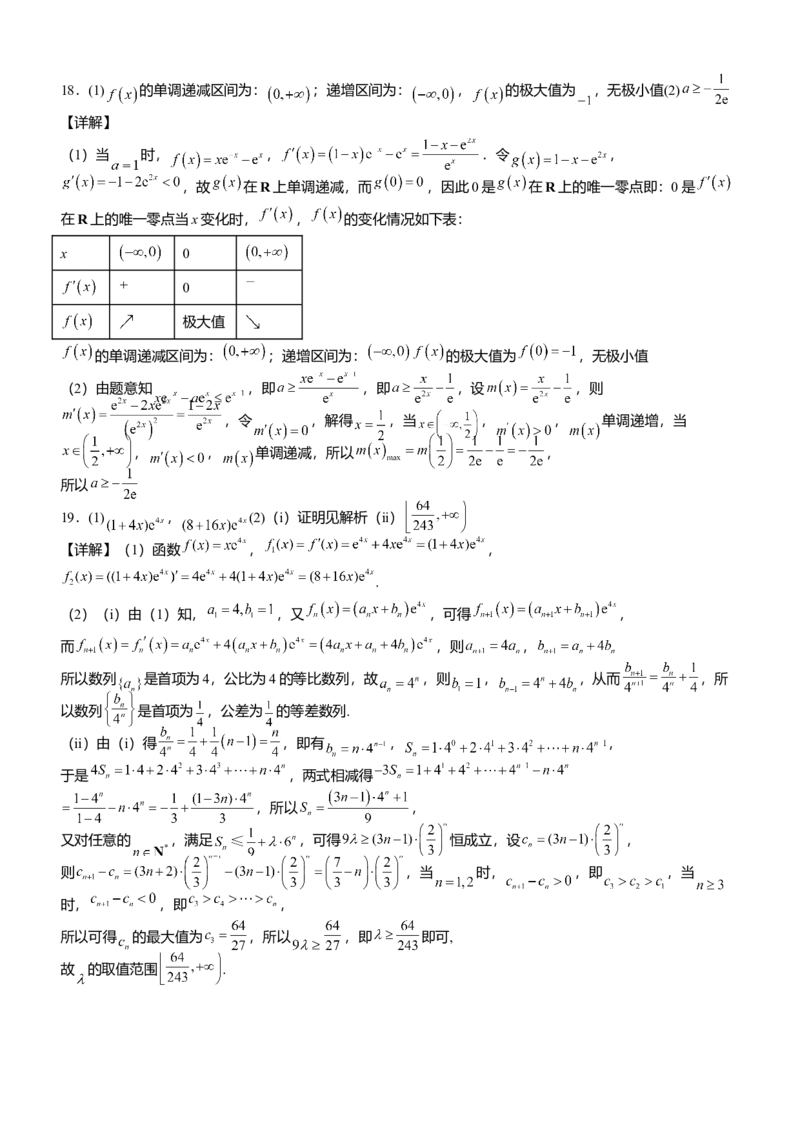文档内容
威远中学 2026 届高二下期半期考试
数 学
(命题人:第三小组)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,全卷满分150分,考试时间120分钟.
第Ⅰ卷 (选择题 共 58分)
选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合
题目要求的.
1.已知等差数列 的前 项和为 ,若 ,则 ( )
A. B. C.1 D.
2.在等比数列 中, , ,则 ( )
A.4 B.8 C.10 D.12
3.函数 的单调递增区间是( )
A. B. 和
C. D.
4.在等比数列{an}中,an>0,且a+a=1,a+a=9,则a+a 的值为( )
1 2 3 4 4 5
A.16 B.27 C.36 D.81
5.已知等差数列 的公差 , , ,记该数列的前n项和为 ,则 的最大值为
( )
A.20 B.24 C.36 D.40
6.已知函数 的图象如图所示,则不等式 的解集为( )
A. B. C. D.
7.已知数列 的前 项和为 ,且 , ,则 的值为( )
A.360 B.480 C.960 D.1280f(x)=xx,f' (x)为f(x)的导函数,则f' (1)=()
8.
A.1 B.-1 C.2 D.-2
二.多选题(本题共3个小题,每题6分,有多个选项,共18分)
9.已知数列 满足 ,则( )
A. B. 的前n项和为
C. 的前100项和为100 D. 的前30项和为357
10.已知 ,下列说法正确的是( )
A. 在 处的切线方程为 B. 的单调递减区间为
C. 的极大值为 D.方程 有两个不同的解
11.已知数列 满足 ,则下列结论正确的有( )
A. 为等比数列 B. 的通项公式为
C. 为递增数列 D. 的前n项和
第Ⅱ卷 (非选择题 共 92 分)
三.填空题:本大题共3小题,每小题5分,共15分,请把答案填在答题卡相应位置上.
12.已知数列 的前 项和为 , ,则 .
13.曲线 上的点到直线 的最短距离是 .
14.设 为数列 的前 项和,已知 , ,则 .
四、解答题(本大题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤)
15.(本小题满分13分)已知曲线 .(1)求曲线 在点 处的切线方程;
(2)求过点 且与曲线 相切的直线方程.
16.(本小题满分15分)已知数列 的前n项和 ,数列 的前n项和 .
(1)求 , 的通项公式;
(2)若 ,求 的前n项和 .
17.(本小题满分15分)已知数列 ,若 ,且 .
(1)证明数列 是等比数列,并求出 的通项公式;
(2)若 ,且数列 的前项和为 ,求 .18.(本小题满分17分)已知函数 .
(1)当 时,求 的单调区间和极值;
(2)若对任意 ,有 恒成立,求 的取值范围.
19.(本小题满分17分)已知函数 ,记 ,且 ,
(1)求 , ;
(2)设 , ,
(ⅰ)证明:数列 是等差数列;(ⅱ)数列 的前n项和为 ,且对任意的 ,满足 ,求 的取值范围.威远中学校 2026 届高二下半期考试数学试题参考答案 .
1.D解:由 ,根据等差数列的求和公式, ,
又 .故选:D
2.B解:由题意 ,且 ,所以 .故选:B.
3.C解:由题设, 且 ,可得 ,所以 递增区间为 .
故选:C
4.B解:∵a+a=1,a+a=9,∴q2=9.∴q=3(q=-3舍去)∴a+a=(a+a)q=27.故选:B
1 2 3 4 4 5 3 4
5.C解:等差数列 中,公差 ,即数列 是递减等差数列,
显然 ,而 ,且 ,解得 ,则 ,
,由 ,得 ,因此数列 前9项均为非负数,从第10项起均为负数,所以
的最大值为 .故选:C.
6.B解:由图象可知 在 上单调递增,在 上单调递减,
所以当 或 时, ;当 时, ;
而 等价于 ①,或 ②,由①得 或 ,则 ,
由②得 ,则 ,综上, .故选:B.
7.D解:当n为奇数, , ,当n为偶数, , ,
因此 , 的奇数项是以3为首项,3为公差的等差数列;
的偶数项是以 为首项,3为公差的等差数列,所以
.故选:D
1
对y=xx两边取对可得:ln y=lnxx =xlnx,对等式左右两边同时求导可得: y' =lnx+1,
y
8. A解:
即y' =(lnx+1)y=xx (lnx+1)f' (1)=1
9.AD解:当 时, ,当 时, ,
两式相减可得: ,所以 ,
显然当 时, 满足 ,故 ,故A正确;由等差数列求和公式知 的前 项和为
,故B错误;令 , 的前100项和为:
,故C错误;令 ,所以 的前30项和为:
,故D正确.故选:AD.10.BC解:对于A,由 ( ),得 , ,则 ,所以 在 处
的切线方程为 ,所以A错误,对于B,由 ,得 , ,所以 的单调递减区间
为 ,所以B正确,对于C,由 ,得 ,当 时, ,当 时, ,
所以当 时, 取得极大值 ,所以C正确,对于D,由C选项可知 的最大值为 ,且当
时, ,当 时, , 所以函数 与 的交点个数为1,所以
有1个解,所以D错误,故选:BC
11.ABD解:因为 ,所以 +3,所以 ,又因为
,所以数列 是以4为首项,2为公比的等比数列,故A正确;
,即 ,故B正确;因为
,因为 ,所以
,所以 ,所以 为递减数列,故C错误; ,则
,故D正确.故选:ABD.
12. 解:当 时, ,当 时, ,
此时 ,不符,故 .故答案为:
13. 解:与 平行的直线和 相切,则斜率为 ,因为 ,所以 ,令 ,解
方程得 ,代入直线方程得切点 ,则点 到直线的距离就是曲线 的点到直线 的最短
距离,
由点到直线的距离公式知 ,故答案为: .
14. 解: ,令 ,则 ,∴又
, ,∴ ;
①, ②,①减②得:,∴ ,∴ .
15.(1) (2) 和 .
解:(1) 当 时, ,
所以曲线 在点 处的切线方程为 ,即 .
(2)设切点坐标为 ,由(1)知切线的斜率为 ,故切线方程为 ,因为切
线过点 ,所以 ,即 ,所以 或 ,故过点 且
与曲线 相切的直线有两条,其方程分别是 和 ,即 和
.
16.(1) , (2)
解:(1)因为数列 的前n项和 ,所以当 时, ;当 时, ,
此时 满足上式,故 .因为数列 的前n项和 ,所以当 时, ;当 时,
,此时 满足上式,
故 .
(2)因为 ,所以
,则 ,两
式相减得 ,
化简得 .
17.(1)证明见解析, (2)
【详解】(1)因为 ,所以 ,又 ,所以 ,
所以 是以 为首项、 为公比的等比数列,所以 ,则 .
(2)由(1)可得 ,所以 ,
所以 .18.(1) 的单调递减区间为: ;递增区间为: , 的极大值为 ,无极小值(2)
【详解】
(1)当 时, , .令 ,
,故 在R上单调递减,而 ,因此0是 在R上的唯一零点即:0是
在R上的唯一零点当x变化时, , 的变化情况如下表:
x 0
0
极大值
的单调递减区间为: ;递增区间为: 的极大值为 ,无极小值
(2)由题意知 ,即 ,即 ,设 ,则
,令 ,解得 ,当 , , 单调递增,当
, , 单调递减,所以 ,
所以
19.(1) , (2)(ⅰ)证明见解析(ⅱ)
【详解】(1)函数 , ,
.
(2)(i)由(1)知, ,又 ,可得 ,
而 ,则 ,
所以数列 是首项为4,公比为4的等比数列,故 ,则 , ,从而 ,所
以数列 是首项为 ,公差为 的等差数列.
(ii)由(i)得 ,即有 , ,
于是 ,两式相减得
,所以 ,
又对任意的 ,满足 ,可得 恒成立,设 ,
则 ,当 时, ,即 ,当
时, ,即 ,
所以可得 的最大值为 ,所以 ,即 即可,
故 的取值范围 .