吉林地区2023-2024高三一模数学试题参考答案(1)_2023年11月_0211月合集_2024届吉林省吉林市高三上学期第一次模拟考试_吉林省吉林市2024届高三上学期第一次模拟考试数学

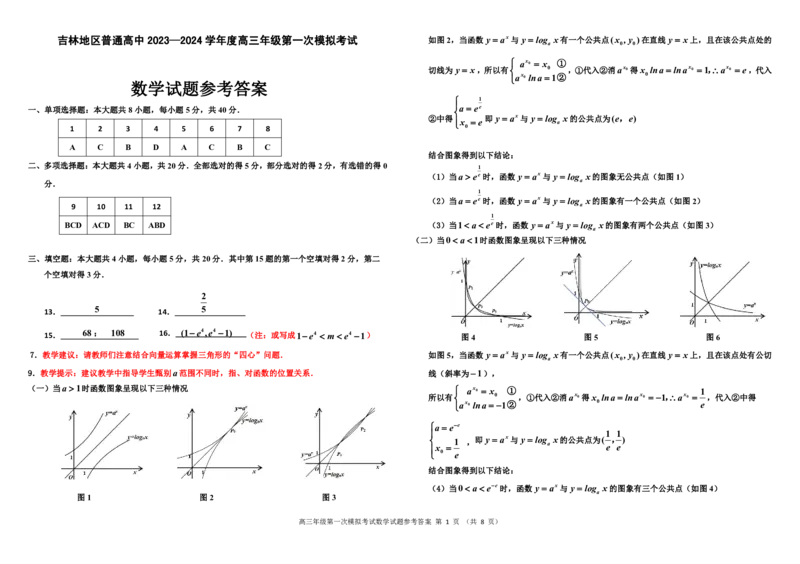
吉林地区普通高中 2023—2024 学年度高三年级第一次模拟考试 如图2，当函数 y  ax与 y  log x有一个公共点(x ,y )在直线 y  x上，且在该公共点处的
a 0 0
 ax 0  x ①
切线为 y  x，所以有 0 ，①代入②消ax 0得x lna  lnax 0 1，ax 0  e，代入
ax 0 lna 1② 0
数学试题参考答案
 1
一、单项选择题：本大题共8小题，每小题5分，共40分． 

a  ee
②中得 即 y  ax与 y  log x的公共点为(e，e)
 x  e a
1 2 3 4 5 6 7 8 0
A C B D A C B C
结合图象得到以下结论：
二、多项选择题：本大题共4小题，共20分．全部选对的得5分，部分选对的得2分，有选错的得0
1
（1）当a  ee时，函数 y  ax与 y  log x的图象无公共点（如图1）
分． a
1
（2）当a  ee时，函数 y  ax与 y  log x的图象有一个公共点（如图2）
9 10 11 12 a
1
BCD ACD BC ABD （3）当1 a  ee时，函数 y  ax与 y  log x的图象有两个公共点（如图3）
a
（二）当0 a 1时函数图象呈现以下三种情况
三、填空题：本大题共4小题，每小题5分，共20分．其中第15题的第一个空填对得2分，第二
个空填对得3分．
2
13． 5 14． 5
15． 68； 108 16． (1e4,e4 1) （注：或写成1e4  m  e4 1） 图4 图5 图6
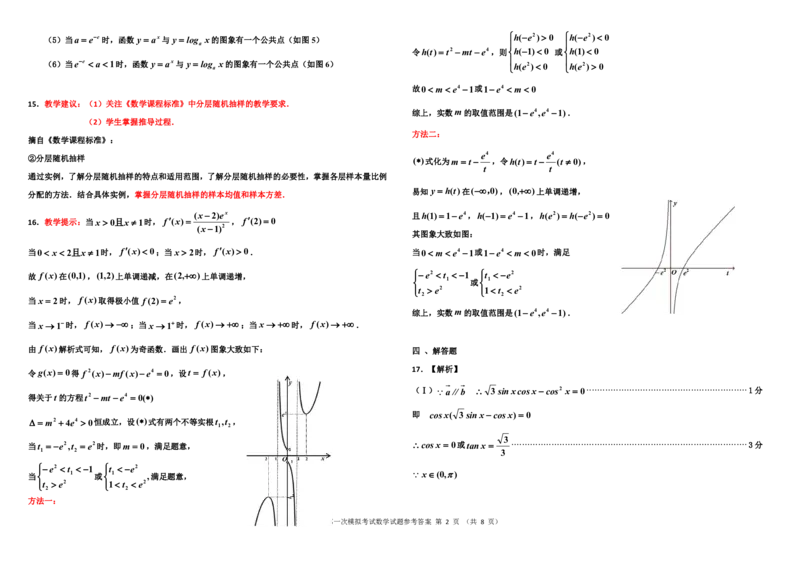
7．教学建议：请教师们注意结合向量运算掌握三角形的“四心”问题． 如图5，当函数 y  ax与 y  log x有一个公共点(x ,y )在直线 y  x上，且在该点处有公切
a 0 0
9．教学提示：建议教学中指导学生甄别a范围不同时，指、对函数的位置关系． 线（斜率为1），
（一）当a 1时函数图象呈现以下三种情况  ax 0  x ① 1
所以有 0 ，①代入②消ax 0得x lna  lnax 0  1，ax 0  ，代入②中得
ax 0 lna  1② 0 e
a  ee
 1 1
 1 ，即 y  ax与 y  log x的公共点为( ，)
x  a e e
 0 e
结合图象得到以下结论：
（4）当0 a  ee时，函数 y  ax与 y  log x的图象有三个公共点（如图4）
a
图1 图2 图3
高三年级第一次模拟考试数学试题参考答案 第 1 页 （共 8 页）（5）当a  ee时，函数 y  ax与 y  log x的图象有一个公共点（如图5） h(e2) 0 h(e2) 0
a  
令h(t) t2 mt e4，则h(1) 0 或h(1) 0
（6）当ee  a 1时，函数 y  ax与 y  log
a
x的图象有一个公共点（如图6）  h(e2) 0  h(e2) 0
故0 m  e4 1或1e4  m  0
15．教学建议：（1）关注《数学课程标准》中分层随机抽样的教学要求．
综上，实数m的取值范围是(1e4,e4 1)．
（2）学生掌握推导过程．
方法二：
摘自《数学课程标准》：
②分层随机抽样 ()式化为m  t
e4
，令h(t) t
e4
(t  0)，
t t
通过实例，了解分层随机抽样的特点和适用范围，了解分层随机抽样的必要性，掌握各层样本量比例
易知 y  h(t)在(，0)，(0,)上单调递增，
分配的方法．结合具体实例，掌握分层随机抽样的样本均值和样本方差．
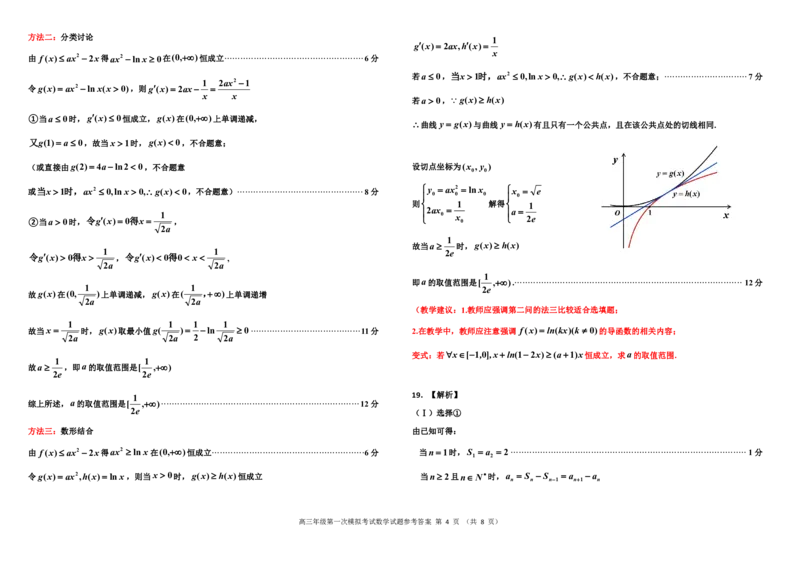
(x2)ex 且h(1)1e4，h(1) e4 1，h(e2) h(e2) 0
16．教学提示：当x  0且x 1时， f(x) ， f(2) 0
(x1)2
其图象大致如图：
当0 x  2且x 1时， f(x) 0；当x  2时， f(x) 0． 当0 m  e4 1或1e4  m  0时，满足
故 f(x)在(0,1)，(1,2)上单调递减，在(2,)上单调递增， e2  t  1 t  e2
 1 或 1
 t  e2  1 t  e2
2 2
当x  2时， f(x)取得极小值 f(2) e2，
综上，实数m的取值范围是(1e4,e4 1)．
当x 1时， f(x) ；当x 1时， f(x) ；当x  时， f(x) ．
由 f(x)解析式可知， f(x)为奇函数．画出 f(x)图象大致如下： 四 、解答题
17．【解析】
令g(x) 0得 f 2(x)mf (x)e4  0，设t  f(x)，
（Ⅰ） a // b  3sinxcosxcos2 x  0····························································1分
得关于t的方程t2 mt e4  0()
即 cosx( 3sinxcosx) 0
  m2 4e4  0恒成立，设()式有两个不等实根t ,t ，
1 2
3
当t  e2,t  e2时，即m  0，满足题意， cosx  0或tanx  ························································································3分
1 2 3
e2  t  1 t  e2
当 1 或 1 ,满足题意， x(0,)
 t  e2  1 t  e2
2 2
方法一：
高三年级第一次模拟考试数学试题参考答案 第 2 页 （共 8 页）   
x  或x  ···································································································5分  f(x)的单调递增区间是[  k,  k](kZ)·················································10分
2 6 3 6
（注：少一个解扣1分，没有角的范围表述扣1分.） （注：单调区间没有写成区间形式扣1分，没有注明k 的范围扣1分．）
方法二： a // b  3sinxcosxcos2 x  0·························································1分
18．【解析】
3 1cos2x
 sin2x  0
2 2 1
（Ⅰ）解： f(x) 2 (x  0)·············································································1分
x
 1
sin(2x ) ··································································································3分
6 2 所求切线斜率为 f(1) 1，切点为(1,2)··································································3分
  11 故所求切线方程为 y(2) (x1)，即x y1 0·················································5分
x(0,) 2x ( , )
6 6 6
（注：将切线方程表示成 y  x1也给分）
   5
2x  或2x 
（Ⅱ）方法一：分离变量
6 6 6 6
lnx
  由 f(x) ax2 2x得a  在(0,)恒成立··························································· 6分
x  或x  ···································································································5分 x2
6 2
（注：少一个解扣1分，没有角的范围表述扣1分.） lnx
令g(x) (x  0)，则a  g(x)
x2 max
1 1
（Ⅱ） f(x) ab  3sinxcosxcos2 x ················································6分 12lnx
2 2 g(x) ，g( e) 0·················································································8分
x3
3 1
 sin2x cos2x 当0 x  e 时，g(x) 0；当x  e 时，g(x) 0
2 2
故g(x)在(0, e)上单调递增，在( e,)上单调递减

 sin(2x )······················································································7分
6
1
故当x  e 时，g(x)取最大值 ···········································································11分
2e
  
令  2k 2x   2k (kZ)
2 6 2
1 1
故a  ，即a的取值范围是[ ,)······································································12分
2e 2e
 
  k x   k························································································9分
3 6
1
(注：表示成a  不扣分）
2e
高三年级第一次模拟考试数学试题参考答案 第 3 页 （共 8 页）方法二：分类讨论
1
g(x) 2ax,h(x)
x
由 f(x) ax2 2x得ax2 lnx  0在(0,)恒成立····················································6分
若a  0，当x 1时，ax2  0,lnx  0,g(x) h(x)，不合题意；·······························7分
1 2ax2 1
令g(x) ax2 lnx(x  0)，则g(x) 2ax 
x x
若a  0，g(x) h(x)
①当a  0时，g(x) 0恒成立，g(x)在(0,)上单调递减，
曲线 y  g(x)与曲线 y  h(x)有且只有一个公共点，且在该公共点处的切线相同.
又g(1) a  0，故当x 1时，g(x) 0，不合题意；
（或直接由g(2) 4aln2 0，不合题意 设切点坐标为(x , y )
0 0
或当x 1时，ax2  0,lnx  0,g(x) 0，不合题意）···············································8分 y  ax2  lnx x  e
 0 0 0  0
则 1 解得 1
 2ax  a 
②当a  0时，令g(x) 0得x  1 ，  0 x 0  2e
2a
1
故当a  时，g(x) h(x)
1 1 2e
令g(x) 0得x  ，令g(x) 0得0 x  ,
2a 2a
1
即a的取值范围是[ ,).····················································································· 12分
1 1 2e
故g(x)在(0, )上单调递减，g(x)在( ，)上单调递增
2a 2a
（教学建议：1.教师应强调第二问的法三比较适合选填题；
1 1 1 1
故当x  时，g(x)取最小值g( ) ln  0·········································11分 2.在教学中，教师应注意强调 f(x) ln(kx)(k  0)的导函数的相关内容；
2a 2a 2 2a
变式：若x[1,0],xln(12x)(a1)x恒成立，求a的取值范围.
1 1
故a  ，即a的取值范围是[ ,)
2e 2e
19．【解析】
1
综上所述，a的取值范围是[ ,)··········································································12分
2e （Ⅰ）选择①
方法三：数形结合 由已知可得：
由 f(x) ax2 2x得ax2  lnx在(0,)恒成立·························································6分 当n1时，S  a  2························································································1分
1 2
令g(x) ax2,h(x) lnx，则当x  0时，g(x) h(x)恒成立 当n 2且nN时，a  S  S  a a
n n n1 n1 n
高三年级第一次模拟考试数学试题参考答案 第 4 页 （共 8 页）a 1
a  2a 即 n1  2····························································································3分 nN  0T 1······································································ 12分
n1 n a 2n1 1 n
n
（注：若（Ⅰ）选择①，且未讨论a 1的情况，扣2分；
a
又 2 1不符合上式 但若（Ⅱ）运算正确，（Ⅱ）问正常赋分．）
a
1
关于劣构问题：
···················································································· 5分
2, n1,
劣构问题的常见形式：
a  
n 2n1,n 2且nN
（1）目标界定不明确的结构不良问题；
（2）具有多种解法、途径的结构不良问题；
选择②
（3）多个类似条件的结构不良问题；
S
n
 a
n1 （4）问题条件或数据冗余的结构不良问题；
S  S  S ·····································································································1分 （5）不同求解目标的结构不良问题．
n n1 n
条件的选择原则：
S
S
n1
 2S
n
即
S
n1  2··························································································3分
（1）应先分析所有条件，优先选择自己会做的、有把握的；
n
（2）在有把握的前提下，优先选择难度最小的；
又S  a  2
1 1
（3）在选择条件时，要通盘考虑条件对整个问题的影响．
{S
n
}是以2为首项，2为公比的等比数列．
教学建议：
S  22n1  2n (nN)····················································································5分 （1）引导学生从知识的习得记忆转向问题的解决、策略的选择，使数学应用在思维层面真正发生；
n
（2）注重渗透不良结构问题，采用开放式、互动式的教学方式，引导学生关注数学问题情境的变化；
（Ⅱ）由（Ⅰ）可知S a  2n，a  2n1
n n1 n2
（3）注重变式训练，提高学生的辨析能力和应变能力．
S 2n 1 1
b  n    ···································9分
n (a 1)(a 1) (2n 1)(2n1 1) 2n 1 2n1 1
n1 n2 20．【解析】
T  b b b b
n 1 2 3 n （Ⅰ）设Q 型芯片I级品该项指标的第70百分位数为a，
则该指标在80以下的概率为0.55，该指标在90以下的概率为0.8，因此该项指标的第70百分位数
1 1 1 1 1 1 1
(1 )(  )(  )(  )
3 3 7 7 15 2n 1 2n1 1 为a一定在[80,90)内
1
1 ·································································································11分 0.002100.005100.023100.025100.025（a80） 0.7
2n1 1
（也可以用0.02100.025（90a）10.7）
得a  86
高三年级第一次模拟考试数学试题参考答案 第 5 页 （共 8 页）所以Q 型芯片I级品该项指标的第70百分位数为86······················································3分  
2sin(C  ) 2 即 sin(C  ) 1··································································3分
6 6
（Ⅱ）当临界值c 65时，
  7  
Q 型芯片Ⅱ级品应用于A型手机的概率为0.01（7065） 0.05····································6分 C(0,) C  ( , ) C  
6 6 6 6 2
（Ⅲ）设直接将Q 型芯片Ⅰ级品、Ⅱ级品应用于A型、B型手机时，该芯片生产商支出为 y（万元），

C  ················································································································5分
3
y  700[0.002100.005（c50）]300[0.01100.03（60c）]
(注：没有角的范围表述扣1分.)
 4095.5c c[50,60]·····················································································8分

（Ⅱ）方法一：AB  BC ，C  ABC 为等边三角形
3
所以当50 c  56时， y 101，
AB  BC  AC  2
当c  56时， y 101，
CE  PE  x,BE  2 x,BP  m,m(0,2)
当56 c  60时， y 101·············································································10分 在BPE 中，由余弦定理得
PE2  BP2  BE2 2BPBEcosB······································································· 7分
综上：为降低芯片生产商的成本，当临界值c[50,56)时，选择方案二；
当临界值c  56时，选择方案一和方案二均可； 1
即x2  m2 (2 x)2 2m(2 x)
2
当临界值c(56,60]时，选择方案一．······························································12分
（注：以上三种情况，少一种扣1分，没有文字表述扣2分）
整理可得x 
m2 2m4
,m(0,2)·········································································8分
4m
21．【解析】 12 12
x  4m 6 2 (4m) 6  4 3 6
4m 4m
（Ⅰ）由正弦定理得
sinC(cosA 3sinA) sinB2sinA·································································1分 当且仅当m  42 3 时取等号
sinC(cosA 3sinA) sin(AC)2sinA 即BP  42 3时，CE取最小值4 3 6
sinC(cosA 3sinA) sinAcosC cosAsinC 2sinA 此时BE  84 3 ································································································10分
即 3sinAsinC  sinAcosC  2sinA 1  1 3
S  BPBEsin  (42 3)(84 3) 14 3 24.·················12分
PBE
2 3 2 2
A(0,) sinA 0

方法二：AB  BC ，C  ABC 为等边三角形
3
高三年级第一次模拟考试数学试题参考答案 第 6 页 （共 8 页）AB  BC  AC  2

当0 x  时， f(x) 0恒成立，即 f(x)单调递增，
CE  PE  x,BE  2 x,x(0,2) 2
m  0
2
设EPB ,(0, )
3  ex
当  x 时，m   恒成立
2 cosx
在BPE 中，由正弦定理得

PE BE ex 2ex sin(x )
sinEBP  sinEPB ··························································································7分 设g(x)  cosx ， g(x)  ex(cosx sinx)   4
cos2 x cos2 x
x 2 x 3  3
 令g(x) 0，则  x ，令g(x) 0，则  x 
即  sin 4 2 4
sin
3
 3 3
g(x)在( ， )上单调递减，在( ，)上单调递增
3 2 2 4 4
x  ,(0, )
整理可得 3 3 ········································································8分
sin
2 g(x)  g( 3 ) 2e 3 4  ，m  3
min 4 2e 4

当且仅当 时，x取最小值4 3 6 3
2 又m  0，0 m 
2e 4
3
当CE取最小值4 3 6时，BE  84 3 综上，m的取值范围 (0, 2e 4 ] ········································································5分
（注：（1）不写成区间形式也给分；（2）没写m  0扣1分）
 1
在RtBPE 中，BEP  ,BP  BE  42 3 ·················································10分
6 2 方法二：函数 f(x)在(0,)上单调递增
S  1 BPBEsin   1 (42 3)(84 3) 3 14 3 24.·················12分  f(x) ex mcosx  0在(0,)上恒成立（且不恒为0）
PBE
2 3 2 2
1 cosx
又m  0，  在(0,)上恒成立································································2分
m ex
22．【解析】
cosx
（Ⅰ）解： f(x) ex mcosx················································································1分 设h(x)
ex
方法一：函数 f(x)在(0,)上单调递增 
2sin(x )
sinxcosx
h(x)   4
 f(x) ex mcosx  0在(0，)上恒成立（且不恒为0）········································2分 ex ex
注：此处没取到等号，扣1分 3  3
令h(x) 0，则  x ，令h(x) 0，则  x 
4 2 4
高三年级第一次模拟考试数学试题参考答案 第 7 页 （共 8 页） 3 3 
h(x)在( ， )上单调递减，在( ，)上单调递增  f(x ) ex 0  sinx  cosx  sinx  2sin(x  )
2 4 4 0 0 0 0 0 4
3 2 3   3 
h(x)  h( )  又x ( ， )，x  (， )， 2sin(x  )(1,0)
min 4 3 0 4 2 0 4 4 0 4
2e 4
1 2 即1 f(x ) 0··································································································12分
   0
m 3
2e 4
3
又m  0，0 m  .
2e 4
3
综上，m的取值范围 (0, 2e 4 ] ·················································································5分
（Ⅱ）证明：m 1， f(x) ex  sinx， f(x) ex cosx
当x  0时，ex 1，cosx  1， f(x) ex cosx  0
 f(x)在(0，)上单调递增，即 f(x)在(0，)上无极值点·······································7分
当 x  0时，设u(x) f(x)，u(x) ex sinx  0恒成立
u(x)在(，0)上单调递增
u(  2 ) e   2  0，u( 3 4  ) e  3 4   2 2  1 3  1 2  0
e 4
3 
由零点存在性定理，存在唯一一个x ( ， )，使得u(x ) 0，即ex 0  cosx
0 4 2 0 0
当 x  x 时，u(x) 0， f(x) 0， f(x)在(，x )上单调递减
0 0
当x  x  0时，u(x) 0， f(x) 0， f(x)在(x ，0)上单调递增
0 0
 f(x)在(，)上存在唯一极小值点x ·······························································10分
0
3 
（注：此处x 所在区间必须是( ， )的子集，否则只给到10分位置）
0 4 2
高三年级第一次模拟考试数学试题参考答案 第 8 页 （共 8 页）