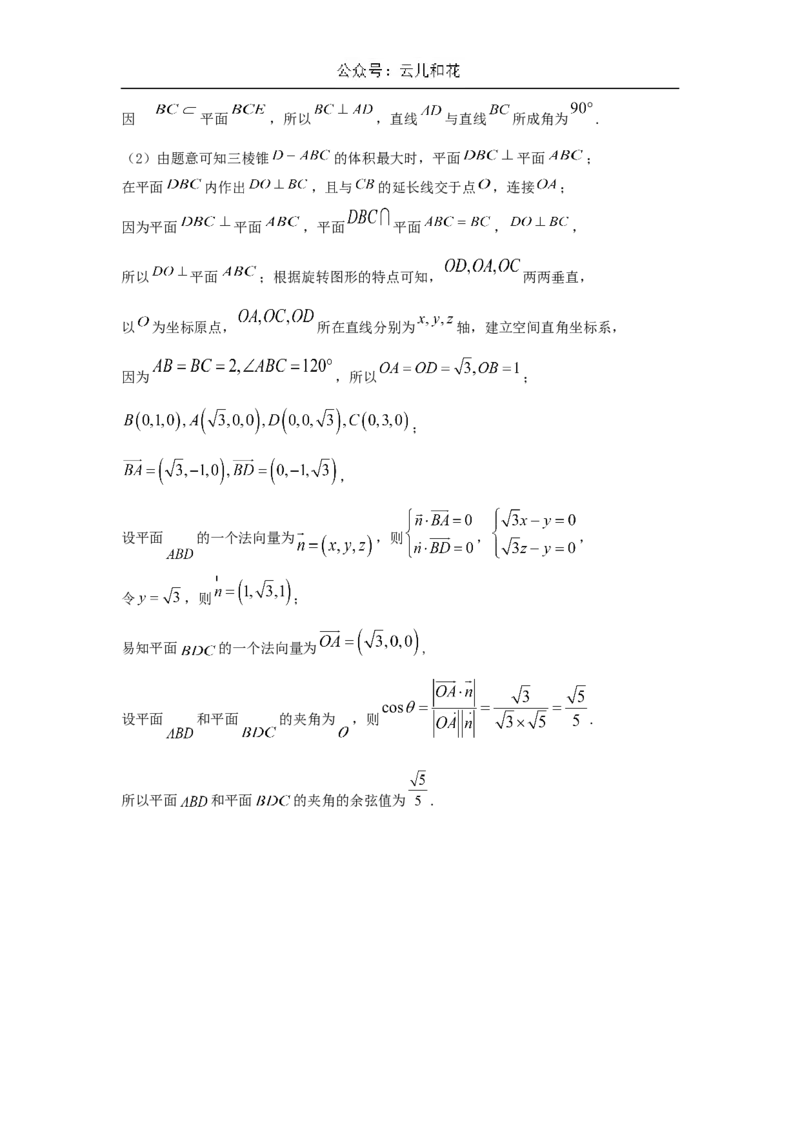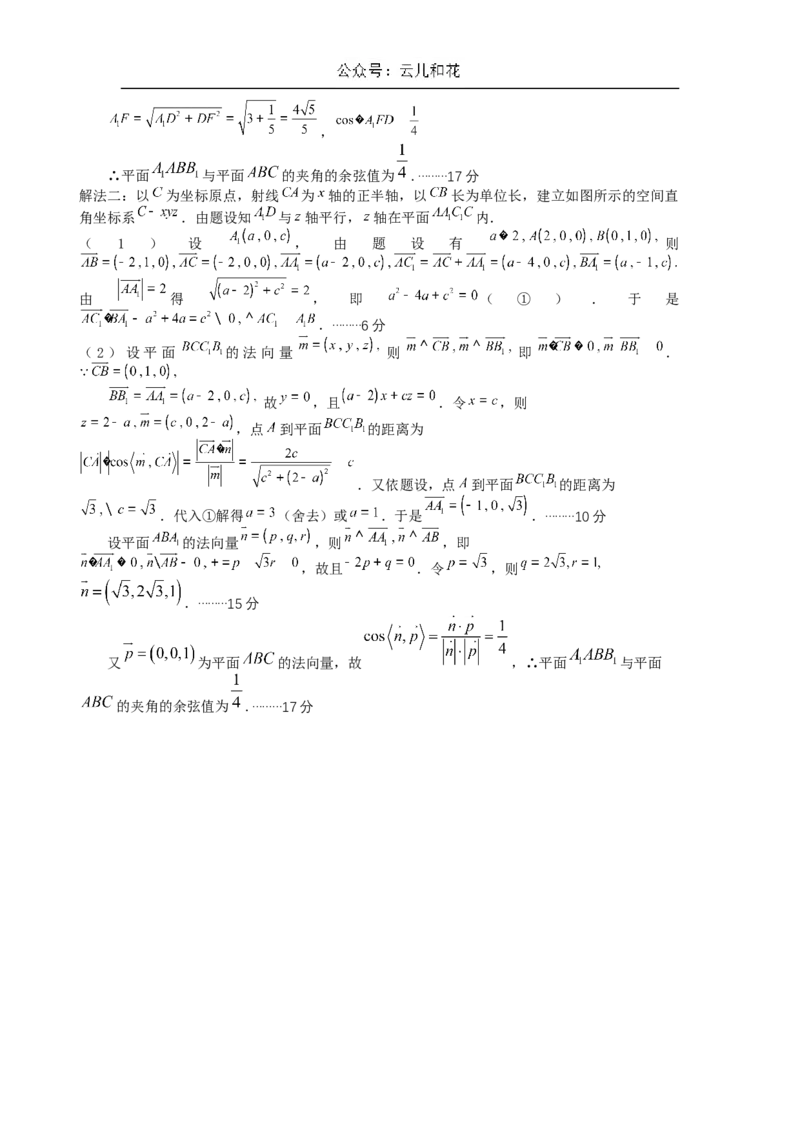文档内容
成都石室中学2024-2025学年度上期高2026届十月考试
数学试题
(满分150分,考试时间120分钟)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.
2.作答时,务必将答案写在答题卡上,写在试卷及草稿纸上无效.
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一
项是符合题目要求的.
1. 已知复数 满足: ,则复数 的共轭复数 的虚部为( )
A. B. -2 C. 2 D.
2. 在一个实验中,某种豚鼠被感染 病毒的概率均为 ,现采用随机模拟方法估计三只豚鼠中被感染
的概率:先由计算机产生出 之间整数值的随机数,指定1,2,3,4表示被感染,
5,6,7,8,9,0表示没有被感染.经随机模拟产生了如下20组随机数:
192 907 966 925 271 932 812 458 569 683
257 393 127 556 488 730 113 537 989 431
据此估计三只豚鼠都没被感染的概率为( )
A. 0.25 B. 0.4 C. 0.6 D.
0.75
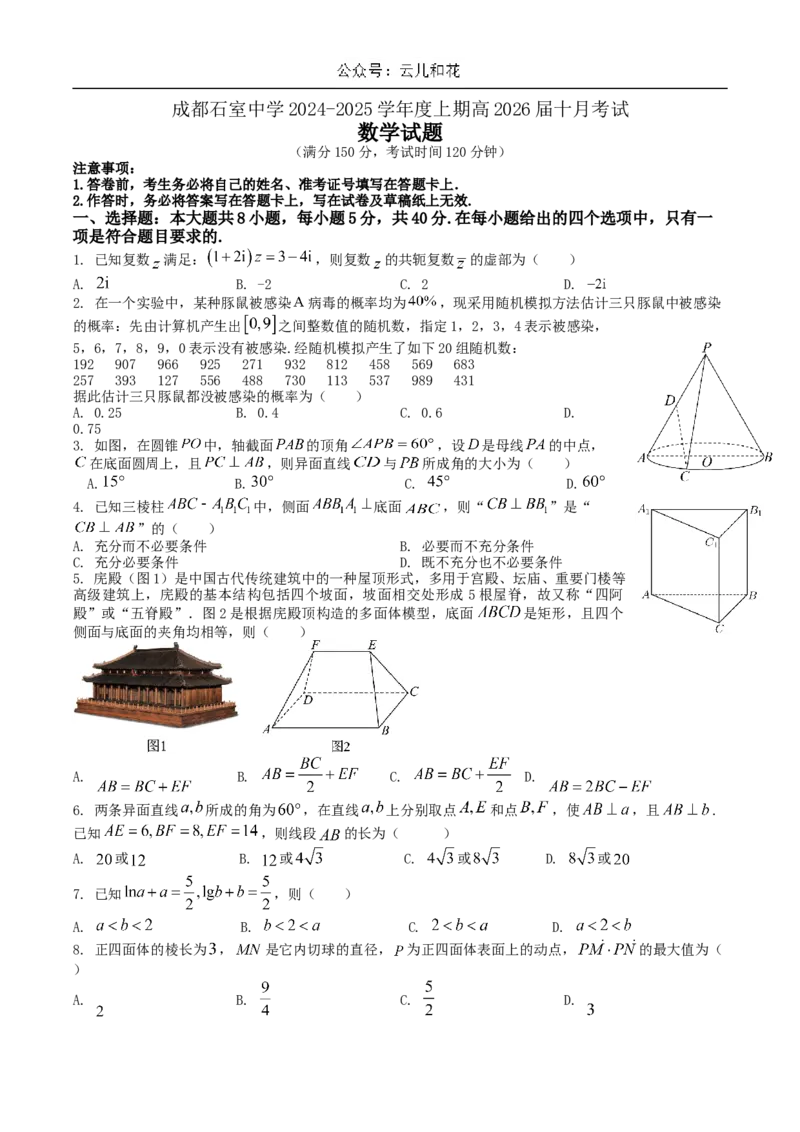
3. 如图,在圆锥 中,轴截面 的顶角 ,设 是母线 的中点,
在底面圆周上,且 ,则异面直线 与 所成角的大小为( )
A. B. C. D.
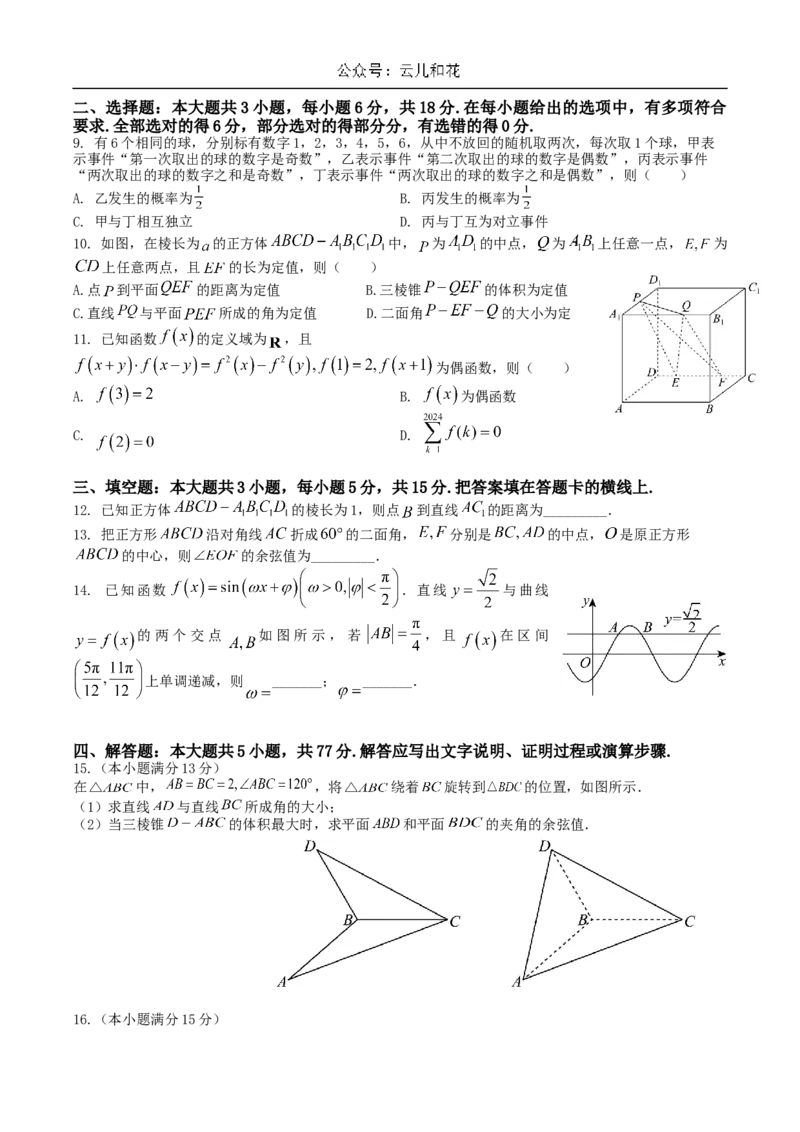
4. 已知三棱柱 中,侧面 底面 ,则“ ”是“
”的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
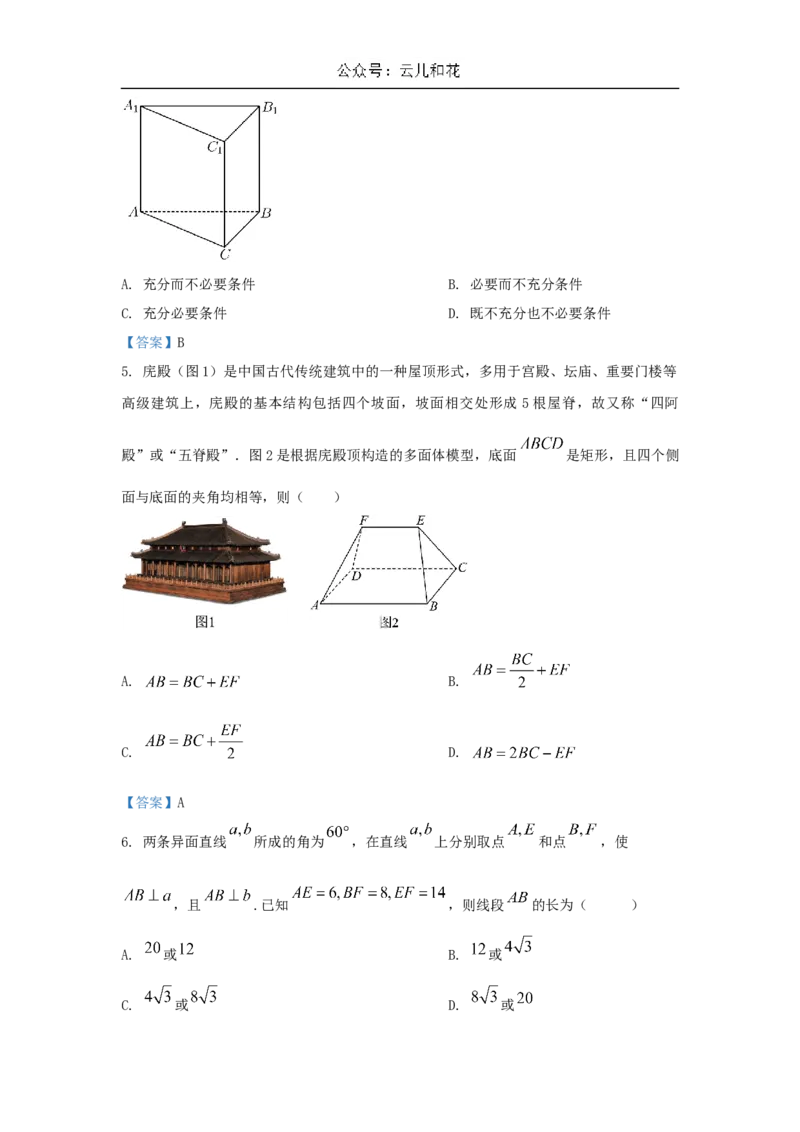
5. 庑殿(图1)是中国古代传统建筑中的一种屋顶形式,多用于宫殿、坛庙、重要门楼等
高级建筑上,庑殿的基本结构包括四个坡面,坡面相交处形成 5根屋脊,故又称“四阿
殿”或“五脊殿”.图2是根据庑殿顶构造的多面体模型,底面 是矩形,且四个
侧面与底面的夹角均相等,则( )
A. B. C. D.
6. 两条异面直线 所成的角为 ,在直线 上分别取点 和点 ,使 ,且 .
已知 ,则线段 的长为( )
A. 或 B. 或 C. 或 D. 或
7. 已知 ,则( )
A. B. C. D.
8. 正四面体的棱长为 , 是它内切球的直径, 为正四面体表面上的动点, 的最大值为(
)
A. B. C. D.二、选择题:本大题共 3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 有6个相同的球,分别标有数字1,2,3,4,5,6,从中不放回的随机取两次,每次取1个球,甲表
示事件“第一次取出的球的数字是奇数”,乙表示事件“第二次取出的球的数字是偶数”,丙表示事件
“两次取出的球的数字之和是奇数”,丁表示事件“两次取出的球的数字之和是偶数”,则( )
A. 乙发生的概率为 B. 丙发生的概率为
C. 甲与丁相互独立 D. 丙与丁互为对立事件
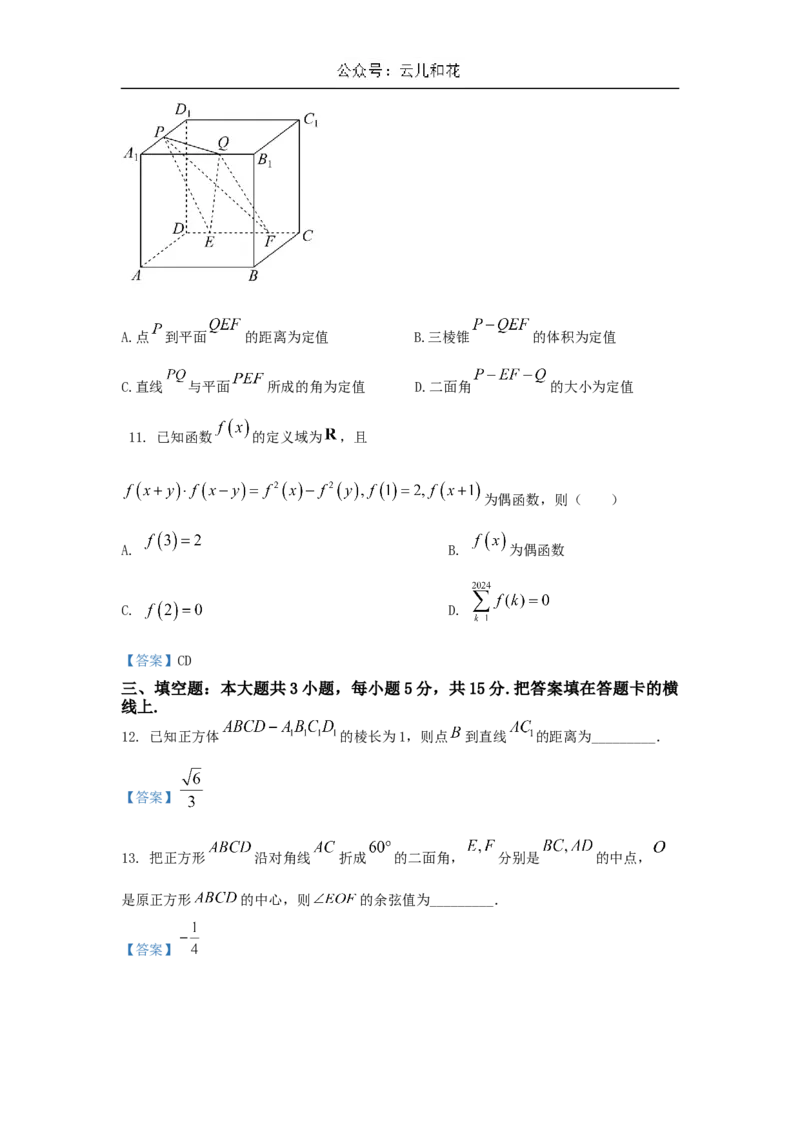
10. 如图,在棱长为 的正方体 中, 为 的中点, 为 上任意一点, 为
上任意两点,且 的长为定值,则( )
A.点 到平面 的距离为定值 B.三棱锥 的体积为定值
C.直线 与平面 所成的角为定值 D.二面角 的大小为定
11. 已知函数 的定义域为 ,且
为偶函数,则( )
A. B. 为偶函数
C. D.
三、填空题:本大题共3小题,每小题5分,共15分.把答案填在答题卡的横线上.
12. 已知正方体 的棱长为1,则点 到直线 的距离为_________.
13. 把正方形 沿对角线 折成 的二面角, 分别是 的中点, 是原正方形
的中心,则 的余弦值为_________.
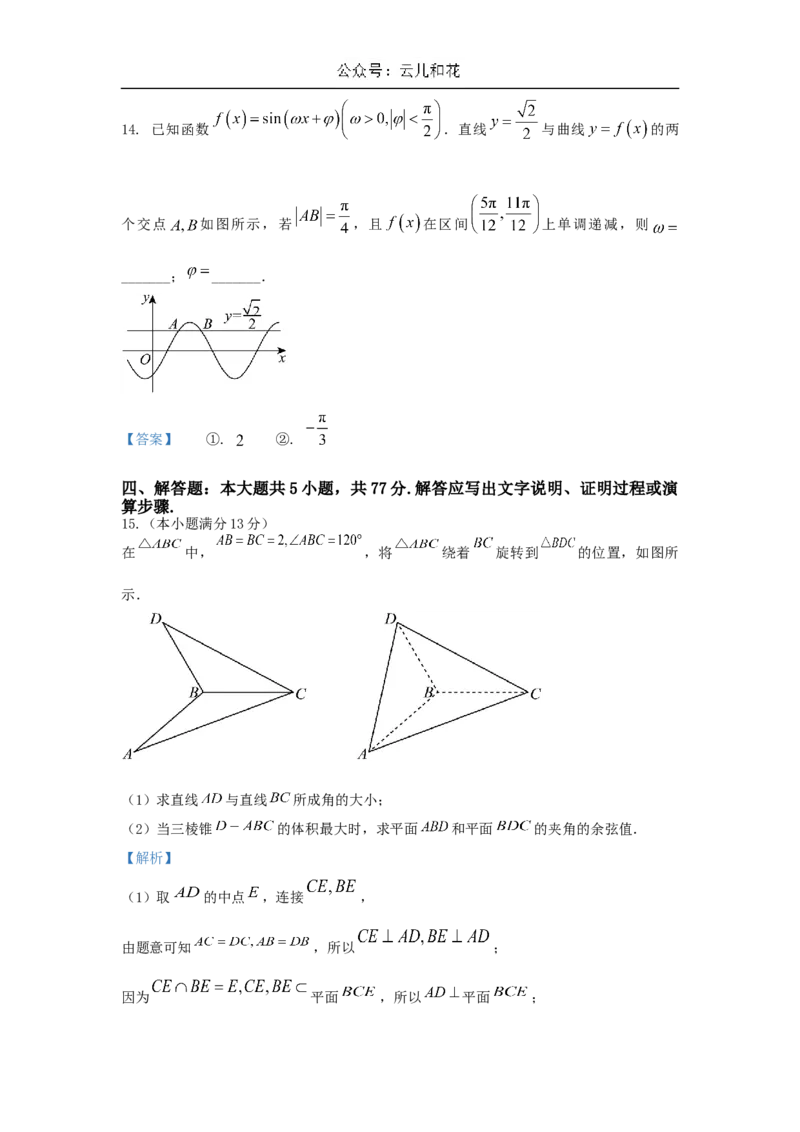
14. 已知函数 .直线 与曲线
的两个交点 如图所示,若 ,且 在区间
上单调递减,则 _______; _______.
四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(本小题满分13分)
在 中, ,将 绕着 旋转到 的位置,如图所示.
(1)求直线 与直线 所成角的大小;
(2)当三棱锥 的体积最大时,求平面 和平面 的夹角的余弦值.
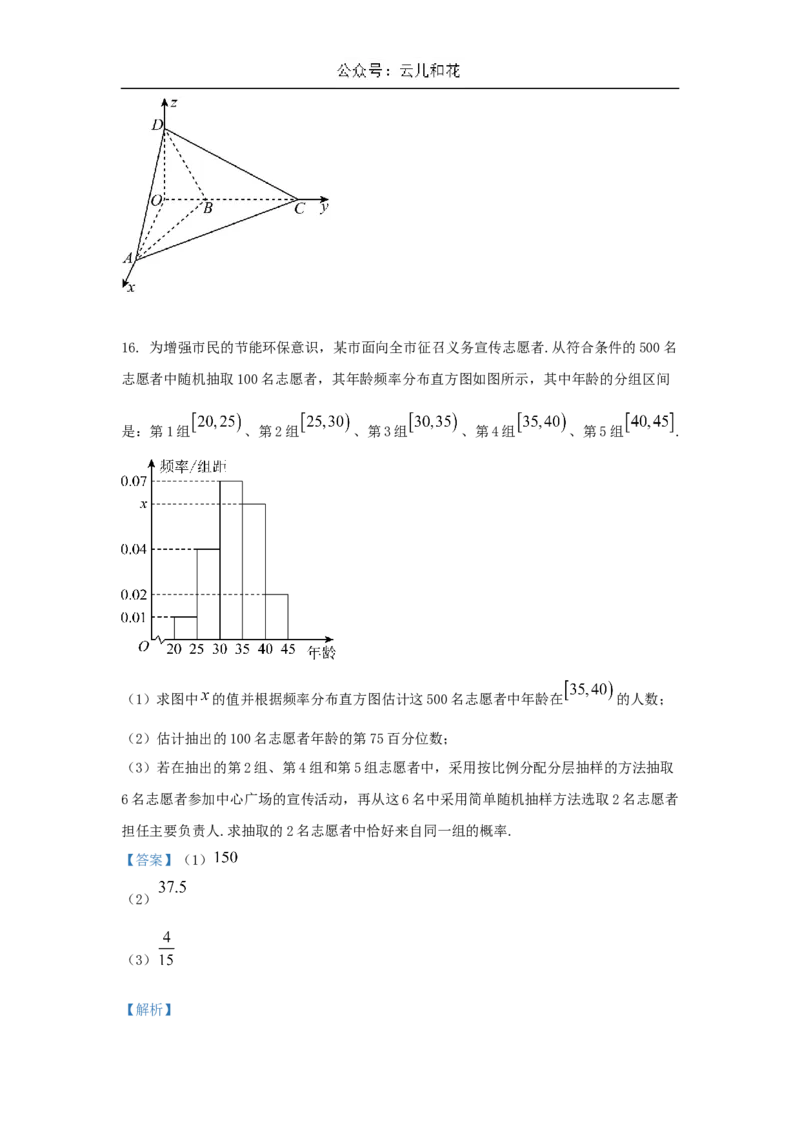
16.(本小题满分15分)为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的500名志愿者中随机抽取
100名志愿者,其年龄频率分布直方图如图所示,其中年龄的分组区间是:第1组 、第2组
、第3组 、第4组 、第5组 .
(1)求图中 的值并根据频率分布直方图估计这500名志愿者中年
龄在 的人数;
(2)估计抽出的100名志愿者年龄的第75百分位数;
(3)若在抽出的第2组、第4组和第5组志愿者中,采用按比例分
配分层抽样的方法抽取6名志愿者参加中心广场的宣传活动,再从这
6名中采用简单随机抽样方法选取2名志愿者担任主要负责人.求抽
取的2名志愿者中恰好来自同一组的概率.
17.(本小题满分15分)
在 中,角 的对边分别是 ,且 .
(1)求角 的大小;
(2)若 , 为 边上的一点, ,且______,求 的面积.
请在下列两个条件中选择一个作为条件补充在横线上,并解决问题.
① 是 的平分线;② 为线段 的中点.
(注:如果选择多个条件分别解答,则按第一个解答记分.)
18.(本小题满分17分)
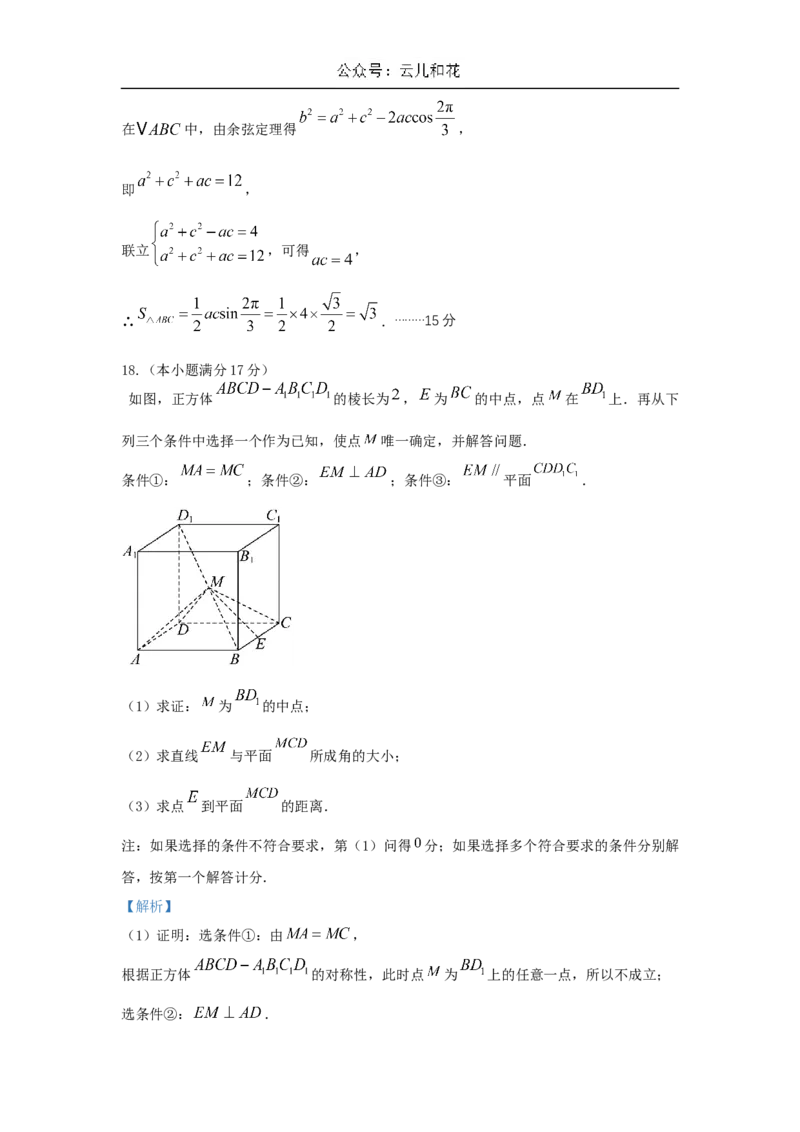
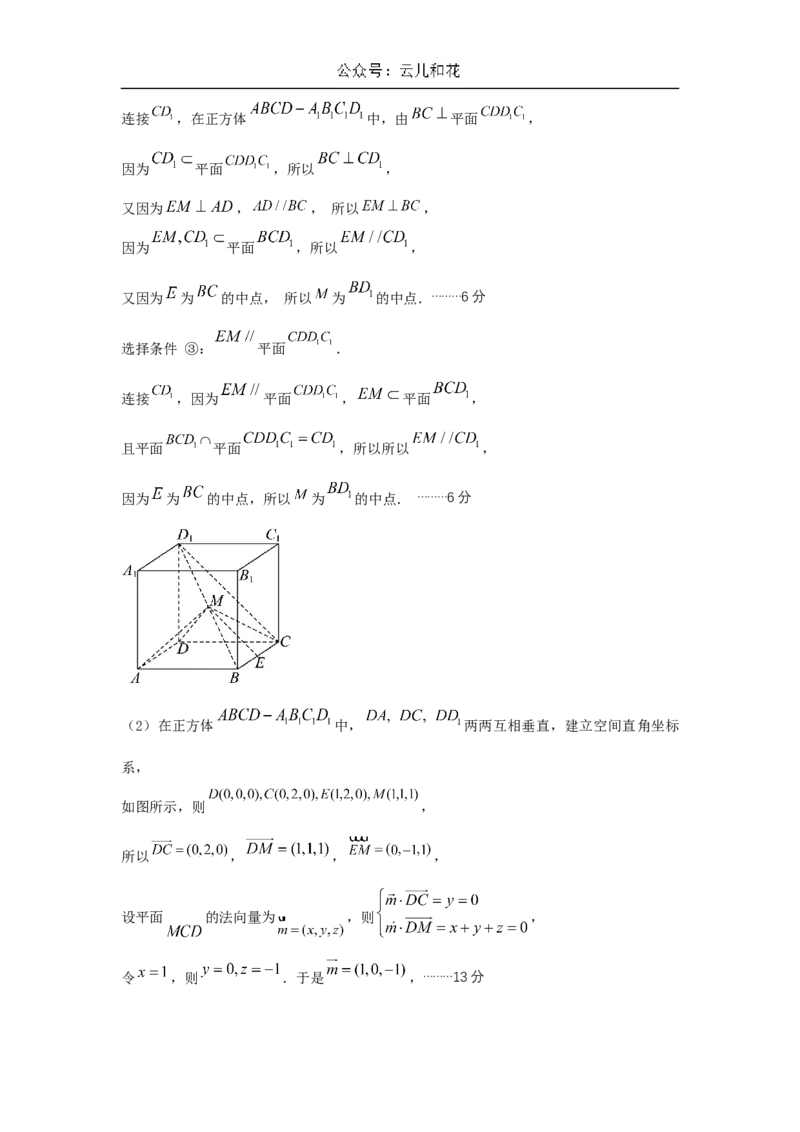
如图,正方体 的棱长为 , 为 的中点,点
在 上.再从下列三个条件中选择一个作为已知,使点 唯一确
定,并解答问题.条件①: ;条件②: ;条件③: 平面 .
(1)求证: 为 的中点;
(2)求直线 与平面 所成角的大小;
(3)求点 到平面 的距离.
注:如果选择的条件不符合要求,第(1)问得 分;如果选择多个符合要求的条件分别解答,按第一个解
答计分.
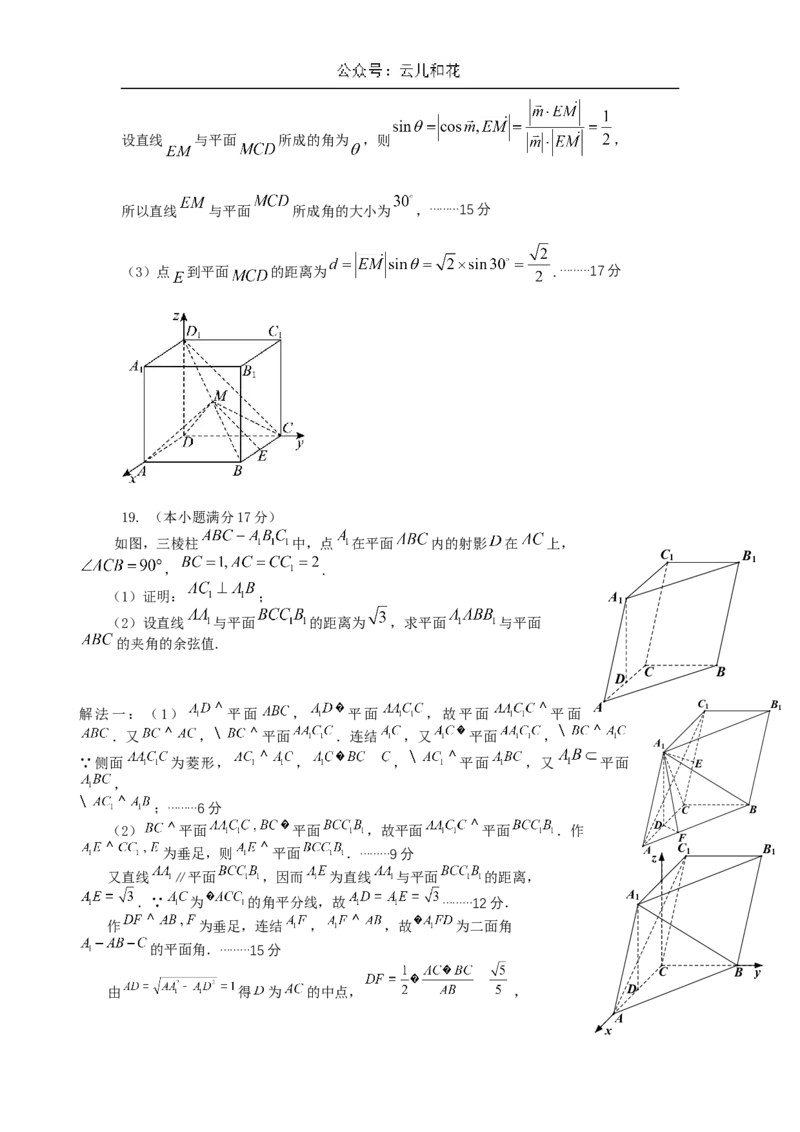
19. (本小题满分17分)
如图,三棱柱 中,点 在平面 内的射影 在 上,
, .
(1)证明: ;
(2)设直线 与平面 的距离为 ,求平面 与平面 的夹角的余弦值.成都石室中学2024-2025学年度上期高2026届10月月考
数学试题
(满分150分,考试时间120分钟)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.
2.作答时,务必将答案写在答题卡上,写在试卷及草稿纸上无效.
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选
项中,只有一项是符合题目要求的.
1. 已知复数 满足: ,则复数 的共轭复数 的虚部为( )
A. B. -2 C. 2 D.
【答案】C
2. 在一个实验中,某种豚鼠被感染 病毒的概率均为 ,现采用随机模拟方法估计三
只豚鼠中被感染的概率:先由计算机产生出 之间整数值的随机数,指定1,2,3,4
表示被感染,5,6,7,8,9,0表示没有被感染.经随机模拟产生了如下20组随机数:
192 907 966 925 271 932 812 458 569 683
257 393 127 556 488 730 113 537 989 431
据此估计三只豚鼠都没被感染的概率为( )
A. 0.25 B. 0.4 C. 0.6 D. 0.75
【答案】A
3. 如图,在圆锥 中,轴截面 的顶角 ,设 是母线 的中点,
在底面圆周上,且 ,则异面直线 与 所成角的大小为( C )
A. B. C. D.
4. 已知三棱柱 中,侧面 底面 ,则“ ”是“
”的( )A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
【答案】B
5. 庑殿(图1)是中国古代传统建筑中的一种屋顶形式,多用于宫殿、坛庙、重要门楼等
高级建筑上,庑殿的基本结构包括四个坡面,坡面相交处形成 5根屋脊,故又称“四阿
殿”或“五脊殿”.图2是根据庑殿顶构造的多面体模型,底面 是矩形,且四个侧
面与底面的夹角均相等,则( )
A. B.
C. D.
【答案】A
6. 两条异面直线 所成的角为 ,在直线 上分别取点 和点 ,使
,且 .已知 ,则线段 的长为( )
A. 或 B. 或
C. 或 D. 或【答案】B
7. 已知 ,则( )
A. B.
C. D.
【答案】D
8. 正四面体的棱长为 , 是它内切球的直径, 为正四面体表面上的动点,
的最大值为( )
A. B. C. D.
【答案】D
二、选择题:本大题共 3小题,每小题6分,共18分.在每小题给出的选项中,
有多项符合要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 有6个相同的球,分别标有数字1,2,3,4,5,6,从中不放回的随机取两次,每次
取1个球,甲表示事件“第一次取出的球的数字是奇数”,乙表示事件“第二次取出的球
的数字是偶数”,丙表示事件“两次取出的球的数字之和是奇数”,丁表示事件“两次取
出的球的数字之和是偶数”,则( )
A. 乙发生的概率为 B. 丙发生的概率为
C. 甲与丁相互独立 D. 丙与丁互为对立事件
【答案】ACD
10. 如图,在棱长为 的正方体 中, 为 的中点, 为 上任
意一点, 为 上任意两点,且 的长为定值,则( ABD )A.点 到平面 的距离为定值 B.三棱锥 的体积为定值
C.直线 与平面 所成的角为定值 D.二面角 的大小为定值
11. 已知函数 的定义域为 ,且
为偶函数,则( )
A. B. 为偶函数
C. D.
【答案】CD
三、填空题:本大题共 3小题,每小题5分,共15分.把答案填在答题卡的横
线上.
12. 已知正方体 的棱长为1,则点 到直线 的距离为_________.
【答案】
13. 把正方形 沿对角线 折成 的二面角, 分别是 的中点,
是原正方形 的中心,则 的余弦值为_________.
【答案】14. 已知函数 .直线 与曲线 的两
个交点 如图所示,若 ,且 在区间 上单调递减,则
_______; _______.
【答案】 ①. ②.
四、解答题:本大题共 5小题,共77分.解答应写出文字说明、证明过程或演
算步骤.
15.(本小题满分13分)
在 中, ,将 绕着 旋转到 的位置,如图所
示.
(1)求直线 与直线 所成角的大小;
(2)当三棱锥 的体积最大时,求平面 和平面 的夹角的余弦值.
【解析】
(1)取 的中点 ,连接 ,
由题意可知 ,所以 ;
因为 平面 ,所以 平面 ;为
因 平面 ,所以 ,直线 与直线 所成角为 .
(2)由题意可知三棱锥 的体积最大时,平面 平面 ;
在平面 内作出 ,且与 的延长线交于点 ,连接 ;
因为平面 平面 ,平面 平面 , ,
所以 平面 ;根据旋转图形的特点可知, 两两垂直,
以 为坐标原点, 所在直线分别为 轴,建立空间直角坐标系,
因为 ,所以 ;
;
,
设平面 的一个法向量为 ,则 , ,
令 ,则 ;
易知平面 的一个法向量为 ,
设平面 和平面 的夹角为 ,则 .
所以平面 和平面 的夹角的余弦值为 .16. 为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的500名
志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,其中年龄的分组区间
是:第1组 、第2组 、第3组 、第4组 、第5组 .
(1)求图中 的值并根据频率分布直方图估计这500名志愿者中年龄在 的人数;
(2)估计抽出的100名志愿者年龄的第75百分位数;
(3)若在抽出的第2组、第4组和第5组志愿者中,采用按比例分配分层抽样的方法抽取
6名志愿者参加中心广场的宣传活动,再从这6名中采用简单随机抽样方法选取2名志愿者
担任主要负责人.求抽取的2名志愿者中恰好来自同一组的概率.
【答案】(1)
(2)
(3)
【解析】(1)由直方图知: ,可得 ,
∴500名志愿者中年龄在 的人数为 人. ………2分
(2)因为 ,
,
所以第 百分位数在 区间内,若该数为 ,
∴ ,解得 .………6分
(3)由题设,第2组、第4组和第5组的频率之比为 ,知6名志愿者有2名来自
,3名来自 ,1名来自 , ………8分
不妨设第2组、第4组和第5组抽取的志愿者为 ,
则抽取两人的基本事件有 ,
,共15个,………12分
∴抽取的2名志愿者中恰好来自同一组的概率 .………13分
17.(本小题满分15分)
在 中,角 的对边分别是 ,且 .
(1)求角 的大小;
(2)若 , 为 边上的一点, ,且______,求 的面积.
请在下列两个条件中选择一个作为条件补充在横线上,并解决问题.
① 是 的平分线;② 为线段 的中点.
(注:如果选择多个条件分别解答,则按第一个解答记分.)
【解析】
(1)由正弦定理知, ,∵ ,
代入上式得 ,………3分
∵ ,∴ , ,
∵ ,∴ .………5分
(2)若选①:由 平分 得, ,
∴ ,即 .………8分
在 中,由余弦定理得 ,
又 ,∴ ,………10分
联立 得 ,
解得 , (舍去),
∴ .………15分
若选②:因为 ,
所以 ,
即 ,得 ,………10分在 中,由余弦定理得 ,
即 ,
联立 ,可得 ,
∴ .………15分
18.(本小题满分17分)
如图,正方体 的棱长为 , 为 的中点,点 在 上.再从下
列三个条件中选择一个作为已知,使点 唯一确定,并解答问题.
条件①: ;条件②: ;条件③: 平面 .
(1)求证: 为 的中点;
(2)求直线 与平面 所成角的大小;
(3)求点 到平面 的距离.
注:如果选择的条件不符合要求,第(1)问得 分;如果选择多个符合要求的条件分别解
答,按第一个解答计分.
【解析】
(1)证明:选条件①:由 ,
根据正方体 的对称性,此时点 为 上的任意一点,所以不成立;
选条件②: .连接 ,在正方体 中,由 平面 ,
因为 平面 ,所以 ,
又因为 , , 所以 ,
因为 平面 ,所以 ,
又因为 为 的中点, 所以 为 的中点.………6分
选择条件 ③: 平面 .
连接 ,因为 平面 , 平面 ,
且平面 平面 ,所以所以 ,
因为 为 的中点,所以 为 的中点. ………6分
(2)在正方体 中, 两两互相垂直,建立空间直角坐标
系,
如图所示,则 ,
所以 , , ,
设平面 的法向量为 ,则 ,
令 ,则 .于是 ,………13分设直线 与平面 所成的角为 ,则 ,
所以直线 与平面 所成角的大小为 ,………15分
(3)点 到平面 的距离为 .………17分
19. (本小题满分17分)
如图,三棱柱 中,点 在平面 内的射影 在 上,
C B
1 1
, .
(1)证明: ; A
1
(2)设直线 与平面 的距离为 ,求平面 与平面
的夹角的余弦值.
C B
D
解法一:(1) 平面 , 平面 ,故平面 平面 A C 1 B 1
.又 , 平面 .连结 ,又 平面 ,
A
1
∵侧面 为菱形, , , 平面 ,又 平面 E
,
;………6分 C B
D
(2) 平面 平面 ,故平面 平面 .作
F
为垂足,则 平面 .………9分 A z C 1 B 1
又直线 ∥平面 ,因而 为直线 与平面 的距离,
A
.∵ 为 的角平分线,故 ………12分. 1
作 为垂足,连结 , ,故 为二面角
的平面角.………15分
C B y
由 得 为 的中点, , D
A
x,
∴平面 与平面 的夹角的余弦值为 .………17分
解法二:以 为坐标原点,射线 为 轴的正半轴,以 长为单位长,建立如图所示的空间直
角坐标系 .由题设知 与 轴平行, 轴在平面 内.
( 1 ) 设 , 由 题 设 有 则
由 得 , 即 ( ① ) . 于 是
.………6分
(2)设平面 的法向量 则 即 .
故 ,且 .令 ,则
,点 到平面 的距离为
.又依题设,点 到平面 的距离为
.代入①解得 (舍去)或 .于是 .………10分
设平面 的法向量 ,则 ,即
,故且 .令 ,则
.………15分
又 为平面 的法向量,故 ,∴平面 与平面
的夹角的余弦值为 .………17分