云南师范大学附属中学2025届高三高考适应性月考卷（四）数学答案_2024-2025高三（6-6月题库）_2024年10月试卷_1025云南师范大学附属中学2025届高三高考适应性月考卷（四）

数学参考答案 一、单项选择题（本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只 有一项符合题目要求） 题号 1 2 3 4 5 6 7 8 答案 B D A B D C B A 【解析】 1．复数Z i2024 i2025 1i，则Z 的共轭复数Z 1i，所以Z 的虚部为−1，故选B．   1   π     2．∵ a 在b 上的投影向量为 b ，∴ a 与b 的夹角为 ， |a2b|254ab3，则 2 3   |a2b| 3，故选D． 3．设g(x)sinxx，由于g(x)g(x)，故g(x)为R上的奇函数，且g(x)的图象关于原点 对称．又 f(x)g(x1)1，所以 f(x)的图象关于(1，1)对称，即 f(x) f(2x)2，由 f(a) f(b)2，所以ab2，故选A． tanAtanB 4．因为 tanAtanBtanAtanB1，所以tanAtanB1tanAtanB，即 1tanAtanB 2 1tan(AB)tan(πC)tanC，所以 tanC 1，即cosC  ，故选B． 2 5．由等比数列前 n 项和的性质可得， S，S S，S S ，S S 成等比数列，则 5 10 5 15 10 20 15 S S S S S S x5 105x 10 5  15 10  20 15 ，设S x，则  ，∵等比数列{a }中，a 0， S S S S S 10 5 x5 n n 5 10 5 15 10 S 105 10525 ∴解得，x25，故S 25，∴ 20  S 425，故选D． 10 10525 255 20 1 1 1 1 1 1 6．对于 A：ln ln10，0sin 1，22 20 1，∴ln sin 22 ，A 错误；对于 B： 2 2 2 2 π 2 π 2 π 1sin1 sin  ，cos1cos  ，tan1tan 1，∴cos1sin1tan1，B 错误； 4 2 4 2 4 1 1 1 对 于 C： 8 7  ， 7 6  ， 6 5  ， ∵ 8 7  8 7 7 6 6 5 1 1 1 7 6  6 5 0，∴   ，即 8 7  7 6  6 5， 8 7 7 6 6 5 数学参考答案·第1页（共10页） {#{QQABLQaAggiIQIBAAAgCEwGqCgMQkAGAASgGgBAMIAAAiQFABCA=}#}lg2lg4 2 lg8 2 lg9 2 C 正确；对于 D，由于lg2lg4  ，所以lg2lg4    ，即  2   2   2  lg3 lg4 lg2lg4(lg3)2 ，所以  ，即 log 3log 4 ；同理， log 4log 5 ，所以 lg2 lg3 2 3 3 4 log 3log 4log 5，D错误，故选C． 2 3 4  π  π π π π π 7．由题意，函数f(x) 2sinx (0)，由于x  0，  ，所以x   ，   ；  4  2 4 4 2 4  π π 2π≤  ，  π   2 4 7 11 又 由 f(x) 在  0，  上 恰 有 两 个 根 ， 所 以  即 ≤ ； 令  2 3π π  π ， 2 2  2 4 π π 1 1 7 11 41 2π kπ (kZ)，则 k ，又0且 ≤ ，则  ，故选B． 4 2 2 8 2 2 max 8 x2 y2 x2 y2 8．设c2 a2 b2，则F(c，0)，F (c，0)；由点P(x，y )在C：  1上，则有 1  1 1， 1 2 1 1 a2 b2 a2 b2  x2   x2  c2x2 即y2 b2 1 1 ，所以|PF | (x c)2  y2  (x c)2 b2 1 1  1 2cx a2  1  a2  1 1 1 1  a2  a2 1 cx  2 cx 1 a ；又 a≤x≤a ，所以 |PF | 1 aex a，|PF |2a|PF |aex ，则    a  1 1 a 1 2 1 1 |PF ||PF |2ex ；如图 1，由焦点△PFF 的内切 1 2 1 1 2 圆可得：|PE||PF|，|EF ||FH |，|FF ||F H |，所 1 1 2 2 以 |PF ||PF ||EF ||FF ||FH ||F H |2ex ； 又 1 2 1 2 1 2 1 |FH ||F H |(cx )(cx ) 2ex 2x ， 所 以 1 2 2 2 1 2 图1 x 3 x ex ，即e 2  ，故选A． 2 1 x 2 1 二、多项选择题（本大题共3小题，每小题6分，共18分．在每小题给出的四个选项中，有 多项符合题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分） 题号 9 10 11 答案 AD ABD BCD 数学参考答案·第2页（共10页） {#{QQABLQaAggiIQIBAAAgCEwGqCgMQkAGAASgGgBAMIAAAiQFABCA=}#}【解析】 5 7 9 9．∵   0.7，∴该商店六月份鲜花饼日销售量的第70%分位数是550，A 正确； 30 30 30 53007400950046005700 六月份平均每天销售鲜花饼 490个，B错误； 30 4 5 3 根据销售数据得：日销售量大于550个的概率为   ，C错误；日销售量小于450 30 30 10 5 7 12 2 个的概率为    ，D正确，故选AD． 30 30 30 5 1 1 1 1  1  10．由a 2a a a 0，a 1，得： 2 0，  2，∴ 是公差 n1 n n1 n 1 a a a a a  n n1 n1 n n 1 1 为 2，首项为 1 的等差数列，故 1(n1)22n1，即a  ，C 错误；所以 a n 2n1 n 1 b 32n1   1   b 3an 32n1，b 32n1 n1  32 9，故3an 是等比数列，A 正确；对于 B： n n1 b 32n1 n   1 1 1 n(12n1) 2n1，c  (1352n1)  n，故数列{c }为等差数列，B a n n n 2 n n 1 1 1 1 (14n3)(2n1) 正确；对于D：    135(4n3)  a a a a 2 1 2 3 2n1 2n1 (2n1)2  ，D正确，故选ABD． a n 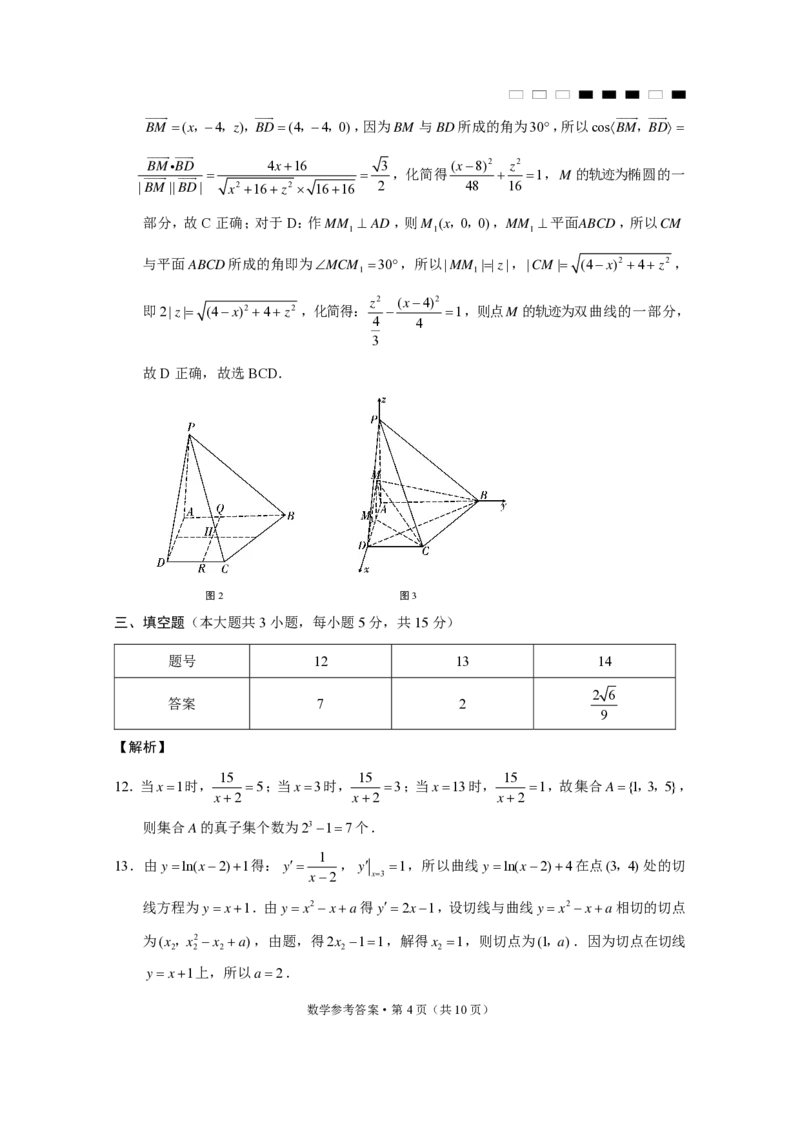11．对于A：如图2，过点H 作HRCD交CD于点R，则点H 到CD的距离为HR；过点H 作HQ AB交AB于点Q，由于PA平面ABCD，则HQPA，所以HQ平面PAB， 则点H 到平面PAB的距离为HQ；∵AB∥CD且点H 到CD的距离等于其到平面PAB的 距离，∴点H 在AD的垂直平分线上，故 A 错误；建立如图 3 所示的空间直角坐标系 Axyz：设M(x，0，z)，A(0，0，0)，B(0，4，0)，C(4，2，0)，D(4，0，0)，对于 B： ∵ BADA ， BAPA ，∴BA平面PDA ，即 BAMA ，同理： CDMD ，又 MA AB x2 z2 ∵BMACMD， ∴△BAM~△CDM ，∴  2，即 2，化简 MD DC (x4)2 z2  16 2 8 2 得 x  z2   ，即点 M 的轨迹为圆的一部分，故 B 正确；对于 C，  3  3 数学参考答案·第3页（共10页） {#{QQABLQaAggiIQIBAAAgCEwGqCgMQkAGAASgGgBAMIAAAiQFABCA=}#}    BM (x，4，z)，BD(4，4，0)，因为BM 与BD所成的角为30，所以cosBM，BD   BMBD 4x16 3 (x8)2 z2     ，化简得  1，M 的轨迹为椭圆的一 |BM ||BD| x2 16z2  1616 2 48 16 部分，故 C正确；对于D：作MM  AD，则M (x，0，0)，MM 平面ABCD，所以CM 1 1 1 与平面ABCD所成的角即为MCM 30，所以|MM ||z|，|CM | (4x)2 4z2 ， 1 1 z2 (x4)2 即2|z| (4x)2 4z2 ，化简得：  1，则点M 的轨迹为双曲线的一部分， 4 4 3 故D正确，故选BCD． 图2 图3 三、填空题（本大题共3小题，每小题5分，共15分） 题号 12 13 14 2 6 答案 7 2 9 【解析】 15 15 15 12．当x1时， 5；当x3时， 3；当x13时， 1，故集合A{1，3，5}， x2 x2 x2 则集合A的真子集个数为23 17个． 1 13．由yln(x2)1得： y ，y 1，所以曲线yln(x2)4在点(3，4)处的切 x2 x3 线方程为yx1．由yx2 xa得y2x1，设切线与曲线yx2 xa相切的切点 为(x，x2 x a)，由题，得2x 11，解得x 1，则切点为(1，a)．因为切点在切线 2 2 2 2 2 yx1上，所以a2． 数学参考答案·第4页（共10页） {#{QQABLQaAggiIQIBAAAgCEwGqCgMQkAGAASgGgBAMIAAAiQFABCA=}#}14．由正弦定理，bab2 a3 a，则有(ab)(1a2 ab)0，由于ab，所以a2 ab1c2， 由余弦定理得，a2 aba2 b2 2abcosC，则a2acosC b ，又由正弦定理，得 sinA2sinAcosC sinBsin(AC)，即sinAsin(CA)，则有CA A，即C 2A．因 π  3 为 C 2A ，所以 BπAC π 3A0 ，故 0 A ，则 sinA0，  ； 3  2    sinBsinA sin(AC) sinAsin3A sinAsin2AcosA cos2AsinAsinA  3 2sinAcos2A(12sin2A)sinAsinA 4sin3 A 2sinA ； 设 xsinA0，  ，   2   6 6 f(x)4x3 2x，则 f(x)12x2 2，令 f(x)0得x 或者x （舍），且当 6 6 6 6  6 0x 时， f(x)0，当x 时， f(x)0，则 f(x)在0， 上单调递增，在   6 6 6    6 3 6  ，  上单调递减，故当 x 时， f(x) 取最大值，故sinBsinA 最大值为   6 2 6    6 2 6 f   ．   6 9   四、解答题（本大题共5小题，共77分．解答应写出文字说明，证明过程或演算步骤） 15．（本小题满分13分） 解：（1）由于r0.96，由题可知利润y与投资金额x相关性较强． …………………………………………（1分） n (x x)(y  y) i i i1 n n (x x)2 (y  y)2 b ˆ i i 1 n 1 n 又  i1  i1 ，S2  (y  y)2 ，S2  (x x)2 ， r n n y n i x n i (x x)(y  y) (x x)2 i1 i1 i i i i1 i1 n n (x x)2 (y  y)2 i i i1 i1 b ˆ nS2 S 所以  y  y ； …………………………（3分） r nS2 S x x 数学参考答案·第5页（共10页） {#{QQABLQaAggiIQIBAAAgCEwGqCgMQkAGAASgGgBAMIAAAiQFABCA=}#}S 3.6 又S2 12，S2 3.6，所以b ˆ  y r 0.96 300.0960.53， x y S 12 x …………………………………（6分） 1 10 1 10 由题，得x  x 7，y  y 4， 10 i 10 i i1 i1 所以a   yb  x470.530.29， 则y关于x的经验回归方程为yˆ 0.53x0.29． …………………………（8分） （2）由题意知，该地区150名使用A型充电桩车主，男车主有90名，女性车主有60名 对A型充电桩的使用表示满意的男性车主有60名，对A型充电桩的使用表示满意的女 性车主有36名． 设该地区“一位车主对A型充电桩的使用表示满意”记作事件A，“车主是男性”记作 事件B，该地区一位车主对A型充电桩的使用表示满意，这位车主是男性的概率为： 60 P(AB) 150 5 P(B|A)   ． …………………………（13分） P(A) 60 36 8  150 150 16．（本小题满分15分） 解：（1）设等比数列{a }的公比为q，且有q1， n a2q6 64， a 1， 由于 1 解得 1 aq2 aq4 20， q2， 1 1 所以数列{a }的通项公式为a 2n1． …………………………（4分） n n 由于{b }是等差数列，设b  AnB， n n 则有(n1)b (n1)(AnB) An2 (AB)nB2n2 nC， n A2， A2，   所以AB1，解得B1，   BC， C 1， 所以数列{b }的通项公式为b 2n1． …………………………（8分） n n 1 1 1 1  （2）由（1）知，c (2)n1 (2)n1    ， n (2n1)(2n1) 22n1 2n1 …………………………（10分） 数学参考答案·第6页（共10页） {#{QQABLQaAggiIQIBAAAgCEwGqCgMQkAGAASgGgBAMIAAAiQFABCA=}#}1 1 1 1  1 1  所以S n [(2)0 (2)1(2)n1] 2     1 3    3  5    2n1  2n1     1(2)n 1 1  1(2)n1 1   1    ． …………………………（15分） 12 2 2n1 6 4n2 17．（本小题满分15分） （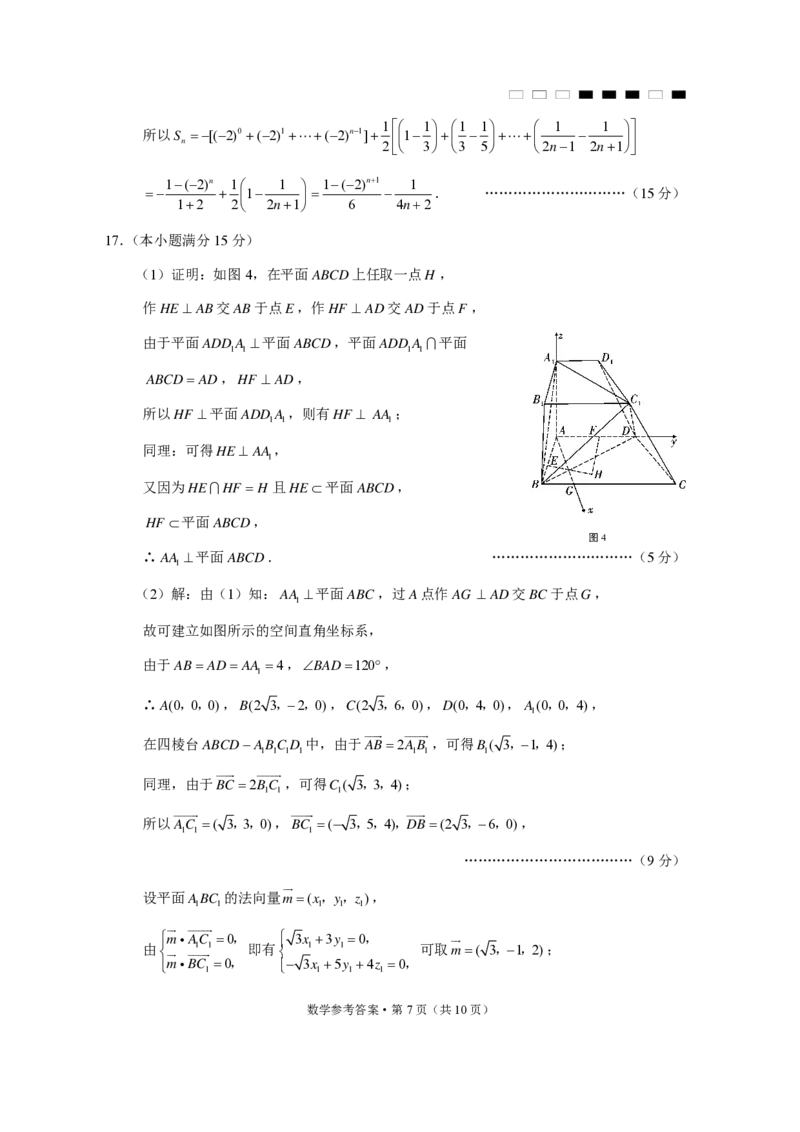1）证明：如图4，在平面ABCD上任取一点H ， 作HE AB交AB于点E，作HF  AD交AD于点F ， 由于平面ADDA 平面ABCD，平面ADDA 平面 1 1 1 1 ABCD AD，HF  AD， 所以HF 平面ADD A ，则有HF  AA ； 1 1 1 同理：可得HE AA， 1 又因为HEHF H 且HE平面ABCD， HF 平面ABCD， 图4 ∴AA 平面ABCD． …………………………（5分） 1 （2）解：由（1）知：AA 平面ABC，过A点作AG  AD交BC于点G， 1 故可建立如图所示的空间直角坐标系， 由于AB AD AA 4，BAD120， 1 ∴A(0，0，0)，B(2 3，2，0)，C(2 3，6，0)，D(0，4，0)，A(0，0，4)， 1   在四棱台ABCDABCD 中，由于AB2AB ，可得B( 3，1，4)； 1 1 1 1 1 1 1   同理，由于BC 2BC ，可得C ( 3，3，4)； 1 1 1    所以AC ( 3，3，0)，BC ( 3，5，4)，DB(2 3，6，0)， 1 1 1 ………………………………（9分）  设平面ABC 的法向量m(x，y，z )， 1 1 1 1 1    m AC 0，   3x 3y 0，  由 11 即有 1 1 可取m( 3，1，2)； mBC 0，  3x 5y 4z 0， 1 1 1 1 数学参考答案·第7页（共10页） {#{QQABLQaAggiIQIBAAAgCEwGqCgMQkAGAASgGgBAMIAAAiQFABCA=}#} 设平面DBC 的法向量n(x，y，z )， 1 2 2 2    nDB0，  2 3x 6y 0，  由  即有 2 2 可取n(2 3，2，1)； nBC 0，  3x 5y 4z 0， 1 2 2 2     |mn| 2 34 所以|cosm，n|     ， |m||n| 8 17 34 34 ∴平面ABC 与平面DBC 夹角的余弦值为 ． ………………………（15分） 1 1 1 34 18．（本小题满分17分） 解：（1）设c2 a2 b2，由题，焦距为4，故c2， …………………………（1分） 当|AB|6时，可得A(2，3)． 4 9 把A(2，3)代入C中得，  1①， a2 b2 又a2 b2 4②， 则联立①②方程得，a2 1，b2 3． y2 所以C的方程为x2  1． …………………………（5分） 3 （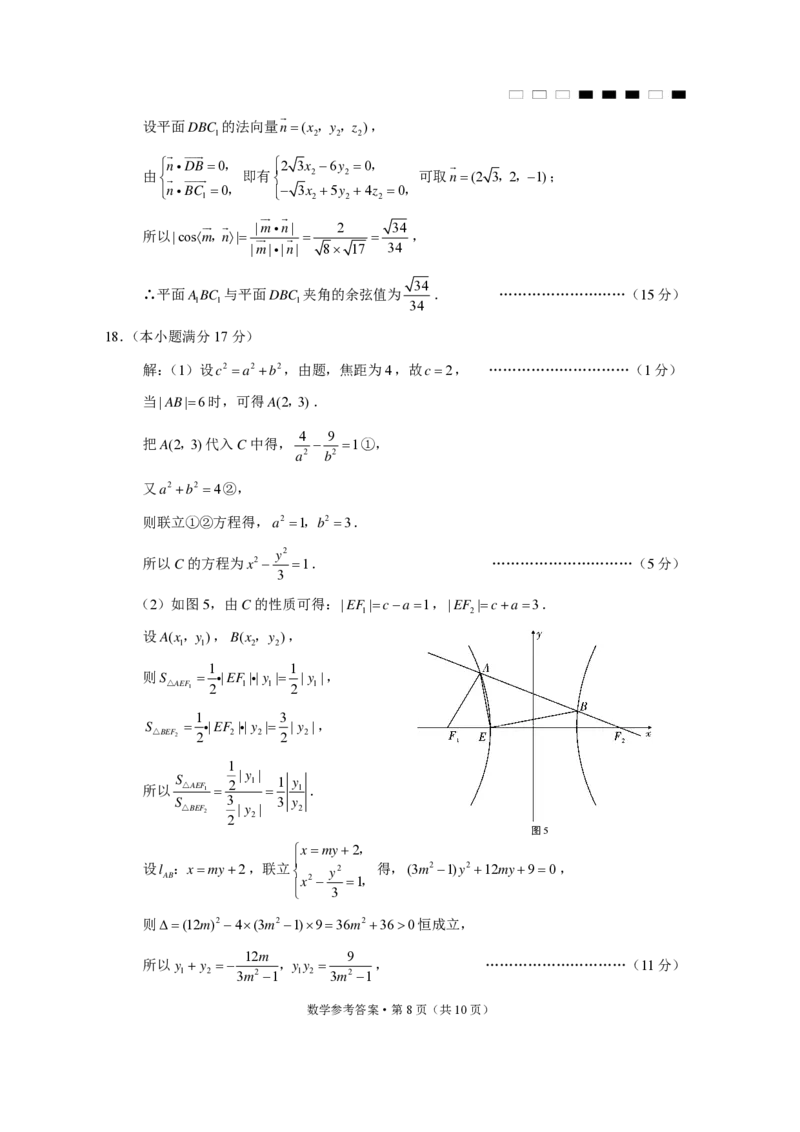2）如图5，由C的性质可得：|EF |ca1，|EF |ca3． 1 2 设A(x，y )，B(x，y )， 1 1 2 2 1 1 则S  |EF || y | | y |， △AEF1 2 1 1 2 1 1 3 S  |EF || y | | y |， △BEF2 2 2 2 2 2 1 | y | 所以 S △AEF1  2 1  1 y 1 ． S 3 3 y △BEF2 2 | y 2 | 2 图5 xmy2，  设l ：xmy2，联立 y2 得，(3m2 1)y2 12my90， AB x2  1，  3 则(12m)2 4(3m2 1)936m2 360恒成立， 12m 9 所以y  y  ，y y  ， …………………………（11分） 1 2 3m2 1 1 2 3m2 1 数学参考答案·第8页（共10页） {#{QQABLQaAggiIQIBAAAgCEwGqCgMQkAGAASgGgBAMIAAAiQFABCA=}#}由于l与C交于异支，则y y 0， 1 2 1 解得：m2  ； 3  12m  2 16 16 16   (3m2 1) (y  y )2  3m2 1 16m2 3 3 16 3 16 又 1 2       ， y y 9 3m2 1 3m2 1 3 3m2 1 3 1 2 3m2 1 (y  y )2 y2  y2 2y y y y 且 1 2  1 2 1 2  1  2 2． y y y y y y 1 2 1 2 2 1 y 1 16 1 令t  1 ，且t0，则t 2 ，解得：0t 或t 3， y t 3 3 2 S 1 y 1  1 则 △AEF1  1  t0，  (1，)， S 3 y 3  9 △BEF2 2 S  1 所以 △AEF1 的取值范围为 0，  (1，)． …………………………（17分） S  9 △BEF2 19．（本小题满分17分） 解：（1）g(x)2xsinx，xR； 令 p(x)2xsinx，则有 p(x)2cosx0，所以 p(x)g(x)在R上单调递增． 又g(0)0，所以当x0时，g(x)0，g(x)在(，0)上单调递减； 当x0时，g(x)0，g(x)在(0，)上单调递增， 所以g(x)x2 cosx不是山峰函数． …………………………（5分） （2）由题意可知：函数h(x)(m2)xx2 mx在区间[0，1]上先增后减，且存在峰点． 由于h(x)m22xmx lnm， 又当m1时，lnm0，则h(x)在[0，1]上单调递减， h(0)m2lnm0， 所以 h(1)mmlnm0， 1 设q(m)m2lnm，m1，所以q(m)1 0，则q(m)在(1，)上单调递增. m 所以当m1时，q(m)q(1)30，即此时m2lnm0恒成立； 由于当m1时，不等式mmlnm0等价于lnm1，即me， 故m的取值范围是(e，)． …………………………（10分） 数学参考答案·第9页（共10页） {#{QQABLQaAggiIQIBAAAgCEwGqCgMQkAGAASgGgBAMIAAAiQFABCA=}#}（3）由题意得：I(x)(3x2 4nx4n4)lnxx2 2nx(4n4)x2 2nx(4n4) (3x2 4nx4n4)lnx． 若3x2 4nx4n4≥0恒成立，则函数yI(x)在(0，1)上单调递减，在(1，)单调递增， 不是山峰函数，不符合题意； 因此关于x的方程3x2 4nx4n40有两个相异实根，设两根为，且， 且有16n2 48(n1)0； 2 2 由于当x0时，I(x)0，且I 0，I  ≤I(1)， 3 3 所以函数yI(x)在(0，1)上不单调； 3 同理，由于当x时，I(x)，且I  ≤I(1)， 2 所以yI(x)在(1，)上不单调，从而有01，1. 因此yI(x)在(0，)和(1，)上单调递减，在(，1)和(，)上单调递增； 从而函数yI(x)的峰值区间为[s，t]，必满足[s，t][，]．  4 所以d(n)  n2 3n3． 3 3 2 16(3n4) 2 4(45n52) 11 由于I  ln  ，I(1)3n ， 3 27 3 81 3 3 3(4n7) 3 30n39 I  ln  ， 2 8 2 8 16(3n4) 2 4(45n52) ln  0，  27 3 81  16(3n4) 2 4(45n52) 11 由题意知n满足不等式组： ln  ≤3n ， 27 3 81 3   3(4n7) 3 30n39 11 ln  ≤3n .   8 2 8 3 3 3 2 由于当n 时，满足上述不等式组，则有d(n) d  3， 2 min 2 3 2 3 即d(n)的最小值为 ． …………………………（17分） 3 数学参考答案·第10页（共10页） {#{QQABLQaAggiIQIBAAAgCEwGqCgMQkAGAASgGgBAMIAAAiQFABCA=}#}