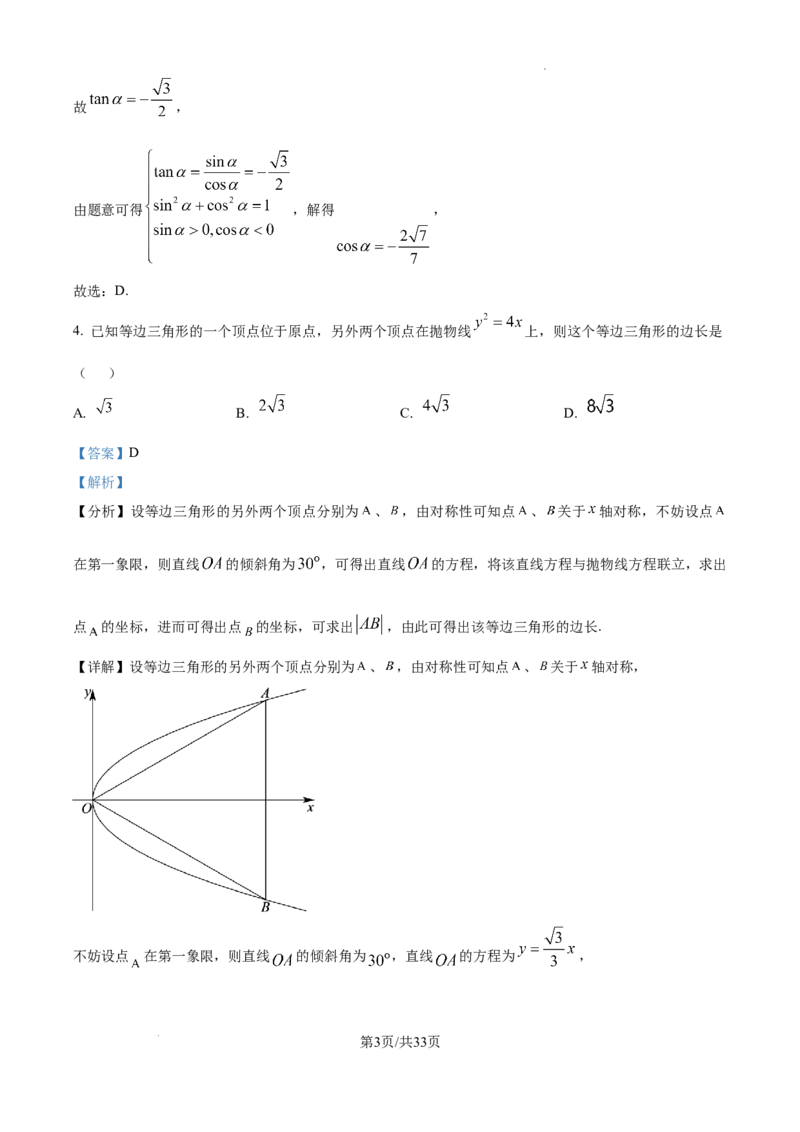文档内容
2026 年东北三省一区八校联合体第一次模拟考试
数学科试卷
注意事项:
1.答卷前,考生务必将自己的考生号、姓名、考点学校、考场号及座位号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需要
改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写
在本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题:(本题共 8小题,每小题5分,共40分,在.每小题给出的四个选项中,只有
一项是符合题目要求的)
1. 已知复数 、 、 满足 , , ,则复数 在复平面对应的点在(
)
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
【答案】A
【解析】
【分析】利用复数的四则运算化简复数 ,利用复数的几何意义可得出结论.
【详解】由题意可得
,
故 ,
所以,复数 在复平面内对应点的坐标为 ,位于第一象限.
故选:A.
2. 已知非零实数 不全相等,给出下面两个命题.命题p:若 成等差数列,则 也成等差
第1页/共33页
学科网(北京)股份有限公司数列;命题q∶ 若 成等比数列,则 也成等比数列,则( )
A. 命题p和q均为真命题 B. 命题p和命题 均为真命题
C. 命题 和命题q均为真命题 D. 命题 和命题 均为真命题
【答案】C
【解析】
【分析】对于命题 ,举例可说明其为假命题;对于命题 ,根据等比中项可推导.
【详解】对于命题 :易得1,2,3成等差, 不成等差,故命题 为假命题;
对于命题 : 成等比数列,则 ,所以 ,
即 成等比数列,故命题 为真命题.
综上,命题 为假命题, 为真命题,命题 为真命题, 为假命题.
故选:C.
3. 已知 是钝角, ,则 ( )
A. B. C. D.
【答案】D
【解析】
【分析】由同角三角函数的基本关系可得出 的值,利用同角三角函数的基本关系可得出关于 、
的方程组,结合 是钝角可求得 的值.
【详解】因为 为钝角,则 , ,
所以
,
第2页/共33页
学科网(北京)股份有限公司故 ,
由题意可得 ,解得 ,
故选:D.
4. 已知等边三角形的一个顶点位于原点,另外两个顶点在抛物线 上,则这个等边三角形的边长是
( )
A. B. C. D.
【答案】D
【解析】
【分析】设等边三角形的另外两个顶点分别为 、 ,由对称性可知点 、 关于 轴对称,不妨设点
在第一象限,则直线 的倾斜角为 ,可得出直线 的方程,将该直线方程与抛物线方程联立,求出
点 的坐标,进而可得出点 的坐标,可求出 ,由此可得出该等边三角形的边长.
【详解】设等边三角形的另外两个顶点分别为 、 ,由对称性可知点 、 关于 轴对称,
不妨设点 在第一象限,则直线 的倾斜角为 ,直线 的方程为 ,
第3页/共33页
学科网(北京)股份有限公司联立 可得 ,解得 或 ,即点 ,
故点 ,则 ,
因此,该等边三角形的边长为 .
故选:D.
5. 已知 、 ,则 的最小值是(
)
A. B. C. D.
【答案】C
【解析】
【 分 析 】 记 点 、 、 、 , , 可 得 出
,数形结合可
得出所求代数式的最小值.
【详解】记点 、 、 、 , ,如下图所示:
易知四边形 是边长为 的正方形,
所以 , , , ,
所以 ,
第4页/共33页
学科网(北京)股份有限公司在
当且仅当点 线段 上时,等号成立,
,
当且仅当点 在线段 上时,等号成立,
所以
,
当且仅当点 为线段 、 的交点时,等号成立,
故 的最小值为 .
故选:C.
6. 用半径为 的圆形铁皮剪出一个圆心角为 的扇形,制成一个圆锥形容器,则该圆锥形容器的容积最大
值是( )
A. B. C. D.
【答案】B
【解析】
【分析】先利用扇形弧长与圆锥底面周长相等得出 ,再利用体积公式求出体积 ,其是关于 的
函数,通过构造函数 ,其中 ,研究最大值,求出 ,即可求出 的最大值.
【详解】设圆形半径为 ,圆锥底面半径为 ,
则扇形的弧长为 ,圆锥底面周长为 ,则 ,即 ,
则圆锥的高为 ,
则圆锥的体积为
设 ,其中 ,则 ,
第5页/共33页
学科网(北京)股份有限公司由 得 ; 得 ,
则 在 上单调递增,在 上单调递减,
故当 时, 取最大值,即 时,圆锥的体积 取最大值,
且 ,
故选:B.
7. 7名教师甲、乙、丙、丁、戊、己、庚带领学生参加“探秘未知”活动,教师随机分为4组,每组至少
一人,则甲乙同组且丙丁同组的概率为( )
A. B. C. D.
【答案】A
【解析】
【分析】由题知不同的分组方法有4,1,1,1;3,2,1,1;2,2,2,1三种;利用不平均分组问题计算方法数,列出
符合题意得情况,然后求概率即可.
【详解】根据题意,不同的分组方法有4,1,1,1;3,2,1,1;2,2,2,1三种;
当分组为4,1,1,1时,共有 种,其中甲乙同组且丙丁同组有1种;
当分组 3,2,1,1时,共有 种,其中甲乙同组且丙丁同组有 种;
为
当分组为2,2,2,1时,共有 种,其中甲乙同组且丙丁同组有 种;
所以乙同组且丙丁同组的概率为 .
故选:A.
8. 已知 ,其中c>0,则当 最小时,c的值为( )
第6页/共33页
学科网(北京)股份有限公司A. B. C. D.
【答案】B
【解析】
【分析】由导数得 ,当且仅当 时等号成立, ,当
且仅当 时,等号成立;由向量模的计算及基本不等式得,
,即可求解.
【详解】由 ,
令 ,令 ,解得 ,
当 时, ,则 在 单调递增,
当 时, ,则 在 单调递减,
所以 ,
所以 ,当且仅当 时等号成立;
令 ,则 ,
令 ,则
,
第7页/共33页
学科网(北京)股份有限公司所以 在 上单调递增,
因为 ,所以当 时, ,即 ,
所以 在 上单调递减;
当 时, ,即 ,
所以 在 上单调递增;
所以 ,
因为 ,
所以
,
当且仅当 (*), 时等号成立,
由 得, ,
将 , , 代入(*)得, ,
所以 ,
故选:B.
二、选择题:(本题共3小题,每小题6分,共18分,在每小题给出的选项中,有多项符合
题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.)
9. 建筑学规定,民用住宅的窗户面积必须小于地板面积.但按采光标准,窗户面积与地板面积的比值不小
第8页/共33页
学科网(北京)股份有限公司于 ,并且这个比值越大,住宅的采光条件越好.现欲在原设计方案的基础上,同时增加住宅的窗户面
积和地板面积,则下列有关说法正确的是( )
的
A. 若增加 窗户面积和地板面积相同,则住宅的采光条件一定变好
B. 若增加的窗户面积和地板面积相同,则住宅的采光条件一定变差
C. 若增加的窗户面积和地板面积比值为 ,则住宅的采光条件一定变差
D. 若增加的窗户面积和地板面积比值为 ,则住宅的采光条件一定变差
【答案】AD
【解析】
【分析】设窗户面积与地板面积分别为 、 ,由题意可知 ,即 ,结合作差法逐项判
断即可.
【详解】设窗户面积与地板面积分别为 、 ,由题意可知 ,即 ,
按采光标准,窗户面积与地板面积的比值 ,且当 越大时,住宅的采光条件越好.
对于AB选项,当 时, ,
故 ,所以若增加的窗户面积和地板面积相同,则住宅的采光条件一定变好,A对B错;
对于C选项,若增加的窗户面积为 ,则增加的地面面积为 ,
故 ,
若 ,则 ,此时住宅的采光条件不变,C错;
第9页/共33页
学科网(北京)股份有限公司对于D选项,若增加的窗户面积为 ,则增加的地面面积为 ,
故 ,
所以若增加的窗户面积和地板面积比值为 ,则住宅的采光条件一定变差,D对.
故选:AD.
的
10. 在斜三角形 中,下列结论可能成立 是( )
A. B.
C. D.
【答案】BD
【解析】
【分析】利用正弦定理结合三角形三边关系可判断A选项;利用两角和的正切公式可判断B选项;利用三
角恒等变换结合正切函数的单调性可判断C选项;取 ,结合二倍角的正弦公式求出 的值,可
判断D选项.
【详解】在斜三角形 中,设内角 、 、 的对边分别为 、 、 ,
对于A选项,若 ,由正弦定理可得 ,
由三角形三边关系可知等式 不成立,A错;
对于B选项,若 ,
由两角和的正切公式可得 ,
故 ,
因为 ,故只需 即可,合乎题意;
第10页/共33页
学科网(北京)股份有限公司对于C选项,若 ,则 ,
即 ,
所以 ,即 ,
因为 、 ,故 , ,
所以 ,
即 ,
即 ,
因为 、 ,则 、 ,故 ,
所以 ,
由题意可得 ,故 ,
由于 ,故 ,
因为正切函数 在 上单调递增,故 ,整理得 ,
这与三角形的内角和定理矛盾,C错;
第11页/共33页
学科网(北京)股份有限公司对于D选项,若 ,由 可得 ,
即 ,
等式两边平方可得 ,
即 ,因为 ,解得 ,
因为 ,则 ,故 ,则 ,
由于 , ,
所以满足条件 的锐角 存在,D对.
故选:BD.
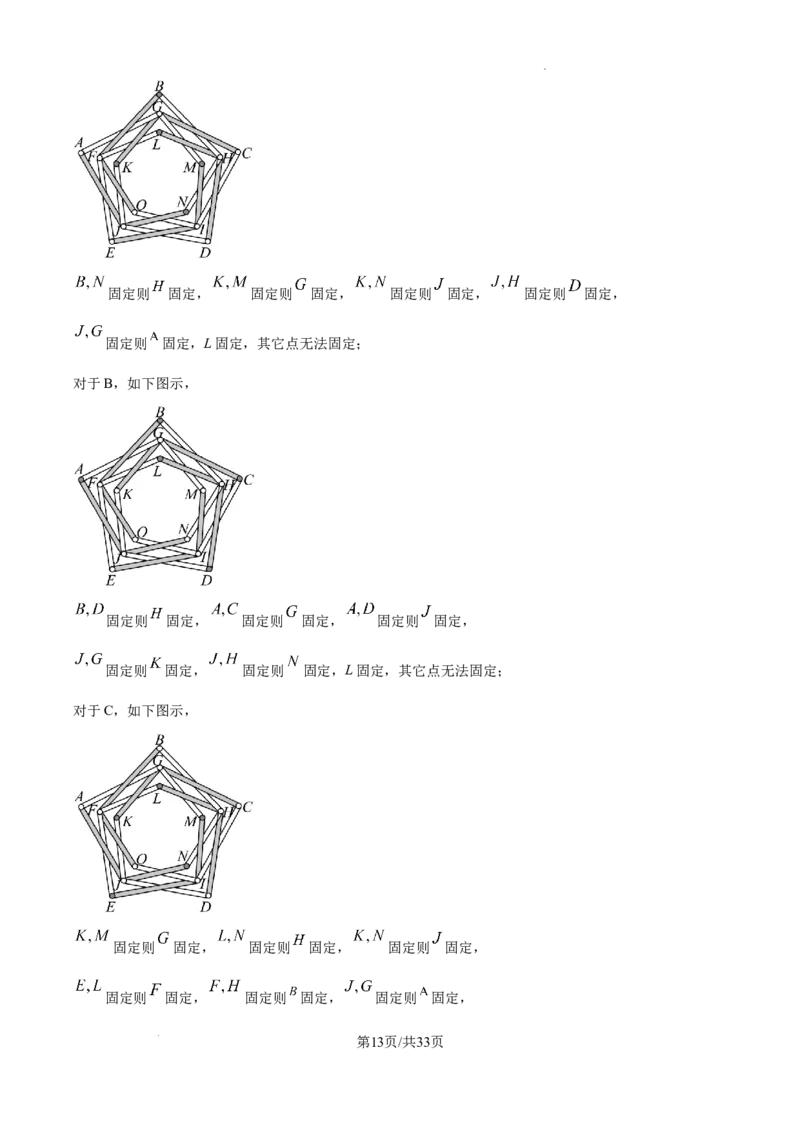
11. 下面的图形由铰接的薄片构成,固定某一些点会导致所有两杆固定,则下列选项说法正确的是( )
A. 若固定 ,则所有连杆固定 B. 若固定 ,则所有连杆固定
C. 若固定 ,则所有连杆固定 D. 若固定 ,则所有连杆固定
【答案】CD
【解析】
【分析】利用三角形的稳定性,结合各项对应的固定点判断连杆是否固定即可.
【详解】对于A,如下图示,
第12页/共33页
学科网(北京)股份有限公司固定则 固定, 固定则 固定, 固定则 固定, 固定则 固定,
固定则 固定,L固定,其它点无法固定;
对于B,如下图示,
固定则 固定, 固定则 固定, 固定则 固定,
固定则 固定, 固定则 固定,L固定,其它点无法固定;
对于C,如下图示,
固定则 固定, 固定则 固定, 固定则 固定,
固定则 固定, 固定则 固定, 固定则 固定,
第13页/共33页
学科网(北京)股份有限公司固定则 固定, 固定则 固定, 固定则 固定,
固定则 固定,所有连杆会固定;
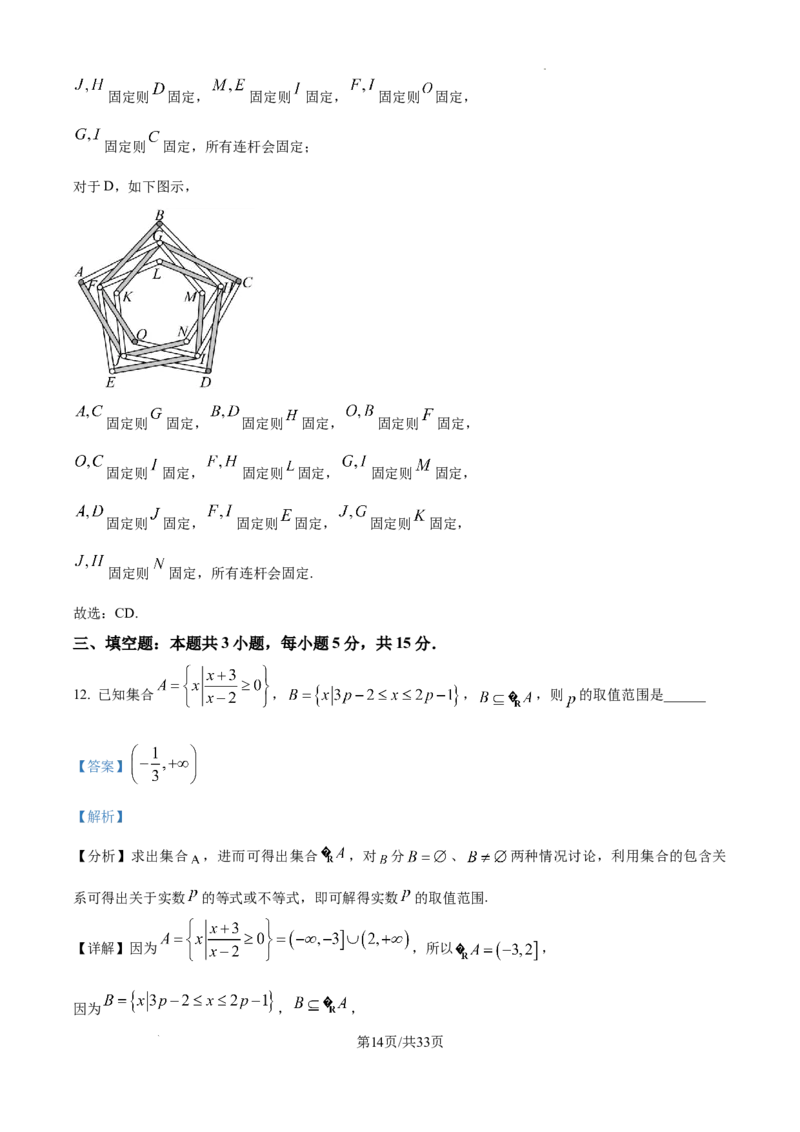
对于D,如下图示,
固定则 固定, 固定则 固定, 固定则 固定,
固定则 固定, 固定则 固定, 固定则 固定,
固定则 固定, 固定则 固定, 固定则 固定,
固定则 固定,所有连杆会固定.
故选:CD.
三、填空题:本题共3小题,每小题5分,共15分.
12. 已知集合 , , ,则 的取值范围是______
【答案】
【解析】
【分析】求出集合 ,进而可得出集合 ,对 分 、 两种情况讨论,利用集合的包含关
系可得出关于实数 的等式或不等式,即可解得实数 的取值范围.
【详解】因为 ,所以 ,
因为 , ,
第14页/共33页
学科网(北京)股份有限公司当 时, ,即 ,合乎题意;
当 时,由于 ,所以有 ,解得 .
综上所述,实数 的取值范围是 .
故答案为: .
13. 函数 过原点的切线方程为________.
【答案】 或
【解析】
【分析】设切点坐标为 ,利用导数的几何意义可得出关于 的等式,解出 的值,即可得出所
求切线的方程.
【详解】设切点为 ,对函数 求导得 ,切线斜率为 ,
由于切线过原点,则 ,整理得 ,即 ,
解得 ,
当 时,切线斜率为 ,此时切线方程为 ;
当 时,切线斜率为 ,此时切线方程为 .
故答案为: 或 .
第15页/共33页
学科网(北京)股份有限公司14. 设正整数数列 满足 ,则 的前 项中偶数的个
数是_______.
【答案】
【解析】
【分析】分别令 、 、 ,求出数列 前 项的值,猜想得出 ,
再利用数学归纳法证明出猜想成立,然后列举出数列 前若干项的值,可知 ,即可得解.
【详解】当 时,由题意可得 ,
因为数列 是正整数数列,假设 ,则 ,
为了满足 为正,只需 ,即 ,
假设 ,则 ,可得 ,合乎题意,
假设 ,则 ,可得 不是正整数,
故 ,从而可得 ,
当 时,则有 ,即 ,解得 ,
当 时, ,
即 ,解得 ,
第16页/共33页
学科网(北京)股份有限公司当 时, ,
猜想 ,
假设当 时,猜想成立,即 ,
当 时, ,
由猜想可得 ,则 ,
所以
,
所以
,
这说明当 时猜想也成立,故数列 满足 ,
所以,数列 的各项依次为: , , , , , , , , , , ,
由上可知 均为偶数,
又因为 ,故 的前 项中偶数的个数是 .
故答案为: .
四、解答题:本题共5小题,共77分,解答应写出文字说明、证明过程或演算步骤.
第17页/共33页
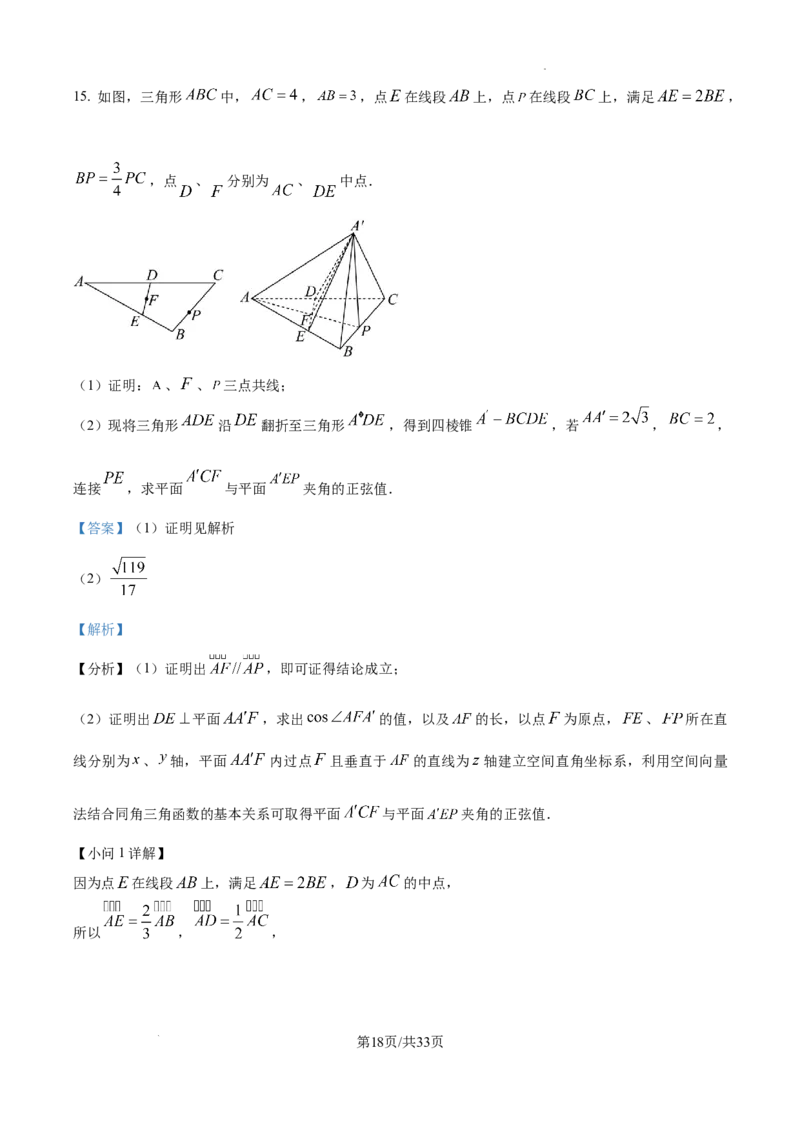
学科网(北京)股份有限公司15. 如图,三角形 中, , ,点 在线段 上,点 在线段 上,满足 ,
,点 、 分别为 、 中点.
(1)证明: 、 、 三点共线;
(2)现将三角形 沿 翻折至三角形 ,得到四棱锥 ,若 , ,
连接 ,求平面 与平面 夹角的正弦值.
【答案】(1)证明见解析
(2)
【解析】
【分析】(1)证明出 ,即可证得结论成立;
(2)证明出 平面 ,求出 的值,以及 的长,以点 为原点, 、 所在直
线分别为 、 轴,平面 内过点 且垂直于 的直线为 轴建立空间直角坐标系,利用空间向量
法结合同角三角函数的基本关系可取得平面 与平面 夹角的正弦值.
【小问1详解】
因为点 在线段 上,满足 , 为 的中点,
所以 , ,
第18页/共33页
学科网(北京)股份有限公司因为 为 的中点,所以 ,
因为点 在线段 上, ,即 ,
即 ,故 ,所以 ,
.
所以 、 、 三点共线
【小问2详解】
因为 , , , ,故 , ,
因为 为 的中点,所以 ,
将三角形 沿 翻折至三角形 ,得到四棱锥 ,则 ,
因为 , 、 平面 ,故 平面 ,
在 中, , , ,
由余弦定理可得 ,
在 中, ,
由余弦定理可得 ,
所以 ,故 ,
因为 ,故 ,
以点 为原点, 、 所在直线分别为 、 轴,平面 内过点 且垂直于 的直线为 轴建
立如图所示的空间直角坐标系,
第19页/共33页
学科网(北京)股份有限公司则 、 、 、 、 、
、 、 ,
设平面 的一个法向量为 , , ,
则 ,取 ,可得 ,
设平面 的一个法向量为 , , ,
则 ,取 ,可得 ,
所以 ,
故 .
因此,平面 与平面 夹角的正弦值为 .
16. 在斜三角形 中, .
第20页/共33页
学科网(北京)股份有限公司(1)设 为三角形 的内心,当 时,求 的最小值;
(2)是否存在函数 ,使得对于一切满足条件的 ,代数式 恒为定值?若存
在,请给出一个满足条件的 ,并证明之;若不存在,请给出理由.
【答案】(1)答案解析悬赏征集中,欢迎大牛老师们踊跃投稿! 答案解析悬赏征集中,欢迎大牛老师们踊跃
投稿!
(2)答案解析悬赏征集中,欢迎大牛老师们踊跃投稿! 答案解析悬赏征集中,欢迎大牛老师们踊跃投稿!
【解析】
【分析】略
【小问1详解】
在斜三角形 中, ,
所以 ,
当 时,则 ,
即 ,即 ,
延长 交 于点 ,设内切圆 切 、 边分别于点 、 ,如下图所示:
第21页/共33页
学科网(北京)股份有限公司则 ,在 中,由正弦定理得 ,故 ,
因为 为 的内心,则 平分 ,
故 ,即 ,故 ,则 ,即 ,
设内切圆 的半径为 ,
由等面积法可得 ,故 ,
所以 ,故
,
在 中,由正弦定理 ,得 ,
因为 ,则 ,
所以 ,
故 ,
【小问2详解】
答案解析悬赏征集中,欢迎大牛老师们踊跃投稿!联系人QQ:2853279698.
第22页/共33页
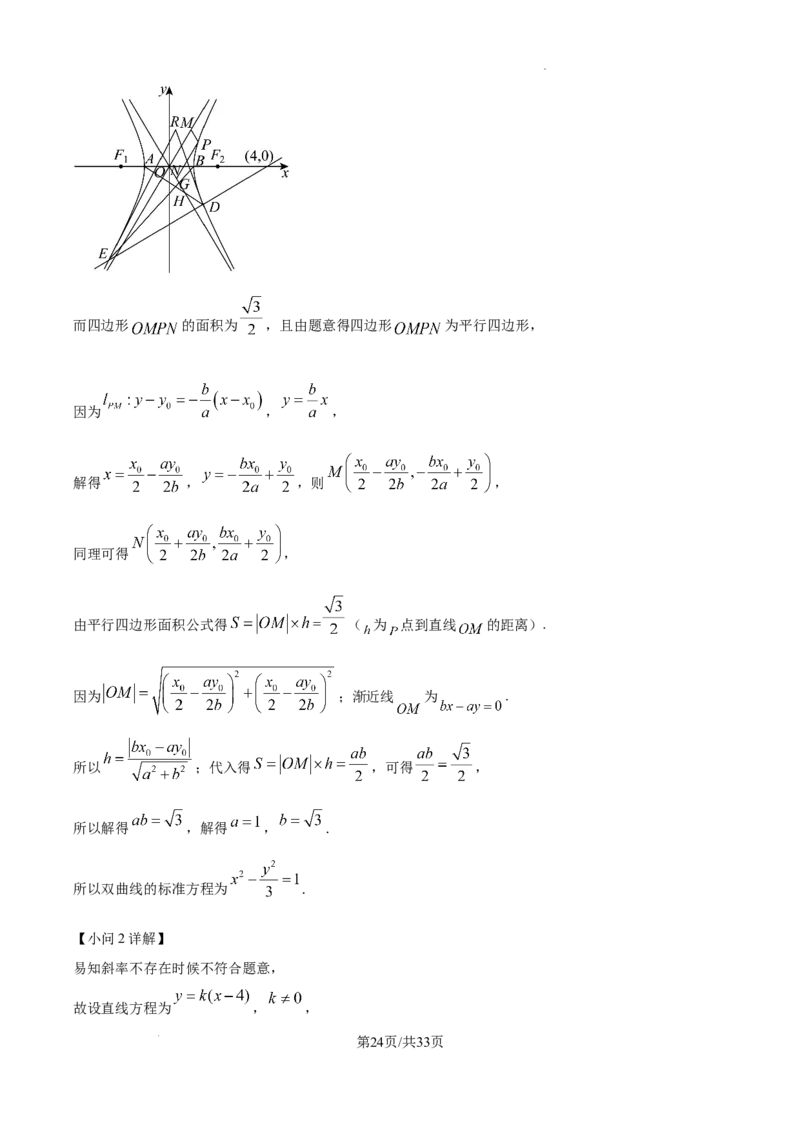
学科网(北京)股份有限公司17. 已知双曲线 的焦距为4,左右焦点分别为 ,若点P为双曲线C上一点,
过点P分别作双曲线C两条渐近线的平行线 ,与两条渐近线分别交于点 ,四边形
的面积为 .设点 分别为双曲线 的左右顶点,过点 的直线与双曲线 交于点 (不同
于点 .设直线 与 交于点G,直线 与 交于点H,双曲线在点 处的切线交于点R.
(1)求双曲线C的标准方程;
(2)试探究 是否是定值,若是,求出此定值;若不是,说明理由.
【答案】(1) .
(2) .
【解析】
【分析】(1)设出 点坐标 ,联立可解出 两点坐标,结合四边形 的面积为 建
立方程求出基本量,最后求出双曲线方程即可.
(2)联立方程组,利用韦达定理,求出关键点的坐标,再结合中点坐标公式进行化简证明即可.
【小问1详解】
已知双曲线 焦距为4,即 ,故 .
又因为 ,所以 .
如图,设点 在双曲线上,满足 ,双曲线的渐近线方程为 .
第23页/共33页
学科网(北京)股份有限公司而四边形 的面积为 ,且由题意得四边形 为平行四边形,
因为 , ,
解得 , ,则 ,
同理可得 ,
由平行四边形面积公式得 = ( 为 点到直线 的距离).
因为 ;渐近线 为 .
所以 ;代入得 ,可得 ,
所以解得 ,解得 , .
所以双曲线的标准方程为 .
【小问2详解】
易知斜率不存在时候不符合题意,
故设直线方程为 , ,
第24页/共33页
学科网(北京)股份有限公司代入双曲线方程联立可得 ,
化简得 .
且 ;
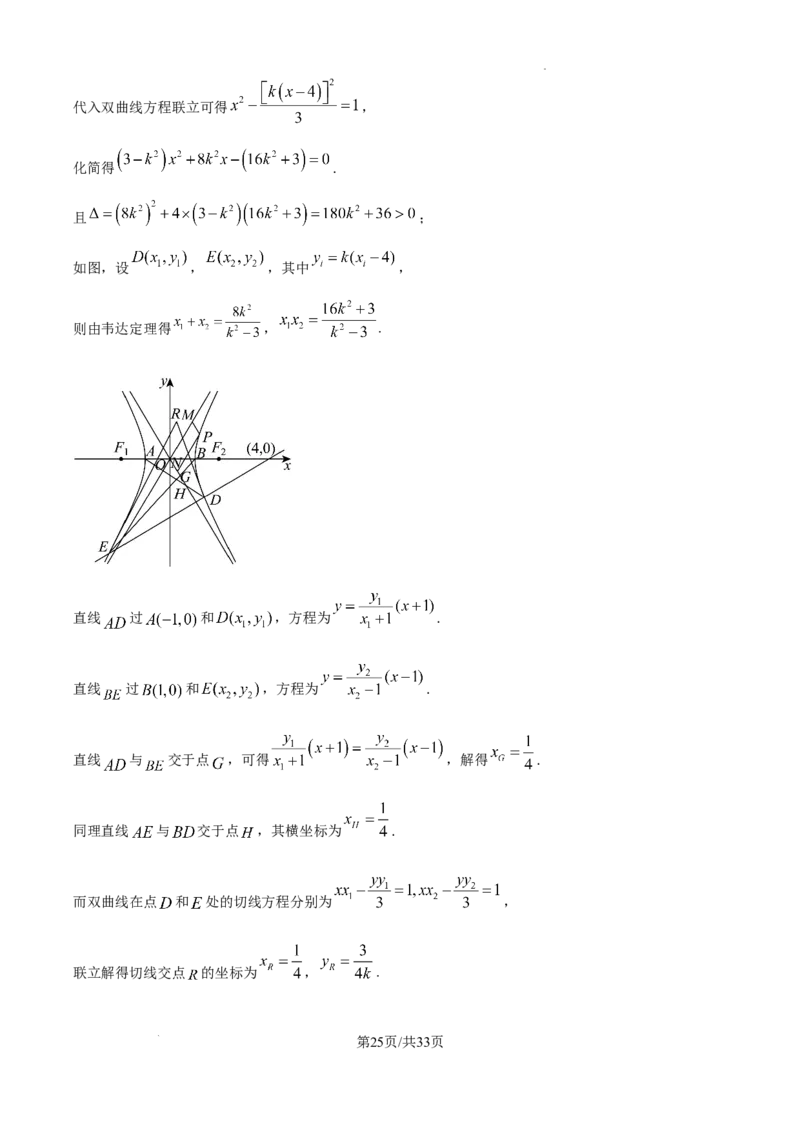
如图,设 , ,其中 ,
则由韦达定理得 , .
直线 过 和 ,方程为 .
直线 过 和 ,方程为 .
直线 与 交于点 ,可得 ,解得 .
同理直线 与 交于点 ,其横坐标为 .
而双曲线在点 和 处的切线方程分别为 ,
联立解得切线交点 的坐标为 , .
第25页/共33页
学科网(北京)股份有限公司因此,点 , , 均在直线 上;
设 , , .
由中点坐标公式得中点坐标为
,
故 为 和 的中点,即 ,因此 .
18. 在一个不透明的袋子中,装有 个形状大小相同、颜色互不相同的小球,某人先后两次任意摸
取小球(每次至少摸取1个小球),第一次摸取后记录摸到的小球颜色,再将摸到的小球放回袋中;第二
次摸取后,也记下摸取到的小球颜色.
(1)求某种特定颜色两次都被记下的概率;
(2)设第一次摸出 个球,两次摸球后,恰有 种颜色两次都被记下.
①求 的分布列;②当 时,求 .
【答案】(1)
第26页/共33页
学科网(北京)股份有限公司(2)① , .
② .
【解析】
【分析】(1)先计算总的摸球情况数,再计算恰有一种特定颜色两次都被记下的情况数,最后利用古代
古典概型公式计算概率.
(2)根据分布列的定义求 的分布列,当 时,代入求得 .
【小问1详解】
第一次摸球,从 个球中至少摸一个球,情况数为 ;第二次摸球同样有 种情况.
则两次摸球的总的可能情况数为 .
除了特定的颜色的球外,对于剩下的 种颜色,第一次摸球是少摸一个球,有 种情况;
第二次摸球至少摸一个球,也有 种情况.所以对于这 种颜色,两次摸球的情况数为 .
那么特定颜色的球两次都被记录下来的情况数为 .
根据古典概型的概率计算公式,则特定颜色颜色两次都被记录下来的概率为:
.
【小问2详解】
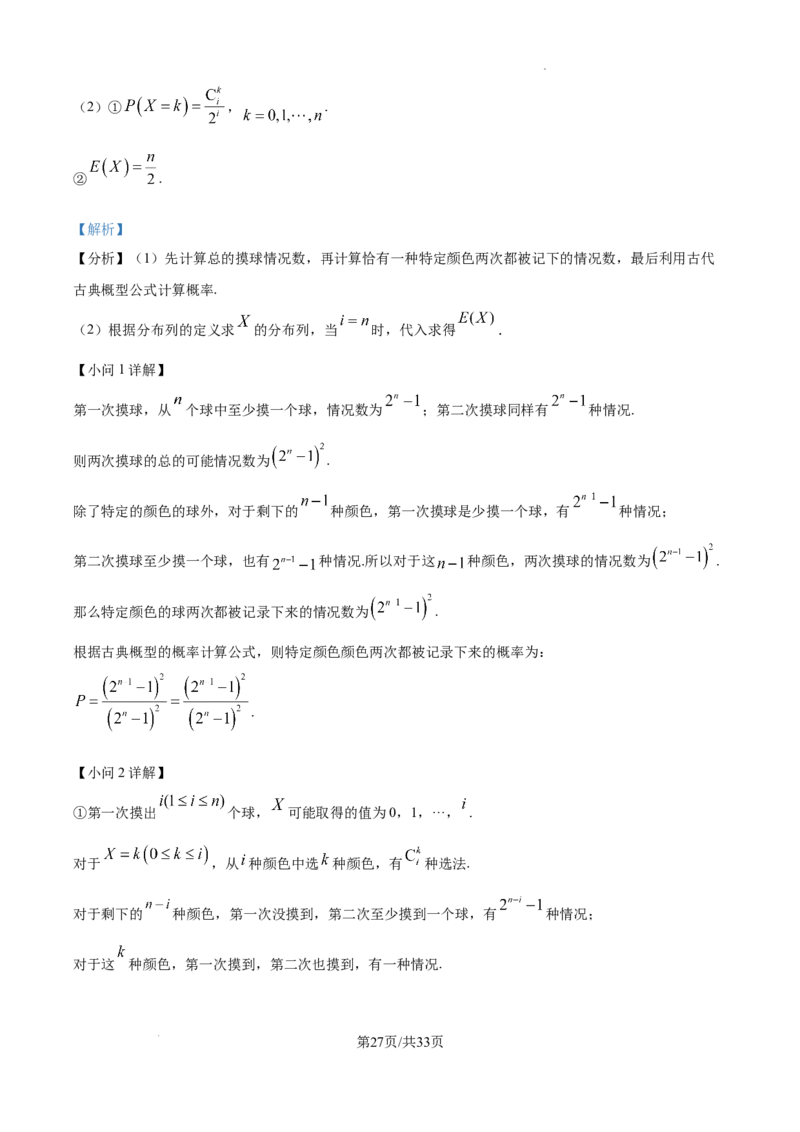
①第一次摸出 个球, 可能取得的值为0,1,···, .
对于 ,从 种颜色中选 种颜色,有 种选法.
对于剩下的 种颜色,第一次没摸到,第二次至少摸到一个球,有 种情况;
对于这 种颜色,第一次摸到,第二次也摸到,有一种情况.
第27页/共33页
学科网(北京)股份有限公司所以 , .
②当 时, 可能取得的值为0,1,···, .
因为根据期望公式 ,可以得到 .
19. 已知函数 有三个零点 ,满足 .
(1)求实数a的取值范围;
(2)若 为 上任意 个实数, ,当
且仅当 时等号成立,则称函数 在 上为“凸函数”.也可设可导函数 在
上的导函数为 在 上的导函数为 ,当 时,函数 在 上
的为“凸函数”.若 为 上任意 个实数,满足
,当且仅当 时等号成立,则称函数
在 上为“凹函数”.也可设可导函数 在 上的导函数为 在 上的导
函数为 ,当 时,函数 在 上的为“凹函数”.这里关于凹凸函数的不等式即为
著名的琴生不等式,请根据以上材料,回答下面的问题.
(i)若函数 为凸函数,求b的取值范围;
(ii)证明∶ .
【答案】(1)
第28页/共33页
学科网(北京)股份有限公司(2)(i) ;(ii)证明见解析.
【解析】
【分析】(1)由题目信息可判断 单调性,从而可得 ,然后讨论 ,2大小关系,可得
单调性,再结合零点存在性定理可得答案;
(2)(i)由题可得 ,对定义域恒成立,通过换元及复合函数导数求法可得
, 据 此 可 得 答 案 ; ( ii ) 由 题 目 信 息 , 结 合 令
可 得
,然后由
(i)中结论可完成证明.
【小问1详解】
由题 ,由题目信息:
,则 .
从而 在 上单调递减,在 上单调递增,从而 .
若 ,则 ,则 在 上单调递增,
又注意到 ,则此时 只有1个零点,不满足题意;
若 ,则 ,
第29页/共33页
学科网(北京)股份有限公司令 在
上单调递增,则 .
,又 ,则存在 ,
使 .
结合 单调性可得, .
则 在 上单调递增,在 上单调递减.
,
则 .
令 ,则 ,
从而 在 上单调递减,又 ,
则 .
又注意到 , , ,
,则存在 ,
使 ,满足题意.
所以实数 的取值范围是 ;
【小问2详解】
(i)令 ,则 ,
第30页/共33页
学科网(北京)股份有限公司从而 ,
令 ,则 ,
从而 ,由题 ,对定义域恒成立,
则 恒成立,
即 .
令 ,则 ,
令 ,则 ,
从而 , ,
则 在 上单调递增,在 上单调递减,则 ,
从而 ,
所以实数 的取值范围是 ;
(ii)由题目信息, ,当且仅当 时取等号.
由(1), ,
第31页/共33页
学科网(北京)股份有限公司又注意到 ,
则 .
令 ,
则
则 ,
即 ,
即
.
因 ,则 ,
因 ,则 , ,
则 ,从而
,则取 时,
即 时,
第32页/共33页
学科网(北京)股份有限公司,
即 .
第33页/共33页
学科网(北京)股份有限公司