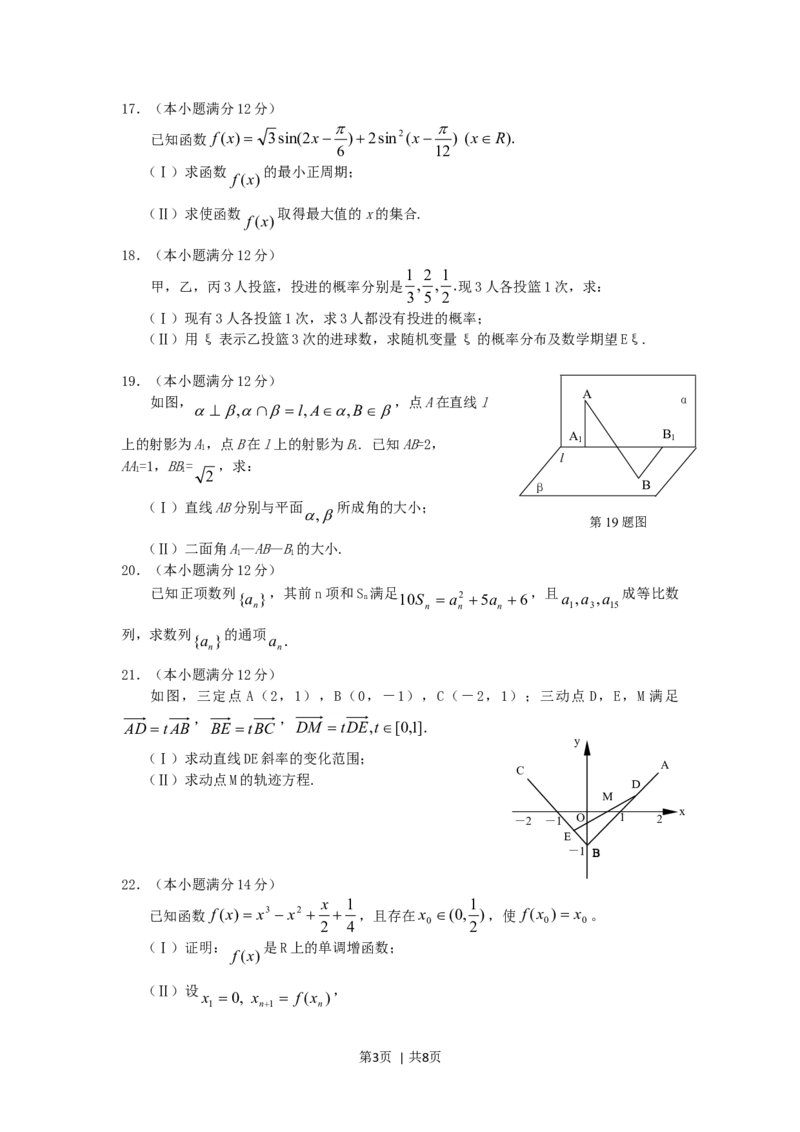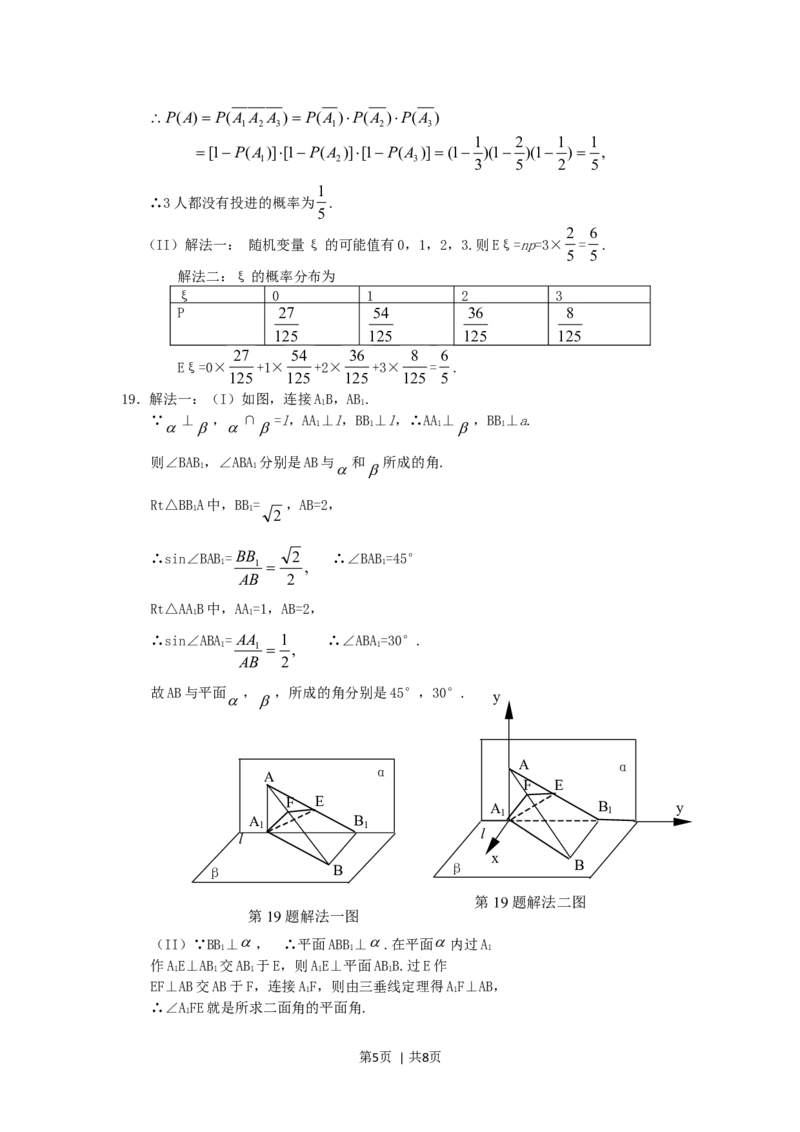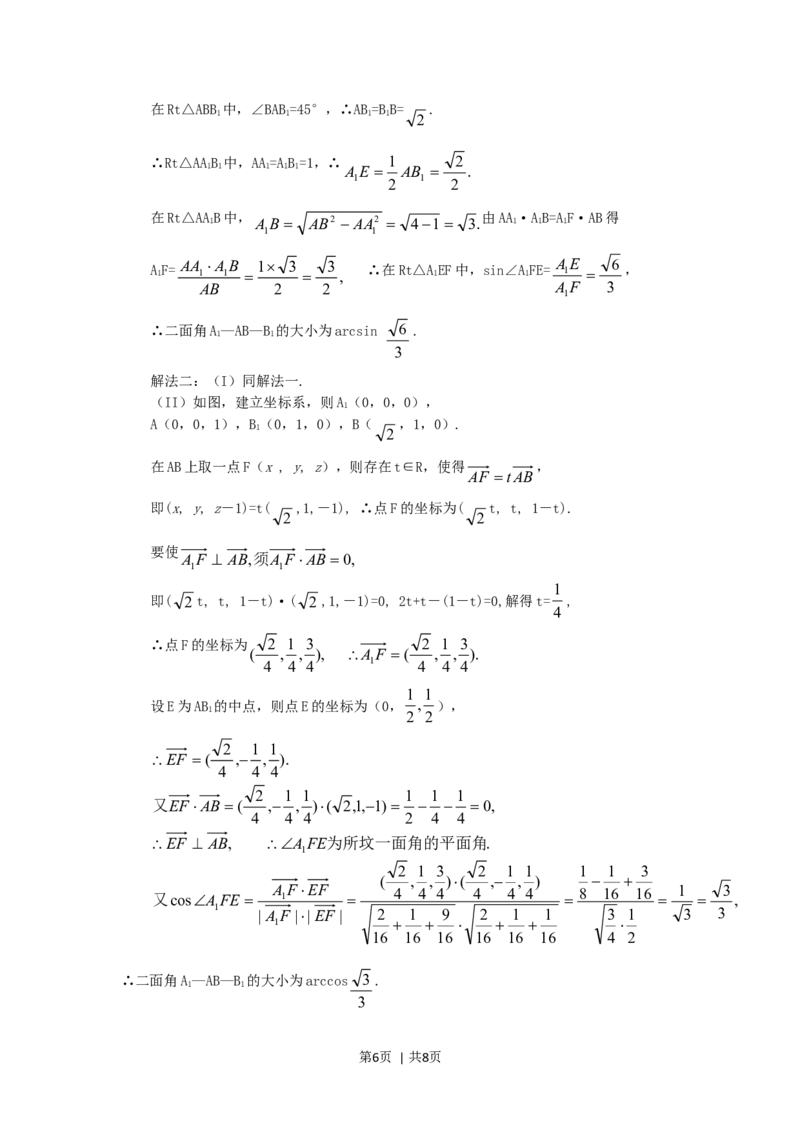2006年陕西高考理科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·word_陕西

2006 年陕西高考理科数学真题及答案 注意事项： 1．本试卷分第一部分和第二部分。第一部分为选择题，第二部分为非选择题。 2．考生领到试卷后，须按规定在试卷上填写姓名、准考证号，并在答题卡上填涂对 应的试卷类型信息点。 3．所有答案必须在答题卡指定区域内作答，考试结束后，将本试卷和答题卡一并交回。 第一部分 选择题（共60分） 一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的（本大题共12小 题， 每小题5分，共60分）。 1．已知集合 等于 P {xN |1 x 10},集合Q {xR| x2  x6  0},则PQ （A）{1，2，3} （B）{2，3} （C）{1，2} （D）{2} 2．复数(1i)2 等于 1i （A）1+i （B）―1―i （C）1―i （D）―1+i 1 3．lim 等于 n2n( n2 1 n2 1) 1 1 （A）0 （B） （C） （D）1 4 2 4．设函数 的图像过点（2，1），其反函数的图像过点 f(x)  log (xb)(a  0,a 1) a （2，8），则a+b等于 （A）3 （B）4 （C）5 （D）6 5．设直线过点（0，a）其斜率为1，且与圆x2+y2=2相切，则a的值为 （A）±4 （B） （C）±2 （D） 2 2  2 6．“α、β、成等差数列”的“等式sin(α+ )=sin2β成立”的是 （A）充分而不必要条件 （B）必要而不充分条件 （C）充分必要条件 （D）既不充分又不必要条件 x2 y2  7．已知双曲线  1(a 2)的两条渐近线的夹角为 ,则双曲线的离心率为 a2 2 3 （A）2 3 （B）2 6 （C） （D）2 3 3 3 第1页 | 共8页1 a 8．已知不等式 对任意正实数x,y恒成立，则正实数a的最小值为 (x y)(  )9 x y （A）8 （B）6 （C）4 （D）2 9．已知非零向量 满足 AB与AC （ AB AC ）· =0 且 AB · AC = 1 .  BC | AB| | AC| | AB| | AC| 2 则△ABC为 （A）等边三角形 （B）直角三角形 （C）等腰非等边三角形 （D）三边均不相等的三角形 10．已知函数 . 若 ， =1－a，则 f(x)  ax2 2ax4(0 a 3) x  x x  x 1 2 1 2 （A） （B） f(x )  f(x ) f(x ) f(x ) 1 2 1 2 （C） （D） 的大小不能确定 f(x )  f(x ) f(x )与f(x ) 1 2 1 2 11．已知平面外不共线的三点A，B，C到的距离都相等，则正确的结论是 （A）平面ABC必平行于 （B）平面ABC必不垂直于 （C）平面ABC必与相交 （D）存在△ABC的一条中位线平行于或在内 12．为确保信息安全，信息需加密传输，发送方由明文→密文（加密），接收方由密文→ 明 文（解密）. 已知加密规则为：明文a,b,c,d对应密文a+2b,2b+c,2c+3d,4d. 例如， 明文1,2,3,4对应密文5,7,18,16. 当接收方收到密文14,9,23,28时，则解密得到的明 文为 （A）7,6,1,4 （B）6,4,1,7 （C）4,6,1,7 （D）1,6,4,7 第二部分（共90分） 二．填空题：把答案填在答题卡相应题号后的横线上（本大题共4小题，每小题4分，共 16分）. 13．cos43cos77 sin43cos167的值为 . 1 14．（3x ）12展开式中x－1的系数为 （用数字作答）. x 15．水平桌面α上放有4个半径均为2R的球,且相邻的球都相切(球心的连线构成正方形). 在这4个球的上面放1个半径为R的小球，它和下面的4个球恰好都相切，则小球的 球心到水平桌面α的距离是 . 16．某校从8名教师中选派4名教师同时去4个边远地区支教（每地1人），其中甲和 乙不同去，甲和丙只能同去或同不去，则不同的选派方案共有 种（用数 学作答）. 三．解答题：解答应写出文字说明，证明过程或演算步骤（本大题共6小题，共74分） 第2页 | 共8页17．（本小题满分12分）   已知函数 f(x)  3sin(2x )2sin2(x ) (xR). 6 12 （Ⅰ）求函数 的最小正周期； f(x) （Ⅱ）求使函数 取得最大值的x的集合. f(x) 18．（本小题满分12分） 1 2 1 甲，乙，丙3人投篮，投进的概率分别是 , , .现3人各投篮1次，求： 3 5 2 （Ⅰ）现有3人各投篮1次，求3人都没有投进的概率； （Ⅱ）用ξ表示乙投篮3次的进球数，求随机变量ξ的概率分布及数学期望Eξ. 19．（本小题满分12分） A 如图， ，点A在直线l α ,l,A,B 上的射影为A，点B在l上的射影为B. 已知AB=2， A 1 B 1 1 1 l AA=1，BB= ，求： 1 1 2 β B （Ⅰ）直线AB分别与平面 所成角的大小； , 第19题图 （Ⅱ）二面角A—AB—B的大小. 1 1 20．（本小题满分12分） 已知正项数列 ，其前n项和S 满足 ，且 成等比数 {a } n 10S  a2 5a 6 a ,a ,a n n n n 1 3 15 列，求数列 的通项 {a } a . n n 21．（本小题满分12分） 如图，三定点 A（2，1），B（0，－1），C（－2，1）；三动点 D，E，M 满足 ， ， AD tAB BE tBC DM tDE,t[0,1]. y （Ⅰ）求动直线DE斜率的变化范围； A C （Ⅱ）求动点M的轨迹方程. D M x －2 －1 O 1 2 E －1 BB 22．（本小题满分14分） x 1 1 已知函数 f(x)  x3 x2   ，且存在x (0, )，使 f(x )  x 。 2 4 0 2 0 0 （Ⅰ）证明： 是R上的单调增函数； f(x) （Ⅱ）设 ， x  0, x  f(x ) 1 n1 n 第3页 | 共8页1 y  , y  f(y ) 1 2 n1 n 其中n=1，2，… 证明： ； x  x  x  y  y n n1 0 n1 n 1 y x 1 （Ⅲ）证明： n1 n1  . y x 2 n n 2006年陕西高考理科数学真题参考答案 一、选择题（本大题共12小题，每小题5分，共60分）. 1.B 2.C 3.B 4.C 5.B 6.A 7.D 8.B 9.D 10.A 11.D 12.C 二、填空题：（本大题共4小题，每小题4分，共16分）. 1 13. 14.594 15.3R 16. 600 2 三、解答题：（本大题共6小题，共74分）.   17．解：（I） f(x)  3sin2(x )1cos2(x ) 12 12 3  1   2[ sin2(x ) cos2(x )]1 2 12 2 12    2sin[2(x ) ]1 12 6   2sin(2x )1. 3 2 T  . 2  （II）当f(x)取最大值时,sin(2x ) 1,有 3   2x  2k , 3 2 5 即x  k (kZ), 12 5 所求x的集合为{xR| x  k , kZ}. 12 18．解：（I）记“甲投篮1次投进”为事件A ，“乙投蓝1次投进”为事件A ，“丙投篮 1 2 1 次 投 进 ” 为 事 件 A ， “ 3 人 都 没 有 投 进 ” 为 事 件 A. 则 3 1 2 1 P(A )  ,P(A )  ,P(A )  . 1 3 2 5 3 2 第4页 | 共8页P(A)  P(A A A )  P(A )P(A )P(A ) 1 2 3 1 2 3 1 2 1 1 [1P(A )][1P(A )][1P(A )](1 )(1 )(1 )  , 1 2 3 3 5 2 5 1 ∴3人都没有投进的概率为 . 5 2 6 （II）解法一： 随机变量ξ的可能值有0，1，2，3.则Eξ=np=3× = . 5 5 解法二：ξ的概率分布为 ξ 0 1 2 3 P 27 54 36 8 125 125 125 125 27 54 36 8 6 Eξ=0× +1× +2× +3× = . 125 125 125 125 5 19．解法一：（I）如图，连接AB，AB. 1 1 ∵ ⊥ ， ∩ =l，AA⊥l，BB⊥l，∴AA⊥ ，BB⊥a.     1 1 1  1 则∠BAB，∠ABA 分别是AB与 和 所成的角. 1 1   Rt△BBA中，BB= ，AB=2， 1 1 2 ∴sin∠BAB= BB 2 ∴∠BAB=45° 1 1  , 1 AB 2 Rt△AAB中，AA=1，AB=2， 1 1 ∴sin∠ABA= AA 1 ∴∠ABA=30°. 1 1  , 1 AB 2 故AB与 平面  ，  ，所成的角分别是45°，30°. y A α A α F E F E A 1 B 1 y A B 1 1 l l x β B β B 第19题解法二图 第19题解法一图 （II）∵BB⊥， ∴平面ABB⊥.在平面内过A 1 1 1 作AE⊥AB 交AB 于E，则AE⊥平面ABB.过E作 1 1 1 1 1 EF⊥AB交AB于F，连接AF，则由三垂线定理得AF⊥AB， 1 1 ∴∠AFE就是所求二面角的平面角. 1 第5页 | 共8页在Rt△ABB 中，∠BAB=45°，∴AB=BB= . 1 1 1 1 2 ∴Rt△AAB 中，AA=AB=1，∴ 1 2 1 1 1 1 1 A E  AB  . 1 2 1 2 在Rt△AAB中， 由AA·AB=AF·AB得 1 A B  AB2  AA2  41  3. 1 1 1 1 1 A 1 F= AA 1 A 1 B  1 3  3 , ∴在Rt△A 1 EF中，sin∠A 1 FE= A 1 E  6 ， AB 2 2 A F 3 1 ∴二面角A—AB—B 的大小为arcsin 6 . 1 1 3 解法二：（I）同解法一. （II）如图，建立坐标系，则A（0，0，0）， 1 A（0，0，1），B（0，1，0），B（ ，1，0）. 1 2 在AB上取一点F（x , y, z），则存在t∈R，使得 ， AF tAB 即(x, y, z－1)=t( ,1,－1), ∴点F的坐标为( t, t, 1－t). 2 2 要使 A F  AB,须A F AB  0, 1 1 1 即( 2 t, t, 1－t)·( 2 ,1,－1)=0, 2t+t－(1－t)=0,解得t= , 4 ∴点F的坐标为 2 1 3 2 1 3 ( , , ), A F ( , , ). 4 4 4 1 4 4 4 1 1 设E为AB 的中点，则点E的坐标为（0， , ）， 1 2 2 2 1 1 EF ( , , ). 4 4 4 2 1 1 1 1 1 又EFAB ( , , )( 2,1,1)    0, 4 4 4 2 4 4 EF  AB, A FE为所坟一面角的平面角. 1 2 1 3 2 1 1 1 1 3 ( , , )( , , )   A FEF 4 4 4 4 4 4 8 16 16 1 3 又cosA FE  1     , 1 | A F || EF | 2 1 9 2 1 1 3 1 3 3 1       16 16 16 16 16 16 4 2 ∴二面角A—AB—B 的大小为arccos 3 . 1 1 3 第6页 | 共8页20．解： ① 解之得a=2或a=3. 10S  a2 5a 6, 10a  a2 5a 6, 1 1 n n n 2 1 1 又 ② 10S  a2 5a 6 (n  2) n1 n1 n1 由①—②得 10a (a2 a2 )5(a a ),即(a a )(a a 5)  0 n n n1 n n1 n n1 n n1  a a 0, a a 5(n 2). 当a 3时,a 13,a 73. n n1 n n1 1 3 15 a ,a ,a 不成等比数列,a 3.当a  2时,a 12,a 72,有a2  a a , 1 3 15 1 1 3 15 3 1 15 a  2, a 5n3 1 n 21．解：（I） y 解法一：如图（1）设D(x, y), E(x , y), M(x, y). D D E E A C 由 AD tAB,BE tBC,知(x 2,y 1) t(2,2), D D M D x  2t 2, x  2t, x  D 同理  E －2 －1 O 1 2 y  2t 1. y  2t 1.  D  E E y  y 2t 1(2t 1) －1 BB k  E D  12t. DE x x 2t (2t 2) E D 第21题解法图  t[0,1], k [1,1]. DE （II）  DM tDE, (x2t 2,y2t 1) t(2t 2t 2,2t 12t 1) t(2,4t 2) (2t,4t2 2t), x  2(12t), x2  y  ,即x2  4y. y (12t)2, 4  t[0,1],x  2(12t)[2,2] 即所求轨迹方程为 x2  4y,x[2,2]. 解法二：（I）同上. （II）如图， OD OA AD OAtAD OAt(OBOA) (1t)OAtOB, OE OBBE OBtBC OBt(OCOB) (1t)OBtOC, OM ODDM ODtDE ODt(OEOD) (1t)ODtOE (1t)2OA2(1t)tOBt2OC. 设M点坐标为(x, y)，由 得 OA (2,1),OB  (0,1),OC  (2,1) 第7页 | 共8页x (1t)2 22(1t)t0t2 (2)  2(12t),  消去t得x2  4y,  y (1t)2 12(1t)t(1)t2 1(12t)2,  t[0,1],x[2,2], 故轨迹方程是 x2  4y,x[2,2] 1 1 1 22．解：（I） f (x) 3x2 2x 3(x )2  0, ∴ f(x)是R上的单调增函 2 3 6 数. 1 （II） 0 x  ,即x  x  y .又f(x)是增函数, f(x ) f(x ) f(y ), 0 2 1 0 1 1 0 1 1 即x  x  y ,又x  f(x )  f(0)  0 x , 2 0 2 2 1 4 1 1 3 1 y  f(y )  f( )    y . 2 1 2 8 2 1 综上,x  x  x  y  y . 1 2 0 2 1 用数学归纳法证明如下：（1）当n=1时，上面已证明成立. （2）假设当n=k （k≥1）时有 x  x  x  y  y . k k1 0 k1 k 当 n=k+1 时 ， 由 f(x) 是 单 调 增 函 数 ， 有 f(x ) f(x ) f(x ) f(y ) f(y ), k k1 0 k1 k x  x  x  y  y . k1 k2 0 k2 k1 由（1）和（2）对一切n=1，2，…，都有 x  x  x  y  y . n n1 0 n1 n y x f(y ) f(x ) 1 （III） n1 n1  n n  y2  x y  x2 (y  x ) y x y x n n n n n n 2 n n n n 1 (y  x )2 (y  x ) n n n n 2 1 1 [(y  x ) ]2  . n n 2 4 1 1 1 由（II）知 0 y  x 1,  y  x   n n 2 n n 2 2 y x 1 1 1  n1 n1 ( )2   . y x 2 4 2 n n 第8页 | 共8页