文档内容
第八单元测试卷(一)
一、先计算下面各题,再找出规律。
+ + = + + + = + + + + =
二、六(1)班有八名同学进行乒乓球比赛,如果每两名同学之间都要进行一场比赛,
一共要比赛多少场?怎样推算呢?
从简单的情况开始研究,运用画图法解答:
……
③1+ ④1+
②1+
①1 2+3= 2+3+ ……
2=3
6 4=10
三、观察图中的点阵图和相应的等式,探究其中的规律,在④和⑤后面的横线上分
别写出相应的等式。
……
①1= ②1+3 ③1+3
④ ⑤ ……
12 =22 +5=32
四、观察下列图形,按规律把算式补充完整。
…… …… ……
⑥25
②1+ ③4+ ④9+ ⑤16 ⑦36+
①1 +
3 5 7 +
五、观察点阵中的规律,填一填。
…… …… ……
②1+ ③1+ ④1+ ⑤1+ ⑥1+ ⑦1+
①1
4 8 12
六、如图依次排列着5盏灯,用不同位置上亮灯和灭灯表示一个具体的数(亮灯用□表示,灭灯用■表示)。请根据下面前四种状况所表示的数,完成下列问题。
写出图⑤表示的数。在图⑥中画出亮灯和灭灯的状况。
七、把边长为1厘米的正方形纸片,按下面的规律拼成长方形:
1.用5个正方形拼成的长方形的周长是多少厘米?
2.用m个正方形拼成的长方形的周长是多少厘米?
八、观察点阵与算式的对应规律,并填空。
…… ……
③1+4 ④1+4 ⑤…
①1 ②1+4 ⑥
+4 +4+4 …
第⑥个点阵图中有多少个点?
九、如图是用棋子摆成的图案,摆第1个图案需要7枚棋子,摆第2个图案需要19
枚棋子,摆第3个图案需要37枚棋子,按照这样的方式摆下去,则摆第10个图案
需要多少枚棋子?
…… ……
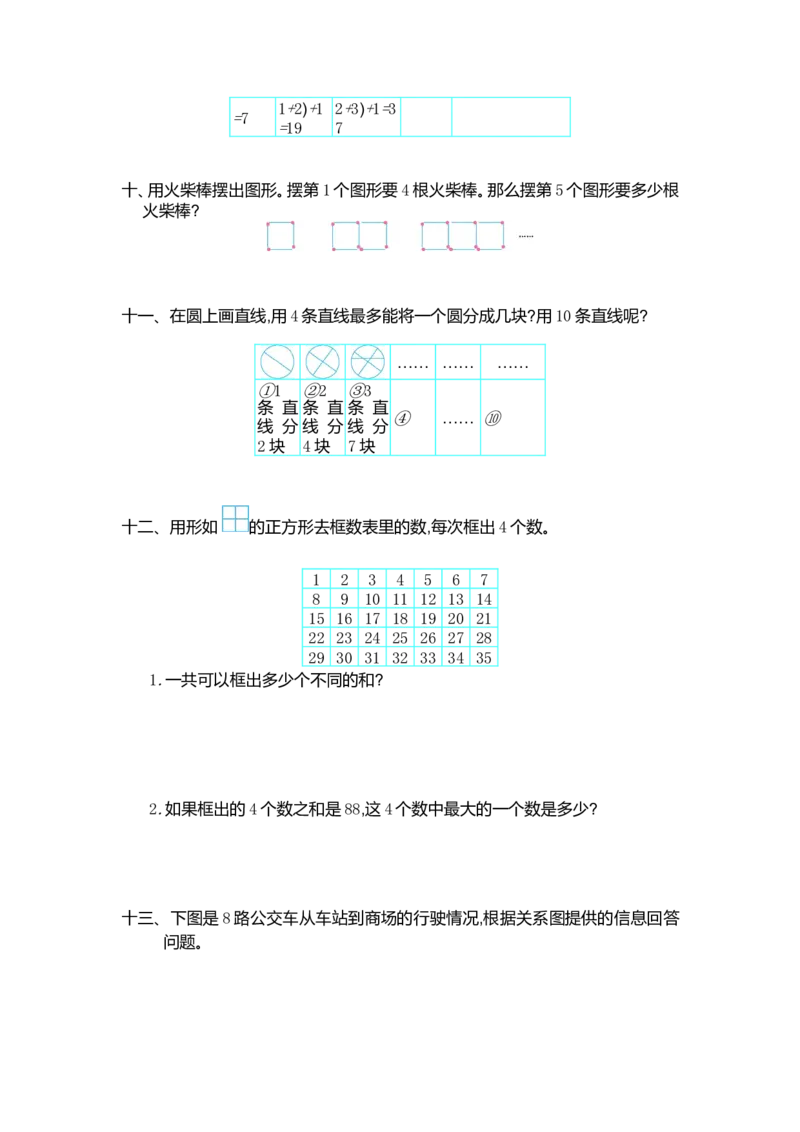
①6+1 ②6×( ③6×(1+ …… ⑩1+2)+1 2+3)+1=3
=7
=19 7
十、用火柴棒摆出图形。摆第1个图形要4根火柴棒。那么摆第5个图形要多少根
火柴棒?
十一、在圆上画直线,用4条直线最多能将一个圆分成几块?用10条直线呢?
…… …… ……
①1 ②2 ③3
条 直 条 直 条 直
④ …… ⑩
线 分 线 分 线 分
2块 4块 7块
十二、用形如 的正方形去框数表里的数,每次框出4个数。
1 2 3 4 5 6 7
8 9 10 11 12 13 14
15 16 17 18 19 20 21
22 23 24 25 26 27 28
29 30 31 32 33 34 35
1.一共可以框出多少个不同的和?
2.如果框出的4个数之和是88,这4个数中最大的一个数是多少?
十三、下图是8路公交车从车站到商场的行驶情况,根据关系图提供的信息回答
问题。1.公交车从车站到商场共行驶了( )分钟。
2.在前3分钟,公交车的速度从0提高到( )米/分。
3.从( )分到( )分,公交车的速度保持不变,每分钟行驶( )米。
4.从( )分到( )分,公交车的速度在减小。
参考答案
一、从 图形中,我们已经研究得出:这种后一个加数是前一个加数的一
半的连加算式的和是1减最后一个加数的差,即分母是最后一个加数的分母,分子
比分母少1。利用这个规律,我们可以快速计算出每个算式的结果。
+ + = + + =
1- + - + - =1- =
+ + + = + + + =1- + - + - + - =1- =+ + + + = + + + + =1- + - + - + - + - =1- =
二、因为3人比2人增加2场;4人比3人增加3场;5人比4人增加4场……所以8
人比赛的场数是1+2+3+…+7=28(场)。
三、 ④1+3+5+7=42 ⑤1+3+5+7+9=52
四、 ⑤16+9 ⑥25+11 ⑦36+13
五、观察前四幅图可得,第一幅图是 1 个点;第二幅图是 1+4(个)点,可以写作
1+1×4;第三幅是1+8(个)点,可以写作1+2×4;第四幅图是1+12(个)点,可以写作
1+3×4;由此可得第 n幅图,有1+(n-1)×4(个)点,由此即可解决问题。当 n=5时,
1+(5-1)×4=1+16;当n=6时,1+(6-1)×4=1+20;当n=7时,1+(7-1)×4=1+24。
六、由前四幅图可知:当灯灭时(■):从右边向左,第一个灯表示1;第二个灯表示3;
第三个灯表示9;第五个灯表示81;1×3=3,3×3=9,后一个数是前一个的3倍,那么
第四个灯表示9×3=27;当灯亮时□所表示的数不显示。那么,⑤中灭的灯是从右
边数的第三、四、五这三个,就表示9+27+81=117。
⑥93=81+9+3,应是从右边数的第二、三、五这三个灯熄灭:
七、观察图形,
2个正方形拼接,周长是1×6(厘米)=2×2+2(厘米),
3个正方形拼接,周长是1×8(厘米)=3×2+2(厘米),
4个正方形拼接,周长是1×10(厘米)=4×2+2(厘米)。
由此发现,每多增加一个正方形,大长方形周长增加2个边长的长。大长方形的周
长等于小长方形个数2倍加2厘米。
1.用5个正方形拼成的长方形的周长是5×2+2=12(厘米)
2.用m个正方形拼成的长方形的周长是(2m+2)厘米。
八、根据题干中的已知图形中点数特点,可以探索出这组图形的一般规律,并利用
规律进行解答。
观察图形可得:第一个图形有1个点,可以写作1+(1-1)×4;
第二个图形有1+4(个)点,可以写作1+(2-1)×4;
第三个图形有1+4+4(个)点,可以写作1+(3-1)×4……
则第n个图形的点数就可以写作1+(n-1)×4。
当n=6时,点数为1+(6-1)×4=21(个)
九、第1个需棋子7
第2个需棋子19;相差12;6的2倍;
第3个需棋子37;相差18;6的3倍;
第4个需棋子61;相差24;6的4倍;
……
第n个需棋子3n(n+1)+1;相差6n;6的n倍。
所求摆第10个图案需要的棋子:3n(n+1)+1=3×10×(10+1)+1=331。
十、根据火柴棒的摆设规律可知,多摆一个正方形就需要加三根火柴棒。
第1个图形需要4根火柴棒;
第2个图形需要4+3×1=7(根)火柴棒;
第3个图形需要4+3×2=10(根)火柴棒;
摆n个图形需要4+3×(n-1)=3n+1(根)火柴棒。
当n=5时,需要3×5+1=16(根)火柴棒。
十一、数形结合,观察图形,画1条直线将圆分为2块,即增加了1块;画2条直线,当2条直线不相交时,增加了1块;当2条直线相交时,增加了2块,此看出,要想分成
的块数尽量多,应当使后画的直线尽量与前面已画的直线相交;再画第3条直线时,
应当与前面2条直线都相交,这样又增加了3块;画第4条直线时,应当与前面3条
直线都相交,这样又增加了 4 块。所以 4 条直线最多将一个圆分成
1+1+2+3+4=11(块)。
由上面的分析可以看出,画第n条直线时,应当与前面已画的(n—1)条直线都相交,
此时将增加n块。因为一开始的圆算1块,所以n条直线最多将圆分成
1+(1+2+3+…+n)=1+ (块)。
当n=10时,可分成1+ =56(块)。
十二、1.横着看,第一行和第二行一共有6种不同的框法,由于这些数自左向右都
是逐渐增大的,所以就会框出6种不同的和;竖着看,第一列和第二列一共有 4种
不同的框法,由于这些数自上向下都是逐渐增大的,所以就会框出4种不同的和;
再用6乘4就是框出不同和的个数,6×4=24(个);
2.从表格中可看出框的4个数,左右相邻的差1,上下相邻的差7,设最小的数是x,
右边的就为x+1,x下面的就为x+7,x+7右边的为x+8。由它们的和是88列出方程
求解。
解:设最小的数是x,由题意得:
x+x+1+x+7+x+8=88 x=18
最大的数是18+8=26
十三、1.8 2.400 3.3 7 400 4.7 8