文档内容
5.1任意角和弧度制
1. 任意角;2. 终边相同的角;3. 终边在某条直线上的角的集合;4. 区域角的表示;5. 分角、倍角所
在角限的判断;6. 有关“角度”与“弧度”概念的理解;7. 角度制与弧度制的转化; 8. 用弧度制表示
区域角;9. 求扇形面积最值的函数思想.
一、单选题
1.(2021·伊美区第二中学高一月考) 化为弧度是( )
A. B. C. D.
2.(2021·广东高一期末)下列各角中,与2021°终边相同的角为( )
A.41° B.129° C.219° D.﹣231°
3.(2021·永昌县第四中学高一期末)若α是第四象限角,则180°+α一定是( )
A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角
4.(2021·江西省铜鼓中学高一期末)一个扇形的圆心角为150°,面积为 ,则该扇形半径为
( )
A.4 B.1 C. D.2
5.(2021·永州市第四中学高一月考)在 的范围内,与 终边相同的角是( )
A. B. C. D.
6.(2021·山西平城·大同一中高一月考)已知扇形的周长为12cm,圆心角为 ,则此扇形的面积为
( ).
A.8cm2 B.10cm2 C.12cm2 D.14cm2
7.(2021·河南林州一中高一月考)已知集合A={α|α小于90°},B={α|α为第一象限角},则
A∩B=( )
A.{α|α为锐角} B.{α|α小于90°}C.{α|α为第一象限角} D.以上都不对
8.(2021·科尔沁左翼后旗甘旗卡第二高级中学高一期末)已知半径为1的扇形面积为 ,则扇形的圆
心角为( )
A. B. C. D.
9.(2021·山东潍坊·高一期末)已知某扇形的半径为 ,圆心角为 ,则此扇形的面积为
( )
A. B. C. D.
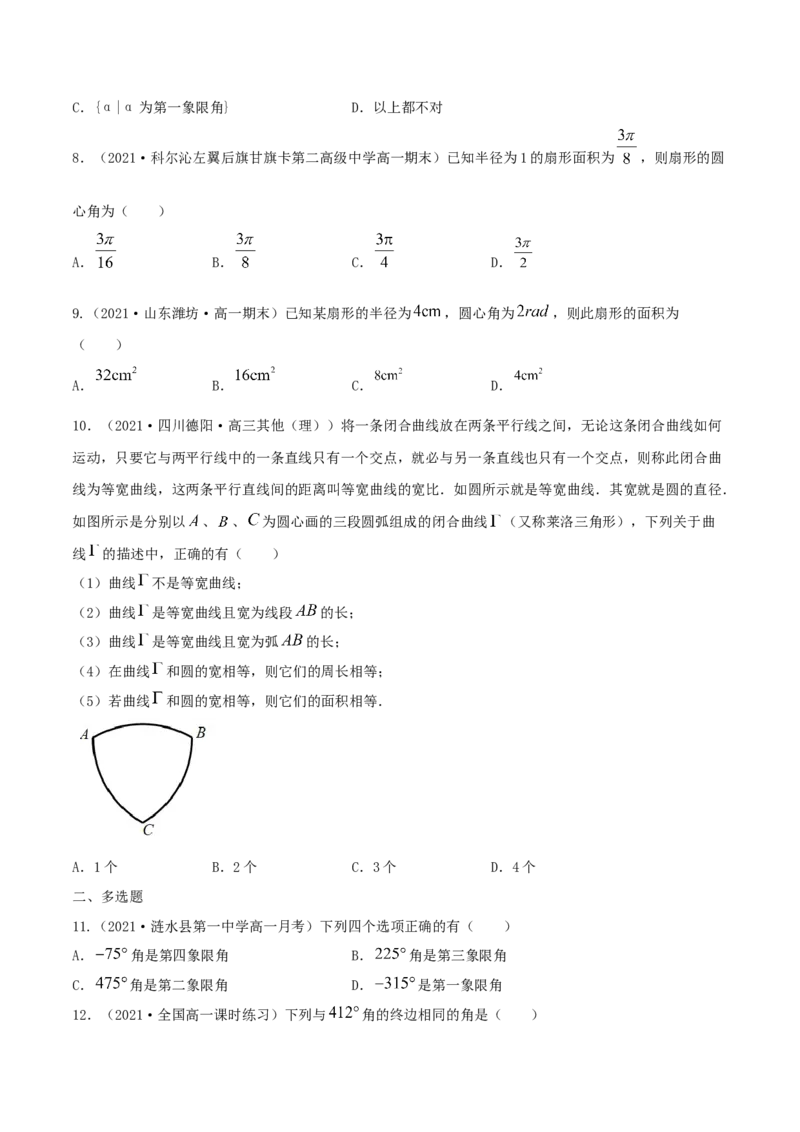
10.(2021·四川德阳·高三其他(理))将一条闭合曲线放在两条平行线之间,无论这条闭合曲线如何
运动,只要它与两平行线中的一条直线只有一个交点,就必与另一条直线也只有一个交点,则称此闭合曲
线为等宽曲线,这两条平行直线间的距离叫等宽曲线的宽比.如圆所示就是等宽曲线.其宽就是圆的直径.
如图所示是分别以 、 、 为圆心画的三段圆弧组成的闭合曲线 (又称莱洛三角形),下列关于曲
线 的描述中,正确的有( )
(1)曲线 不是等宽曲线;
(2)曲线 是等宽曲线且宽为线段 的长;
(3)曲线 是等宽曲线且宽为弧 的长;
(4)在曲线 和圆的宽相等,则它们的周长相等;
(5)若曲线 和圆的宽相等,则它们的面积相等.
A.1个 B.2个 C.3个 D.4个
二、多选题
11.(2021·涟水县第一中学高一月考)下列四个选项正确的有( )
A. 角是第四象限角 B. 角是第三象限角
C. 角是第二象限角 D. 是第一象限角
12.(2021·全国高一课时练习)下列与 角的终边相同的角是( )A. B. C. D.
13.(2021·全国高一课时练习)下列条件中,能使 和 的终边关于 轴对称的是( )
A. B.
C. D.
E.
14.(2021·重庆高一月考)设 是第三象限角,则 所在象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
三、填空题
15.(2021·宁县第二中学高一期中)已知角 的终边在图中阴影所表示的范围内(不包括边界),那么
________.
16.(2018·福建高一期中)已知扇形的面积为4,圆心角为2弧度,则该扇形的弧长为 .
17.(2021·上海杨浦·复旦附中高一月考)一个面积为1的扇形,所对弧长也为1,则该扇形的圆心角
是________弧度
四、双空题
18.(2021·上海高一课时练习) _________弧度; 弧度=________.
19.(2021·全国高一课时练习)(1)给出下列说法:
①锐角都是第一象限角;
②第一象限角一定不是负角;
③小于180°的角是钝角或直角或锐角.
其中正确说法的序号为________.(把正确说法的序号都写上)
(2)将时钟拨快20分钟,则分针转过的度数是________.20.(2021·浙江柯城·衢州二中高三一模)《九章算术》是中国古代的数学名著,其中《方田》一章给
出了弧田面积的计算公式.如图所示,弧田是由圆弧AB和其所对弦AB围成的图形,若弧田的弧AB长为
4π,弧所在的圆的半径为6,则弧田的弦AB长是__________,弧田的面积是__________.
21.(2021·宁波市北仑中学高一期中)已知扇形的周长为40,当它的圆心角为____时,扇形的面积最大,
最大面积为____.
五、解答题
22.(2021·全国高一课时练习)写出与α=-1910°终边相同的角的集合,并把集合中适合不等式-
720°≤β<360°的元素β写出来.
23.(2021·全国高一课时练习)写出终边在直线 上的角的集合.
24.(2021·全国高一课时练习)已知 为第二象限角,则 是第几象限角?
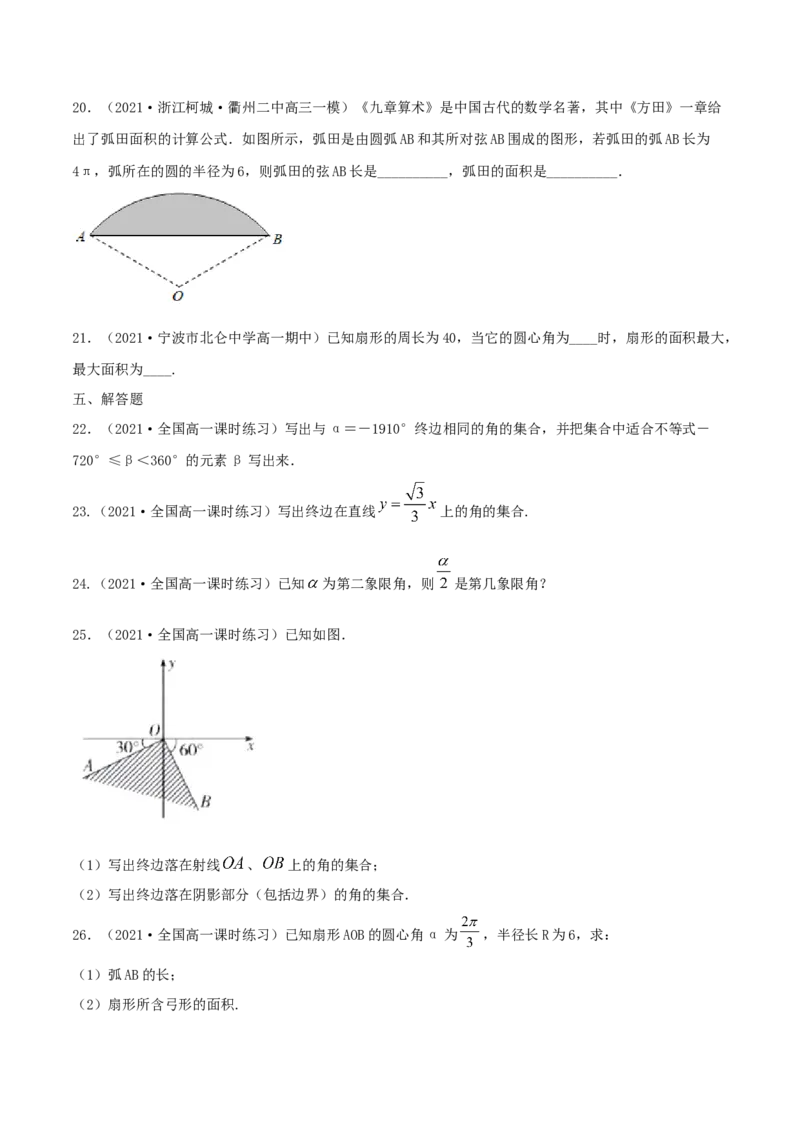
25.(2021·全国高一课时练习)已知如图.
(1)写出终边落在射线 、 上的角的集合;
(2)写出终边落在阴影部分(包括边界)的角的集合.
26.(2021·全国高一课时练习)已知扇形AOB的圆心角α为 ,半径长R为6,求:
(1)弧AB的长;
(2)扇形所含弓形的面积.27.(2021·浙江高一课时练习)已知一扇形的圆心角为 ,所在圆的半径为R.
(1)若 , ,求扇形的弧长及该弧所在的弓形的面积;
(2)若扇形的周长为20 cm,当扇形的圆心角 等于多少弧度时,这个扇形的面积最大?