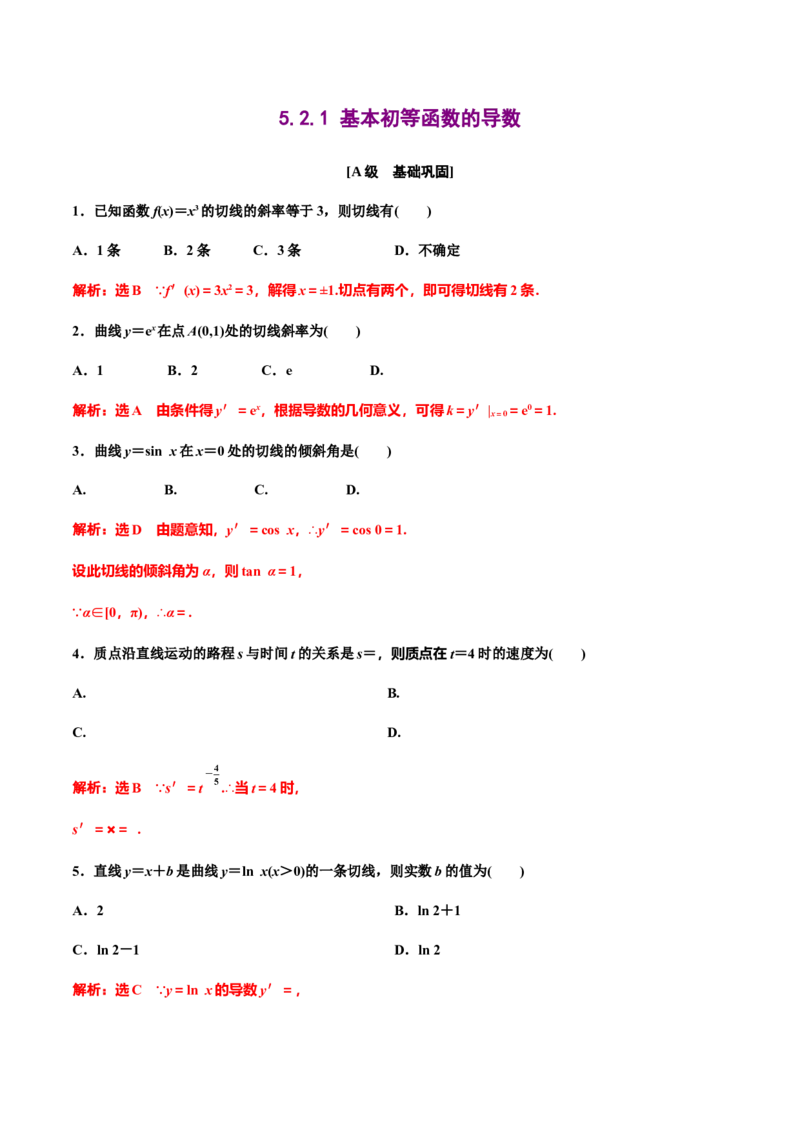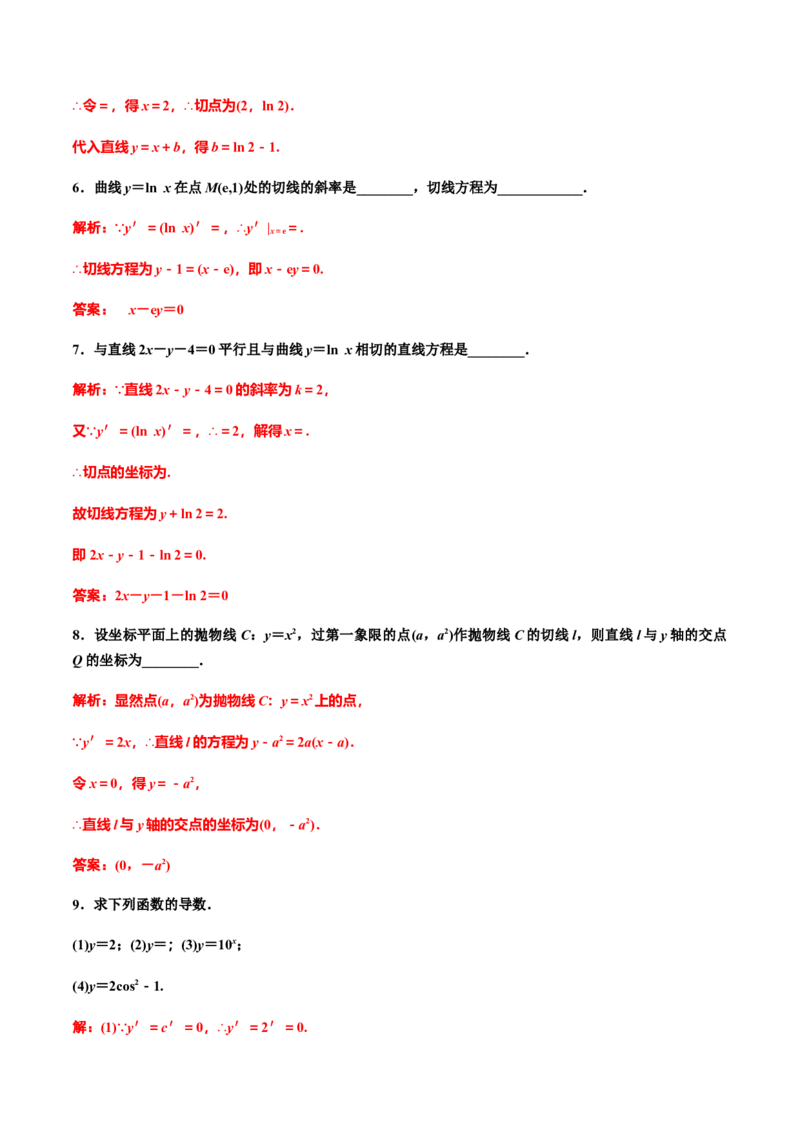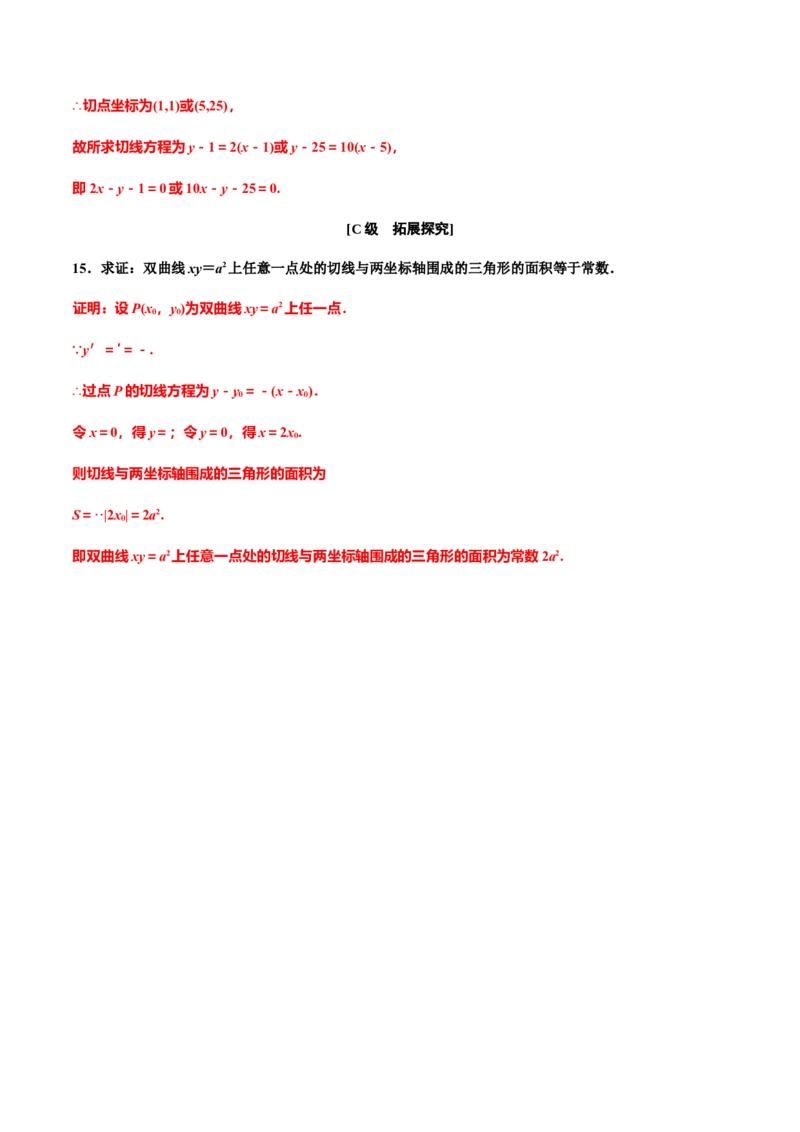文档内容
5.2.1 基本初等函数的导数
[A级 基础巩固]
1.已知函数f(x)=x3的切线的斜率等于3,则切线有( )
A.1条 B.2条 C.3条 D.不确定
解析:选B ∵f′(x)=3x2=3,解得x=±1.切点有两个,即可得切线有2条.
2.曲线y=ex在点A(0,1)处的切线斜率为( )
A.1 B.2 C.e D.
解析:选A 由条件得y′=ex,根据导数的几何意义,可得k=y′| =e0=1.
x=0
3.曲线y=sin x在x=0处的切线的倾斜角是( )
A. B. C. D.
解析:选D 由题意知,y′=cos x,∴y′=cos 0=1.
设此切线的倾斜角为α,则tan α=1,
∵α∈[0,π),∴α=.
4.质点沿直线运动的路程s与时间t的关系是s=,则质点在t=4时的速度为( )
A. B.
C. D.
解析:选B ∵s′=t .∴当t=4时,
s′=×= .
5.直线y=x+b是曲线y=ln x(x>0)的一条切线,则实数b的值为( )
A.2 B.ln 2+1
C.ln 2-1 D.ln 2
解析:选C ∵y=ln x的导数y′=,∴令=,得x=2,∴切点为(2,ln 2).
代入直线y=x+b,得b=ln 2-1.
6.曲线y=ln x在点M(e,1)处的切线的斜率是________,切线方程为____________.
解析:∵y′=(ln x)′=,∴y′| =.
x=e
∴切线方程为y-1=(x-e),即x-ey=0.
答案: x-ey=0
7.与直线2x-y-4=0平行且与曲线y=ln x相切的直线方程是________.
解析:∵直线2x-y-4=0的斜率为k=2,
又∵y′=(ln x)′=,∴=2,解得x=.
∴切点的坐标为.
故切线方程为y+ln 2=2.
即2x-y-1-ln 2=0.
答案:2x-y-1-ln 2=0
8.设坐标平面上的抛物线C:y=x2,过第一象限的点(a,a2)作抛物线C的切线l,则直线l与y轴的交点
Q的坐标为________.
解析:显然点(a,a2)为抛物线C:y=x2上的点,
∵y′=2x,∴直线l的方程为y-a2=2a(x-a).
令x=0,得y=-a2,
∴直线l与y轴的交点的坐标为(0,-a2).
答案:(0,-a2)
9.求下列函数的导数.
(1)y=2;(2)y=;(3)y=10x;
(4)y=2cos2-1.
解:(1)∵y′=c′=0,∴y′=2′=0.(2)∵y′=(xα)′=n·xα-1,
∴y′=()′= ′=x =x = .
(3)∵y′=(ax)′=ax·ln a,
∴y′=(10x)′=10x·ln 10.
(4)∵y=2cos2-1=cos x,
∴y′=(cos x)′=-sin x.
10.已知P(-1,1),Q(2,4)是曲线y=x2 上的两点.
(1)求过点P,Q的曲线y=x2的切线方程;
(2)求与直线PQ平行的曲线y=x2的切线方程.
解:(1)因为y′=2x,P(-1,1),Q(2,4)都是曲线y=x2上的点.
过P点的切线的斜率k=y′| =-2,
1 x=-1
过Q点的切线的斜率k=y′| =4,
2 x=2
过P点的切线方程:y-1=-2(x+1),
即2x+y+1=0.
过Q点的切线方程:y-4=4(x-2),
即4x-y-4=0.
(2)因为y′=2x,
直线PQ的斜率k==1,
切线的斜率k=y′|x=x=2x=1,
0 0
所以x=,所以切点M,
0
与PQ平行的切线方程为:
y-=x-,即4x-4y-1=0.[B级 综合运用]
11.(多选)在曲线f(x)=上切线的倾斜角为π的点的坐标为( )
A.(1,1) B.(-1,-1)
C. D.
解析:选AB 因为f(x)=,所以f′(x)=-,因为切线的倾斜角为π,所以切线斜率为-1,
即f′(x)=-=-1,所以x=±1,
则当x=1时,f(1)=1;
当x=-1时,f(1)=-1,则点的坐标为(1,1)或(-1,-1).
12.设曲线y=xn+1(n∈N*)在点(1,1)处的切线与x轴的交点的横坐标为x ,则x·x·…·x 的值为( )
n 1 2 n
A. B.
C. D.1
解析:选B 对y=xn+1(n∈N*)求导得y′=(n+1)xn. 令x=1,得在点(1,1)处的切线的斜率k=n+1,∴在
点(1,1)处的切线方程为y-1=(n+1)(x-1).令y=0,得x =,∴x·x·…·x =×××…××=, 故选B.
n 1 2 n
13.若曲线y=在点P(a,)处的切线与两坐标轴围成的三角形的面积为2,则实数a的值是________.
解析:∵y′=,∴切线方程为y-=(x-a),令x=0,得y=,令y=0,得x=-a,由题意知··a=2,∴a=
4.
答案:4
14.已知曲线方程为y=f(x)=x2,求过点B(3,5)且与曲线相切的直线方程.
解:设切点P的坐标为(x,x).
0
∵y=x2,∴y′=2x,∴k=f′(x)=2x,
0 0
∴切线方程为y-x=2x(x-x).
0 0
将点B(3,5)代入上式,得5-x=2x(3-x),
0 0
即x-6x+5=0,∴(x-1)(x-5)=0,
0 0 0
∴x=1或x=5,
0 0∴切点坐标为(1,1)或(5,25),
故所求切线方程为y-1=2(x-1)或y-25=10(x-5),
即2x-y-1=0或10x-y-25=0.
[C级 拓展探究]
15.求证:双曲线xy=a2上任意一点处的切线与两坐标轴围成的三角形的面积等于常数.
证明:设P(x,y)为双曲线xy=a2上任一点.
0 0
∵y′=′=-.
∴过点P的切线方程为y-y=-(x-x).
0 0
令x=0,得y=;令y=0,得x=2x.
0
则切线与两坐标轴围成的三角形的面积为
S=··|2x|=2a2.
0
即双曲线xy=a2上任意一点处的切线与两坐标轴围成的三角形的面积为常数2a2.