文档内容
专题2.5 期中真题模拟卷05(1-3 章)
一.选择题(共12小题)
1.(2020·安徽省太和中学(文))已知 ,则“ ”是“ ”的( )
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分又非必要条件
【答案】A
【解析】
a∈R,则“a>1”⇒“ ”,
“ ”⇒“a>1或a<0”,
∴“a>1”是“ ”的充分非必要条件.
故选A.
2.(2020·四川)若a>b,则下列各式中正确的是( )
A.ac>bc B.ac2>bc2 C.a+c2>b+c2 D.
【答案】C
【解析】A. ac>bc, 时显然不成立;
B.ac2>bc2, 时,不成立;
C. a+c2>b+c2,利用不等式的加法法则可以证明是正确的;
D. ,符号不能确定,是错误的.
故选C
3.(2020·怀仁市第一中学校月考(文))设 , ,
,则 , , 的大小顺序为( )
A. B. C. D.
【答案】D
【解析】
、 、 的大小顺序是 .
故选: .
4.(2020·沭阳县修远中学月考)已知 ,且 , 恒
成立,则实数 的取值围是( )
A. B.C. D.
【答案】C
【解析】
依题意 ,
当 等号成立,故 恒成,化简得 ,解得
,
故选:C.
5.(2020·安徽金安六安一中(文))若函数 在 处取最
小值,则 ( )
A. B.2 C.4 D.6
【答案】C
【解析】
由题意, ,而
,当且仅当 ,即 时,等号成立,
所以 .
故选:C.6.(2020·江西省信丰中学月考)已知关于 的不等式 的解集是
,则 等于( )
A.2 B. C. D.
【答案】B
【解析】
根据题意,关于 的不等式 的解集是 ,
则方程 的两根为 与 ,且 ,
故可得 ,解可得: ,
故选:B.
7.(2019·黑龙江哈师大青冈实验中学月考(理))已知命题“∃x
0
∈R,
”是假命题,则实数a的取值范围为( )
A.(-∞,0) B.[0,4]
C.[4,+∞) D.(0,4)
【答案】D
【解析】因为命题“∃x
0
∈R, ”是假命题,
所以其否定“∀x∈R, ”是真命题,
则 ,解得 .
故选:D.
8.(2020·湖南宁远(理))将函数 的图象向左平移1个单位长度,得到
函数 的图象,则函数 的图象大致是( )
A. B. C. D.
【答案】B
【解析】
.
因为 ,
即 ,所以 为奇函数,排除A;
令 ,解得 ,即 有唯-的零点 ,排除C;由解析式可知 ,排除D.
只有B符合条件.
故选:B.
9.(2020·永安市第三中学月考)如果 在区间 上为减函
数,则 的取值( )
A. B. C. D.
【答案】C
【解析】
解:由题意,当 时,可得 ,在 上是单调递减,满足题意;
当 时,显然不成立;
当 时,要使 在 上为减函数,
则 ,解得: ,∴ ;
综上: ,
故选:C.
10.(2019·永济中学月考)已知定义在R上的奇函数 ,当 时,
,若对任意实数x有 成立,则正数 的取值范围为()
A. B. C. D.
【答案】C
【解析】
由题得, 当 时, ,故写成分段函数
,化简得 ,又 为奇函数,故可画出图像:
又 可看出 往右平移 个单位可得,若 恒成立,则
,即 ,又 为正数,故解得 .
故选C.
11.(2019·全国)已知 ,若 ,则 =
( )
A. B.2 C.4 D.1【答案】C
【解析】
因为
所以
因而
所以
所以选C
12.(2020·浙江省宁海中学月考)已知 ,不等式 在 上恒成
立,则( )
A. B. C. D.
【答案】D
【解析】
解:∵ ,且 ,
∴ ,
∴ ,∴ ,
∵上述不等式恒成立,
∴ ,即 (否则取 ,则左边 ,矛盾),
此时不等式转化为 ,
∴ ,解得 ,
∴ ,
故选:D.
二.填空题(共6小题)
13.(2020·上海市七宝中学期末)不等式 对任意 恒成立的充要条
件是 __________.
【答案】
【解析】
解:当 时,显然满足条件,
当 时,由一元二次不等式恒成立得: ,解得:
综上, ,
所以不等式 对任意 恒成立的充要条件是 ,故答案为:
14.(2020·武汉市钢城第四中学月考)已知 , ,则 的取
值范围是______
【答案】
【解析】
解:令
则 ,
,
又 ,①
,
②
① ②得 .
故答案为:
15.(2020·沙坪坝·重庆一中月考(理))已知 , 且 ,则 的
最小值为____________.【答案】 .
【解析】
由 可得:
,则:
,
故答案为: .
16.(2020·辽宁沙河口·辽师大附中期末)已知二次不等式 的解集为
,且 ,则 的最小值为__________.
【答案】
【解析】
由于二次不等式 的解集为 ,
则 , 且 , , .
.当且仅当 时,等号成立.
因此, 的最小值为 .
故答案为 .
17.(2020·安徽黄山期中)当 时,则 的值域是____________
【答案】
【解析】
因为 ,且 ,
①当 时, ,
所以 ,
当且仅当 ,即 时,取“ ”.
②当 时, , ,
所以 ,因为 ,
所以 ,即 .
当且仅当 ,即 时,取“ ”.
综上所述值域为: .
故答案为:
18.(2020·全国)若不等式组 的整数解只有-2,则k的取值范
围是________.
【答案】
【解析】
不等式 的解集为 ,
不等式 可转化为: ,
根据已知条件不等式组的整数解只有 ,
不等式 的解集为 ,
再借助数轴可得 的取值范围为 ,解得 ,综上k的取值范围是 ,故答案为 .
三.解析题(共6小题)
19.(2020·浙江)已知集合 ,集合 .
(1)求 ;
(2)设集合 ,且 ,求实数 的取值范围.
【答案】(1) (2)
【解析】
(1) 集合 .
则
集合 ,
则
(2) 集合 ,且
,解得
故实数 的取值范围为
20.(2020·沙坪坝·重庆南开中学月考(文))已知 , .(1)若 ,求 的最小值;
(2)求证 .
【答案】(1)9;(2)证明见解析.
【解析】
(1)因为 , ,
所以 ,
当且仅当: , 时取最小值9.
(2)因为 , ,
要证 ,只需证 ,
而 .
,
当且仅当“ ”时取等号.
即证: .21.(2020·柴河林业局第一中学月考)已知函数 .
(1)若关于x的不等式 的解集是 ,求实数 的值;
(2)若 ,解关于x的不等式 .
【答案】(1) (2) 时 , 时
【解析】
(1)由题 ,3是方程 的二根.
代入有 ,∴
(2)
∵ ∴
①当
②
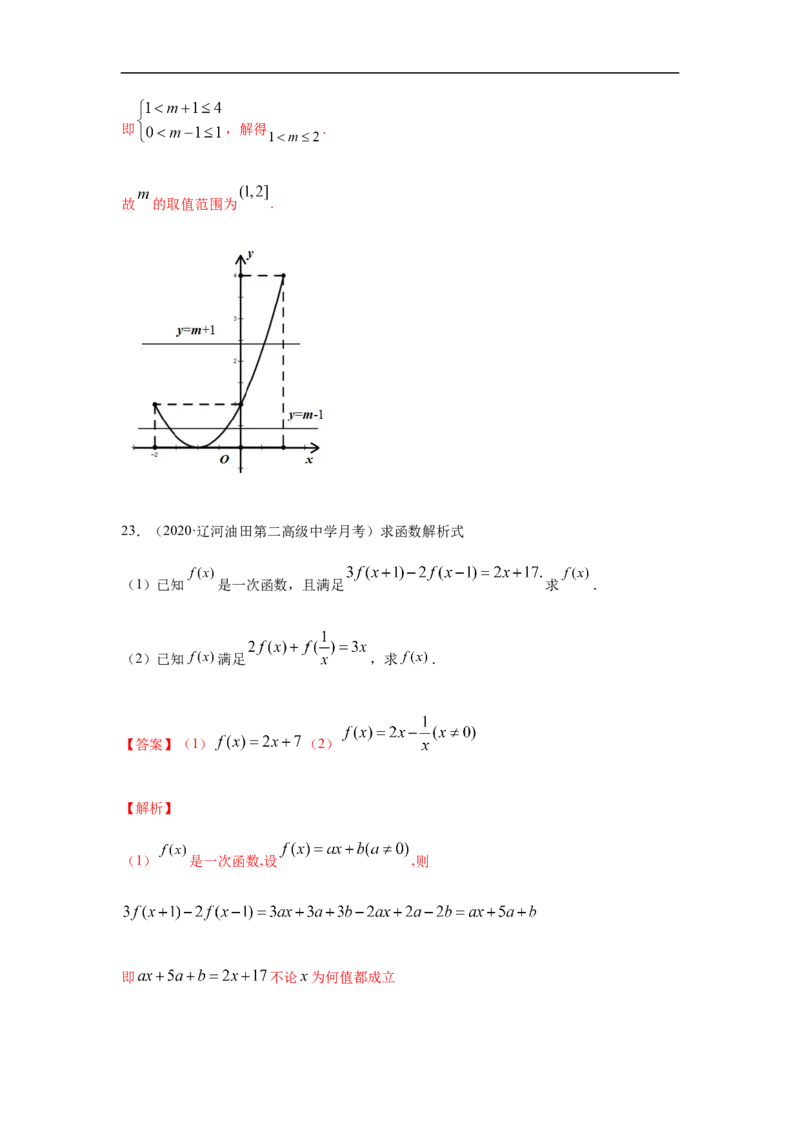
22.(2020·四川阆中中学(文))已知函数 .(1)若 的值域为 ,求关于 的方程 的解;
(2)当 时,函数 在 上有三个零点,求 的
取值范围.
【答案】(1) 或 ;(2) .
【解析】
(1)因为 的值域为 ,所以 .
因为 ,所以 ,则 .
因为 ,所以 ,即 ,
解得 或 ;
(2) 在 上有三个零点等价于方程
在 上有三个不同的根.
因为 ,所以 或 .
因为 ,所以 .
结合 在 上的图像可知,要使方程 在 上有
三个不同的根,则 在 上有一个实数根, 在 上有两
个不等实数根,即 ,解得 .
故 的取值范围为 .
23.(2020·辽河油田第二高级中学月考)求函数解析式
(1)已知 是一次函数,且满足 求 .
(2)已知 满足 ,求 .
【答案】(1) (2)
【解析】
(1) 是一次函数,设 ,则
即 不论 为何值都成立所以 解得
故 的解析式为
(2) ∵ ①
∴ ②
① ②-②得 ,
故
24.(2019·贵州凤冈月考)定义在非零实数集上的函数 对任意非零实数 满足:
,且当 时 .
(1)求 及 的值;
(2)求证: 是偶函数;
(3)解不等式: .
【答案】(1)f(-1)=0,f(1)=0;(2)见解析;(3)
【解析】(1)在 中,令 ,可得 ,解得 .
令 ,可得: ,解得: .
(2) 中,令 ,可得 ,
所以函数 是偶函数.
(3)当 时, ,由题意得:
,
所以 在 上是增函数,
又由(2)知 是偶函数,
所以 等价于 ,等价于 ,
又 在 上是增函数,所以 ,且 ,
解得: 且 ,
所以不等式的解集为