文档内容
专题4. 5数学归纳法(A卷基础篇)(人教A版第二册,浙江专用)
参考答案与试题解析
第Ⅰ卷(选择题)
一.选择题(共10小题,满分50分,每小题5分)
1.(2020·吉林吉林市·高二期末(理))用数学归纳法证明等式, 时,由
到 时,等式左边应添加的项是( )
A. B.
C. D.
【答案】C
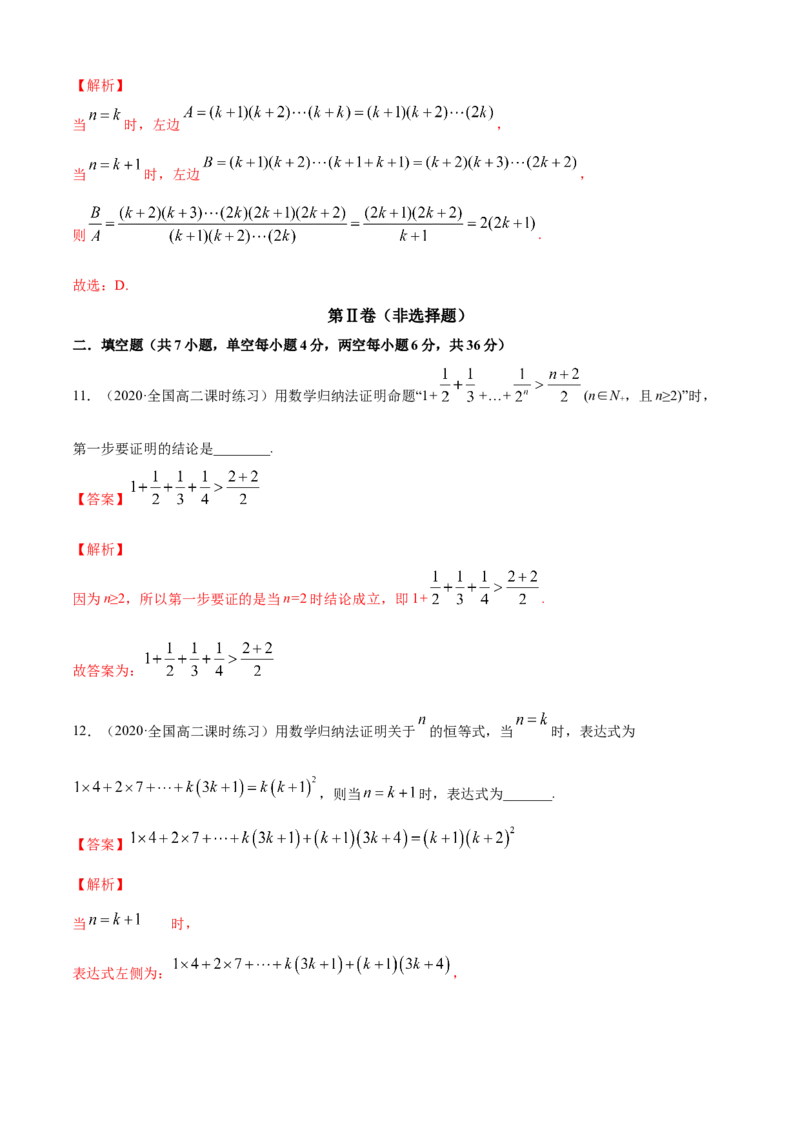
【解析】
因为要证明等式的左边是连续正整数,所以当由 到 时,等式左边增加了
,故选C.
2.(2020·全国高二课时练习)用数学归纳法证明 时,第一步应
验证的不等式是( )
A. B.
C. D.
【答案】B
【解析】
∵ , ,
∴ 所取的第一个正整数为2,又 ,故第一步应验证 .
故选:B
3.(2020·上海市新场中学高二月考)用数学归纳法证明等式
时,当 时,左边等于( )
A.1 B. C. D.
【答案】C
【解析】
用数学归纳法证明: ,
在验证 时,
令 代入左边的代数式,得到左边 .
故选:C
4.(2020·陕西宝鸡市·高二期末(理))用数学归纳法证明 ,则当
时,左端应在 的基础上加上( )
A. B.
C. D.
【答案】C
【解析】
当 时,等式左端 ,
当 时,等式左端 ,增加了项 .
故选:C.
5.(2020·上海浦东新区·华师大二附中高一期末)用数学归纳法证明
, 成立.那么,“当 时,命题成立”是“对 时,
命题成立”的( )
A.充分不必要 B.必要不充分 C.充要 D.既不充分也不必要
【答案】B
【解析】
“当 时,命题成立”不能推出“对 时,命题成立”,
“对 时,命题成立”可以推出“当 时,命题成立”,
所以“当 时,命题成立”是“对 时,命题成立”的必要不充分/
故选:B
6.(2020·吉林白城市·白城一中高二期末(理))用数学归纳法证明 时,从
到 ,不等式左边需添加的项是( )
A. B.
C. D.
【答案】B
【解析】
当 时,所假设的不等式为 ,
当 时,要证明的不等式为 ,故需添加的项为: ,
故选:B.
7.(2020·全国高三专题练习)用数学归纳法证明不等式 的过程中,由
递推到 时,不等式左边( )
A.增加了一项
B.增加了两项 ,
C.增加了A中的一项,但又减少了另一项
D.增加了B中的两项,但又减少了另一项
【答案】D
【解析】
当 时,左边 ,
当 时,左边
,
所以,由 递推到 时,不等式左边增加了 , ;减少了 ;
故选D
8.(2020·梧州高级中学高二期中(理))已知n为正偶数,用数学归纳法证明时,若已假设 为偶数)时命题为真,则
还需要用归纳假设再证 ( )时等式成立( )
A. B. C. D.
【答案】B
【解析】
若已假设n=k(k≥2,k为偶数)时命题为真,因为n只能取偶数,所以还需要证明n=k+2成立.、
故选B.
9.(2020·上海高二课时练习)用数学归纳法证明命题“当n为奇数时, 能被 整除”,在证明
正确后,归纳假设应写成( ).
A.假设 时命题成立
B.假设 时命题成立
C.假设 时命题成立
D.假设 时命题成立
【答案】D
【解析】
此题所成立的数是所有的正奇数,根据数学归纳法的证题步骤要求,第二步所取的值的范围应从 开
始取值所有奇数,即 .
故选:D.
10.(2020·上海高二课时练习)在用数学归纳法求证: 的
过程中, 从“ 到 ”左边需增乘的代数式为( ).
A. B. C. D.
【答案】D【解析】
当 时,左边 ,
当 时,左边 ,
则 .
故选:D.
第Ⅱ卷(非选择题)
二.填空题(共7小题,单空每小题4分,两空每小题6分,共36分)
11.(2020·全国高二课时练习)用数学归纳法证明命题“1+ +…+ (n∈N ,且n≥2)”时,
+
第一步要证明的结论是________.
【答案】
【解析】
因为n≥2,所以第一步要证的是当n=2时结论成立,即1+ .
故答案为:
12.(2020·全国高二课时练习)用数学归纳法证明关于 的恒等式,当 时,表达式为
,则当 时,表达式为_______.
【答案】
【解析】
当 时,
表达式左侧为: ,表达式右侧为: ,
则当 时,表达式为 .
故答案为: .
13.(2020·全国高二课时练习)用数学归纳法证明
时,第一步应验证的等式是________.
【答案】
【解析】
由题知等式的左边有 项,右边有 项,且 ,因此第一步应验证 时的等式,此时左边
,右边 ,
故答案为: .
14.(2020·浙江高三其他模拟)用数学归纳法证明:
,第一步应验证的等式是__________;从“
”到“ ”左边需增加的等式是_________.
【答案】
【解析】
当 时,应当验证的第一个式子是 ,从“ ”到“ ”左边需增加的式子是15.(2020·上海高二课时练习)用数学归纳法证明:“对任意奇数n,命题 成立”时,第二步论证
应该是假设 ______命题成立,再证 ______时,命题也成立.
【答案】
【解析】
依题意用数学归纳法证明:“对任意奇数n,命题 成立”,由于 为奇数,所以第二步论证应该是假
设 命题成立,再证 时命题也成立.
故答案为: ;
16.(2018·浙江宁波市·余姚中学高二期中)已知 为正偶数,用数学归纳法证明“
”时,第一步的验证为
________________________;若已假设 ( 且 为偶数)时等式成立,则还需要用归纳假设证
________时等式成立.
【答案】当 时,左边 ,右边 ,等式成立;
【解析】
对 在 为正偶数,用数学归纳法证明
归纳基础,因为 为正偶数,则基础 ,
当 时,左边 ,右边 ,等式成立;
归纳假设,当 ( 且 为偶数)时,成立
由于是所有正偶数,则归纳推广,应到下一个数为 时,等式成立
故答案为:(1). 当 时,左边 ,右边 ,等式成立; (2).
17.(2020·江苏苏州市·高二期中)在数列 中,a=1, ,则a=______,
1 3
a=_______.
n
【答案】
【解析】
第一空:因为 , ,所以 , ;
第二空:由第一空可知: ,所以可得 ,
因为 , , ,
,所以猜想 ,数学归纳法证明如下:
(1)当 时,显然 ;
(2)假设当 时成立,即 ,
当 时,综合(1)(2),所以 ,
故答案为: ;
三.解答题(共5小题,满分64分,18--20每小题12分,21,22每小题14分)
18.(2020·上海高二课时练习)在证明 ,由
到 的变化过程中,左边增加的部分是什么,右边增加的部分是什么?
【答案】 ;
【解析】
时,左边为 ,
时,变为 ,
故由 到 的变化过程中,左边增加的都分是 ;时,右边为 ,
时,变为 ,
右边增加的部分是 .
故答案为: ; .
19.(2020·上海高二课时练习)用数学归纳法证明:对任意正整数 能被9整除.
【答案】见解析
【解析】
证明:(1)当 时, ,能被9整除,
故当 时, 能被9整除.
(2)假设当 时,命题成立,即 能被9整除,
则当 时, 也能被9整除.
综合(1)(2)可得, 对任意正整数 能被9整除.
20.(2020·旬邑县中学高二月考(理))已知数列 满足 , .
(1)求 、 ;
(2)猜想数列通项公式 ,并用数学归纳法给出证明.
【答案】(1) , ;(2) ,证明见解析.
【解析】(1) , ;
(2)猜想数列通项公式 ,证明如下:
当 时, , ,所以 成立;
假设 时成立,即 ,
当 时, ,
∴ 时, 成立,
综上,由①②得: .
21.(2016·广东揭阳市·高二月考)设数列 的前 项和为 ,并且满足 .猜
想 的通项公式,并用数学归纳法加以证明.
【答案】
【解析】
(1)解:分别令 ,得 ,
∵ ,∴ ,猜想: ,由 ①
可知,当 时 ②
①-②得 ,即当 时
∵ ,∴ ,
(ii)假设当 时, ,那么当 时,
,∵ ,
∴ ,∴ ,即当 时也成立.
∴ ,显然 时,也成立,故对于一切 ,均有 .
22.(2016·广西桂林市·高二期中)在数列{a}中,a=1且
n 1
(1)求出 , , ;
(2)归纳出数列{a}的通项公式,并用数学归纳法证明归纳出的结论.
n
【答案】(1) , , ;(2) .
【解析】
(1)由a=1且 知:
1
, ,
(2)猜想数列 的通项公式为 ,证明如下:
(i)当n=1时,左边= ,右边= 左边=右边 即猜想成立;
(ii)假设当n= 时,猜想成立,即有
那么当n= 时,从而猜想对n= 也成立;
由(i)(ii)可知,猜想对任意的 都成立,所以数列 的通项公式为