文档内容
专题5. 4《一元函数的导数及其应用》单元测试卷(A卷基础篇)
(新教材人教A版,浙江专用)
参考答案与试题解析
第Ⅰ卷(选择题)
一.选择题(共10小题,满分50分,每小题5分)
1.(2020·全国高二课时练习)已知函数 ,则 ( )
A. B. C. D.
【答案】D
【解析】
, ,因此, .
故选:D.
2.(2020·河北高三月考)函数 的图象在点 处的切线斜率为( )
A.2 B.-2 C.4 D.
【答案】D
【解析】
因为 ,所以 , .
故选:D
3.(2020·云南昆明市·昆明一中高三其他模拟(理))函数 的单调递减区间是(
)
A. B. C. D.
【答案】D【解析】
函数的定义域是 , ,
令 ,解得 ,
故函数 在 上单调递减,
选:D.
4.(2020·北京朝阳区·高二期末)曲线 在点 处的切线方程为( )
A. B. C. D.
【答案】A
【解析】
, ,根据导数的几何意义可知曲线在 处的切线的斜率 ,所以曲线
在点 处的切线方程为 ,即 .
故选:A
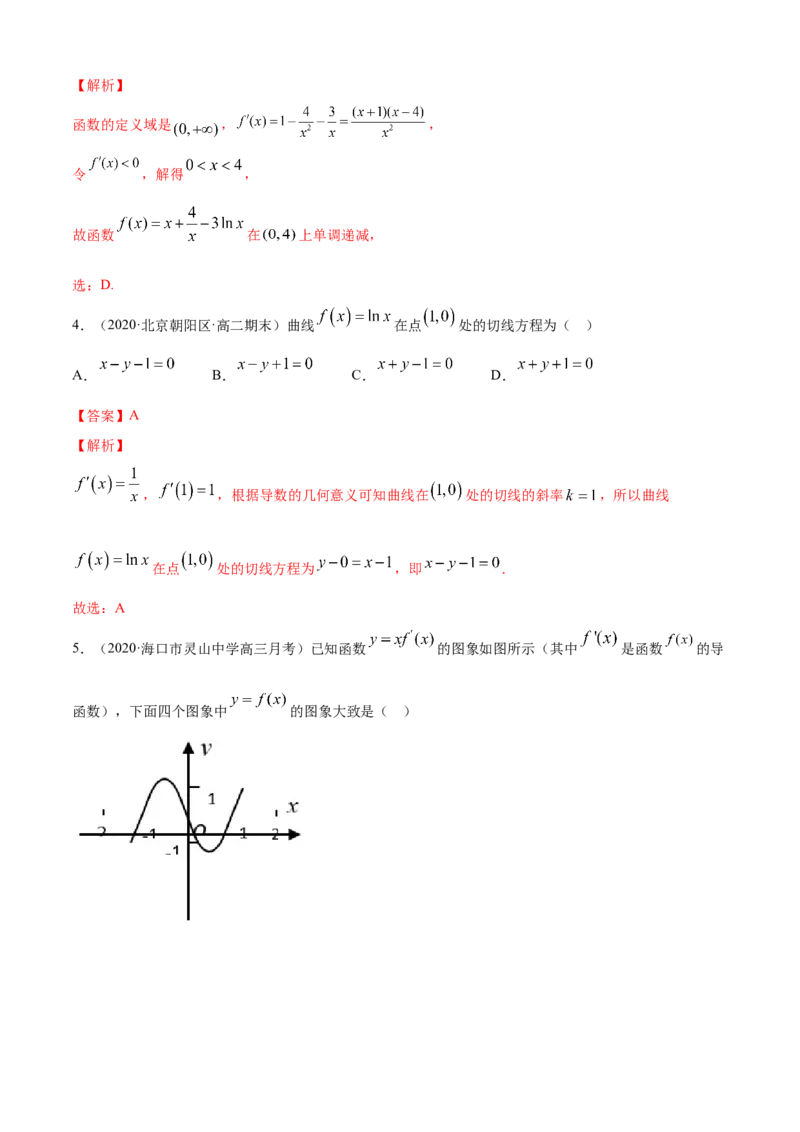
5.(2020·海口市灵山中学高三月考)已知函数 的图象如图所示(其中 是函数 的导
函数),下面四个图象中 的图象大致是( )A. B.
C. D.
【答案】C
【解析】
由函数 的图象可知:
当 时, , ,此时 单调递增;
当 时, , ,此时 单调递减;
当 时, , ,此时 单调递减;
当 时, , ,此时 单调递增.
故选:C
6.(2020·厦门市湖滨中学高三月考)已知函数 在区间 上单调递增,则 的取值
范围是( )
A. B. C. D.
【答案】A
【解析】在区间 上恒成立,则 在区间 上恒成立
即
故选:A
7.(2020·洛阳市第一高级中学高三月考(文))已知函数 的导函数为 ,且满足关系式
,则 的值等于( )
A. B. C. D.
【答案】D
【解析】
依题意 ,令 得 , ,故选D.
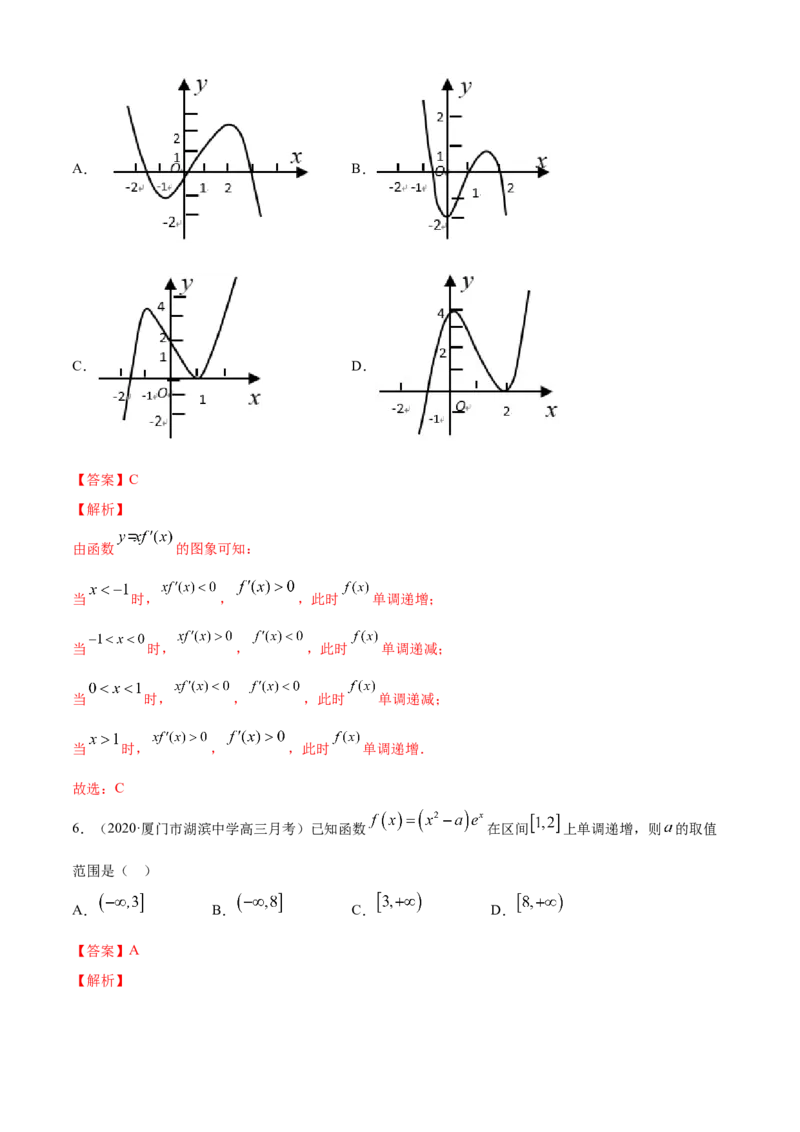
8.(2020·全国高三专题练习(文))已知函数f(x)的图象如图所示,下列数值的排序正确的是( )
A. B.
C. D.
【答案】B
【解析】由图可知: ,
即 .
故选:B
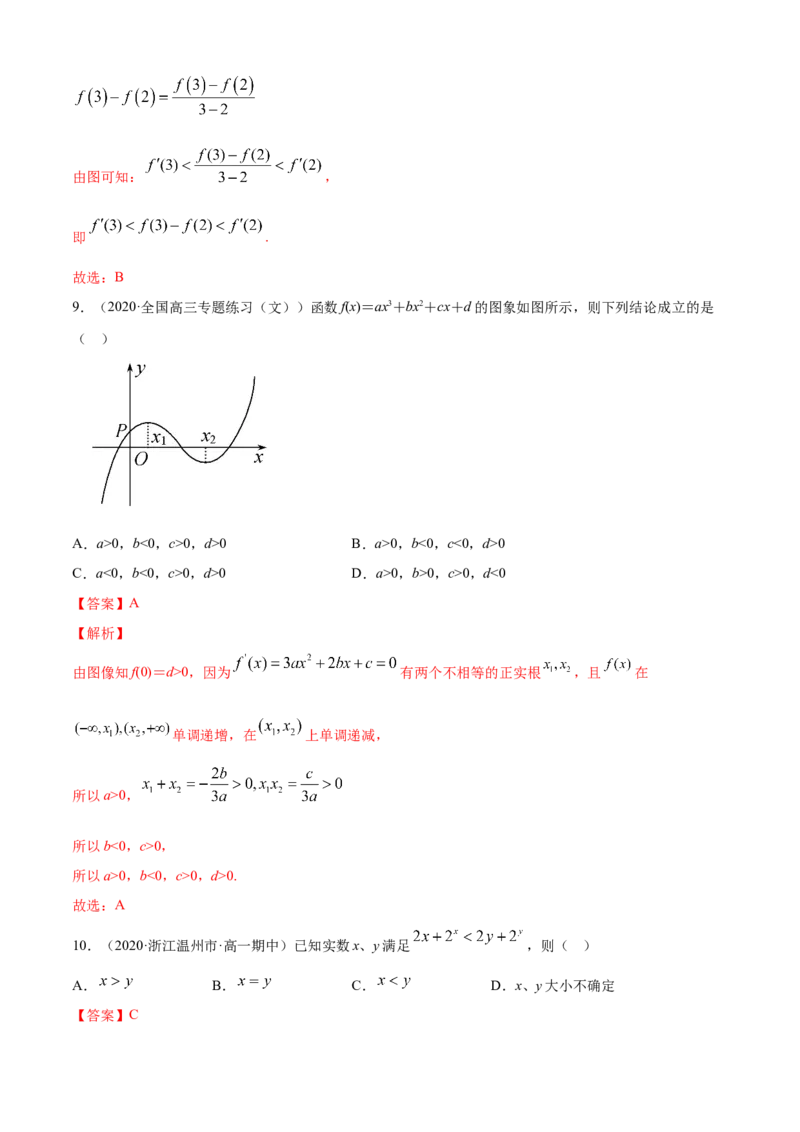
9.(2020·全国高三专题练习(文))函数f(x)=ax3+bx2+cx+d的图象如图所示,则下列结论成立的是
( )
A.a>0,b<0,c>0,d>0 B.a>0,b<0,c<0,d>0
C.a<0,b<0,c>0,d>0 D.a>0,b>0,c>0,d<0
【答案】A
【解析】
由图像知f(0)=d>0,因为 有两个不相等的正实根 ,且 在
单调递增,在 上单调递减,
所以a>0,
所以b<0,c>0,
所以a>0,b<0,c>0,d>0.
故选:A
10.(2020·浙江温州市·高一期中)已知实数x、y满足 ,则( )
A. B. C. D.x、y大小不确定
【答案】C【解析】
设 ,
所以 ,
所以函数 在 上单调递增,
由题得 ,
所以 .
故选:C
第Ⅱ卷(非选择题)
二.填空题(共7小题,单空每小题4分,两空每小题6分,共36分)
11.(2020·全国高二课时练习)若函数 在 内是增函数,则实数b的取值范围是
_________.
【答案】
【解析】
由题意得 在 内恒成立,
即 在 内恒成立,
所以 .
故答案为:
12.(2020·海口市第四中学高三期中)若函数 在 处取得极值,则 ________.
【答案】
【解析】
由题意,函数 ,可得 ,
因为 是函数 的极值点,可得 ,
所以 ,解得 .故答案为: .
13.(2020·湖南长沙市·雅礼中学高二期中)曲线 的一条切线的斜率为2,则切点坐标为
_________.
【答案】
【解析】
由 ,得 ,
设切点坐标为 , ,
则 ,解得 ,
.
则切点坐标为 .
故答案为: .
14.(2018·全国高二课时练习)把长为60m的铁丝围成矩形,当长为___m,宽为___m时,矩形的面积最大.
【答案】15 15
【解析】
设矩形的长为xm,则宽为(30-x)m,
矩形面积S=30x-x2(0