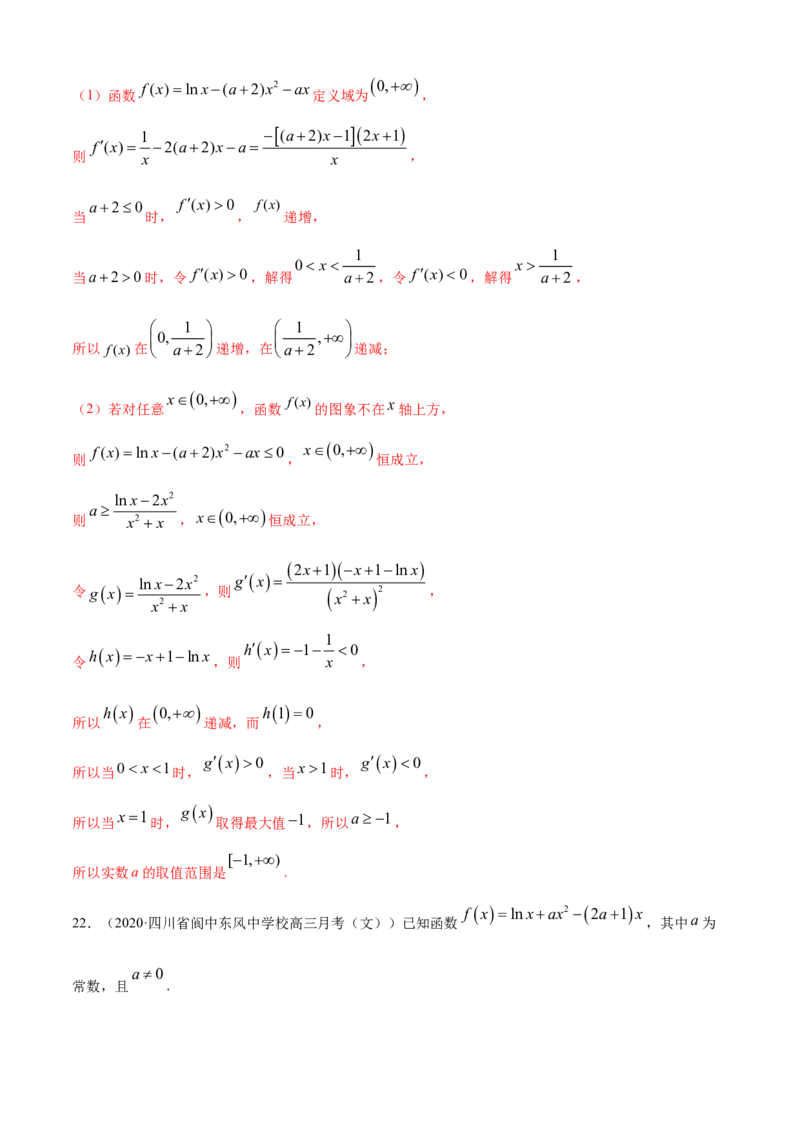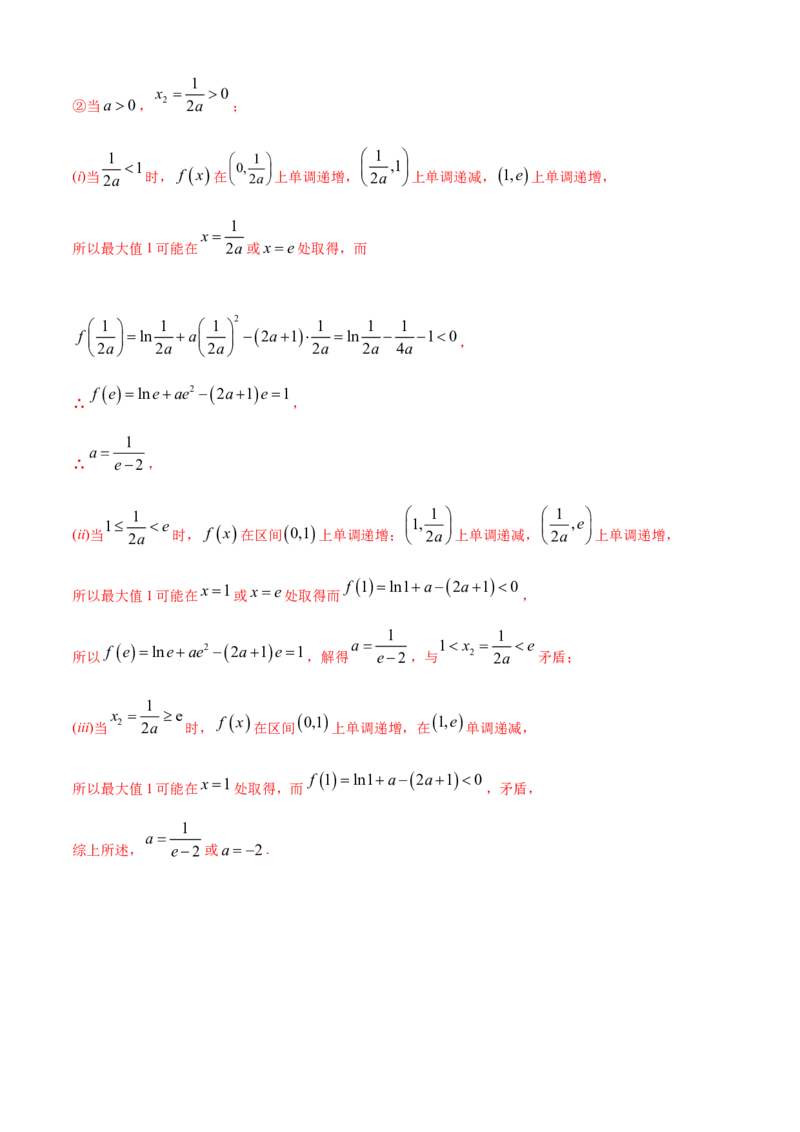专题5.4《一元函数的导数及其应用》单元测试卷（B卷提升篇）解析版_E015高中全科试卷_数学试题_选修2_01.同步练习_同步练习（第四套）

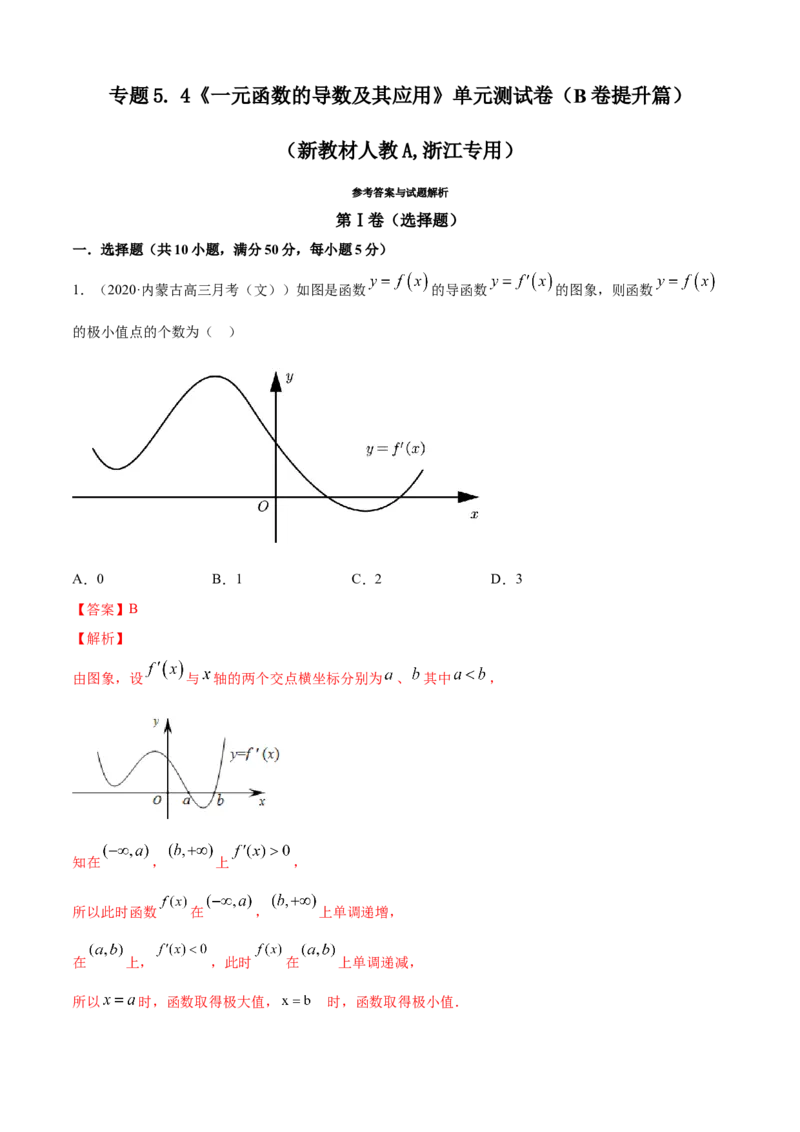
专题5. 4《一元函数的导数及其应用》单元测试卷（B 卷提升篇） （新教材人教A,浙江专用） 参考答案与试题解析 第Ⅰ卷（选择题） 一．选择题（共10小题，满分50分，每小题5分） 1．（2020·内蒙古高三月考（文））如图是函数 的导函数 的图象，则函数 的极小值点的个数为（ ） A．0 B．1 C．2 D．3 【答案】B 【解析】 由图象，设 与 轴的两个交点横坐标分别为 、 其中 ， 知在 ， 上 ， 所以此时函数 在 ， 上单调递增， 在 上， ，此时 在 上单调递减， 所以 时，函数取得极大值， 时，函数取得极小值．则函数 的极小值点的个数为1． 故选: B f x gx f xxgx x2 1 f 11 2．（2020·湖南长郡中学高二期中）若函数 ， 满足 ，且 ，则 f1g1 （ ） A．1 B．2 C．3 D．4 【答案】C 【解析】 f x gx f xxgx x2 1 f 11 因为函数 ， 满足 ，且 ， f 1g112 10 g11 所以 ，则 ， f xxgx x2 1 对 两边求导， fxgxxgx2x 可得 ， f1g1g12 f1g13 所以 ，因此 . 故选：C. {a } a 2 a 4 3.（2020·安徽淮北一中高二期中）等比数列 n 中， 1 ， 8 ，函数 f(x) x(xa )(xa )…(xa ) f(0)( 1 2 8 ，则 （ ） A．26 B．29 C．212 D．215 【答案】C 【解析】 {a } a 2 a 4 等比数列 n 中， 1 ， 8 ， aa a a a a a a 248 所以 1 8 2 7 3 6 4 5 ， f(x)x(xa )(xa )(xa ) 因为函数 1 2 8 ， f(x)(xa )(xa )(xa )x(xa )(xa )(xa ) 1 2 8 1 2 8 ，f(0)aa a (aa )4 84 212 则 1 2 8 1 8 ． 故选：C． f(x) x3 12x16 4．（2020·天津经济技术开发区第二中学高三期中）函数 的零点个数为（ ） 0 1 2 3 A． B． C． D． 【答案】C 【解析】 f(x)3x2 123(x2)(x2) 由题得 ， f(x)0 x2 x2 f(x)0 2 x2 令 得 或 ，令 得 ， (,2),(2,) (2,2) 所以函数的单调递增区间为 ，减区间为 . f(2)0 f(2)32 所以函数的极大值为 ，极小值为 ， x y0, x y 0, 当 时， 当 时， 所以函数的零点个数为2. 故选：C 5.（2020·辽宁高三月考）点 是曲线 上任意一点，曲线在点 处的切线与 平行，则 的横坐标为（ ） A．1 B． C． D． 【答案】A 【解析】 由题意，设 ， ， 由 得 ，则 ， 因为曲线在点 处的切线与 平行，所以 ，解得： 或 （舍） 故选：A. 6．（2020·宁夏银川一中高三月考（文））若函数 在 上单调递减，则实数 的取值范围是（ ） A． B． C． D． 【答案】C 【解析】 由题意可得： 在 上恒成立， 整理可得： ， 函数 在 上递减， 所以 ， 所以 ， 故选：C. f x2axasinxcosx 7．（2020·湖北高三月考）若函数 是R上的增函数，则实数 a 的取值范围是 （ ）  3  3  A．   , 3  B．  3 ,  C． , 3  D． 3,      【答案】B 【解析】 f x2axasinxcosx 因为 ， f(x)2aacosxsinx a2 1sin(x)2a,tana 所以f(x) R 因为 在 上的增函数， f(x)0 所以 在R上恒成立， 所以 f(x) min  a2 12a0 ，即2a a2 1， a0 3  a 所以 4a2 a2 1，解得 3 ， 故选：B f(x)exbax a,bR f(0)1 x0 8．（2020·全国高三专题练习（理））已知函数 ，且 ，当 时， f(x)xcos(x1) 恒成立，则a的取值范围为（ ） (0,) (1e,) A． B． (,e) (e,) C． D． 【答案】B 【解析】 f(0)eb 1 b0 f(x)ex ax 由题意， ，解得 ，则 ， ex a cos(x1) 则当x0时，ex ax xcos(x1)，即 x 恒成立， ex ex(x1) s(x) ,x(0,) s(x) 令 x ，则 x2 ， x(0,1) s(x)0 x(1,) s(x)0 当 时， ， 时， ， s(x) (0,1) (1,) s(x) s(1)e 所以 在 上是减函数，在 是增函数， min ， x1 cos(x1) 又因为当 时， 取得最大值1， ex cos(x1) 所以当x1时， x 取得最大值1e，a 1e 所以 . 故选：B. f xex ax1b 0,1 9．（2020·江西高三其他模拟（理））设函数 在区间 上存在零点，则 a2 b2 的最小值为（ ） e e2 3e A．7 B． C． D． 【答案】C 【解析】 f xex ax1b 由题意，函数 ， f x 0,1 et at1b0 t 设 为函数 在 上的零点，则 ， t1abet 0 t1x yet 0 (a,b) 即 ，即点 在直线 上， a2 b2 (a,b) 又由 表示点 到原点的距离的平方， et 则 a2 b2  ，即a2 b2  e2t ， (t1)2 12 (t1)2 12 e2t 2e2t(t2 2t2)e2t(2t2) 2e2t(t2 3t3) gt gt  令 (t1)2 12 ，则 (t2 2t2)2 (t2 2t2)2 ， e2t 0,t2 3t30 gt0 因为 ，所以 ， gt t0,1 可得函数 在区间 上单调递增， g1e2 t 1 所以当 时，函数取得最大值，最大值为 ， a2 b2 e2 所以 的最小值为 . 故选：C. a,b e 10．（2020·浙江绍兴·高三月考）已知 为自然对数的底数， 为实数，且不等式b2 lnx(2ea1)xb10对任意的x(0,)恒成立.则当 a1取最大值时，a的值为（ ） 2e 2e1 3e 3e1 A． B． C． D． 【答案】D 【解析】 1 f xlnx(2ea1)xb1 fx 2ea1 设 ，则 x ， fx0 f x 0, a2e1 当 时， ，所以 在 上递增，不符合条件， 1 fx0 x 故a2e1，令 得 a12e ，  1   1  0, , 所以 f x 在   a12e  上递增，  a12e  上递增，  1  1 f x  f ln b0 故有 max  a12e   a12e ，即blna12e ， b2 lna12e2  则有 a1 a1 ， t lnt2e2 lnt2e2 令 t a1,t 2e ， gt t ，则 gt t2e t 在 2e, 上递减，且 b2 g3e0 gt 2e,3e 3e, gt g3e ，所以 在 上递增， 上递减，所以 ，此时 a1取得最大值， a13e a 3e1 且 ，所以 . 故选：D 第Ⅱ卷（非选择题） 二．填空题（共7小题，单空每小题4分，两空每小题6分，共36分） 11．（2020·湖北高三月考）函数 ，在点 处的切线方程为__________.【答案】 【解析】 ， 在点 处的切线方程为 ，即 故答案为： 12．（2020·全国高二课时练习）某批发商以每吨20元的价格购进一批建筑材料，若以每吨M元零售，销 量N（单位：吨）与零售价M（单位：元）有如下关系： ，则该批材料零售价定 为_______元时利润最大，利润的最大值为_________元. 【答案】30 23000 【解析】 设该商品的利润为y元， 由题意知， ， 则 ， 令 ，得 或 （舍去）， 当 时， ，当 时， ， 因此当 时，y取得极大值，也是最大值，且 . 故答案为：30，23000 13．（2020·天津经济技术开发区第二中学高三期中）已知函数 ，当 时， 函数 有极值，则函数 在 上的最大值为_________. 【答案】13 【解析】，当 时，函数 有极值， ，解得 ， ， 当 时， ， 单调递增， 当 时， ， 单调递减， 当 时， ， 单调递增， 在 处取得极大值 ， 且 ， ， 在 上的最大值为13. 故答案为：13. 14．（2020·全国高三专题练习）已知函数 ，设x=1是 的极值点，则a=___， 的单调增区间为___. 【答案】 【解析】 由题意可得： 是 的极值点即 令 ，可得 的单调递增区间为 15.（2020·全国高二单元测试）已知函数 ，对任意的 ，当 时， ，则实数a的取值范围是________． 【答案】 . 【解析】 由题意，分式 的几何意义为： 表示点 与 连线的斜率， 因为实数 在区间 内，故 和 在区间 内， 不等式 恒成立， 所以函数图象上在区间 内任意两点连线的斜率大于1， 故函数 的导数大于1在 内恒成立， 由函数 满足 ，即定义域为 ， 即 在 内恒成立，即 在 内恒成立， 设函数 ，根据二次函数的性质， 可得函数 在 上是单调增函数，可得 ，所以 ， 即实数 的取值范围是 . 16．（2020·辽宁高三月考）已知函数 有两个不同的极值点 ， ，则a的取值范 围___________；且不等式 恒成立，则实数 的取值范围___________. 【答案】 【解析】 ， 因为函数 有两个不同的极值点 , 所以方程 有两个不相等的正实数根， 于是有： ，解得 . , 设 , ，故 在 上单调递增，故 ，所以 . 因此 的取值范围是 故答案为： ； 17．（2020·湖北荆州市·高二期末）已知函数 ．（1）当 时， 的极小 值为________；（2）若 在 上恒成立，则实数a的取值范围为___________． 【答案】1 【解析】 （1） 时， ， ， ， ， 故 在 单调递增，而 （1） ， 故 时， ， 单调递减， 时， ， 单调递增， 故 极小值 （1） ； （2）若 在 上恒成立，即 在 恒成立， ① 即 时， ， ， ， 故 在 恒成立，② 即 时，即为 在 恒成立， 即 ，只需求出 的最大值即可， ， ，令 ，解得： ，令 ，解得： ， 故 在 单调递增，在 ， 单调递减， 故 ， 故 ， 综上， ， ． 故答案为：1， ， ． 三．解答题（共5小题，满分64分，18--20每小题12分，21,22每小题14分） 18．（2020·南通西藏民族中学高二期中）已知函数f(x)＝x＋ ，g(x)＝2x＋a. （1）求函数f(x)＝x＋ 在 上的值域； （2）若 x∈ ， x∈[2，3]，使得f(x)≥g(x)，求实数a的取值范围. 1 2 1 2 ∀ ∃ 【答案】（1） ；（2） . 【解析】 （1） ，因为 ，所以 ，即函数 为减函数， 因为 ，所以值域为 . （2）因为 x∈ ， x∈[2，3]，使得f(x)≥g(x)， 1 2 1 2 ∀ ∃ 所以 ， 因为 ，所以 ， 所以 ，即 . 19.（2020·甘肃省岷县第一中学高二开学考试（理））已知函数 ． （1）求函数 的单调区间． （2）若 对 恒成立，求实数 的取值范围. 【答案】（1）单调增区间 单调减区间 （2） 【解析】 （1）令 ，解得 或 ， 令 ，解得： . 故函数 的单调增区间为 ，单调减区间为 . （2）由（1）知 在 上单调递增，在 上单调递减，在 上单调递增， 又 ， ， ， ∴ ， ∵ 对 恒成立，∴ ，即 ，∴ 20．（2020·南昌县莲塘第三中学高二期末（理））已知函数 . (Ⅰ)求函数 的单调区间； (Ⅱ)求证：当 时， . 【答案】(1)f(x)的单调增区间为(1，＋∞), 单调减区间为(0，1)；(2)见解析. 【解析】 (1)依题意知函数的定义域为{x|x>0}， ∵f′(x)＝2x-2 = ， 由f′(x)>0， 得x>1; 由f′(x)<0， 得02时，g′(x)>0， ∴g(x)在(2，＋∞)上为增函数， ∴g(x)>g(2)＝4-2ln2-6+4>0， ∴当x>2时， x2-2lnx>3x-4, 即当x>2时 .. f(x)lnx(a2)x2 ax 21.（2020·江西景德镇一中高二期中）已知函数 . f(x) （1）求函数 的单调区间； x0, （2）若对任意 ，函数 f(x) 的图象不在 x 轴上方，求实数a的取值范围. [1,) 【答案】（1）详见解析；（2） . 【解析】f(x)lnx(a2)x2 ax 0, （1）函数 定义域为 ， 1 (a2)x12x1 f(x) 2(a2)xa  则 x x ， a20 f(x)0 f(x) 当 时， ， 递增， 1 1 0 x x 当a20时，令 f(x)0，解得 a2，令 f(x)0，解得 a2 ，  1   1  0, ,     所以 f(x)在 a2递增，在a2 递减； x0, f(x) x （2）若对任意 ，函数 的图象不在 轴上方， f(x)lnx(a2)x2 ax0 x0, 则 ， 恒成立， lnx2x2 a 则 x2 x ，x0, 恒成立， 2x1x1lnx lnx2x2 gx 令gx ，则  x2 x 2 ， x2 x 1 hxx1lnx hx1 0 令 ，则 x ， hx 0, h10 所以 在 递减，而 ， gx0 gx0 0 x1 x1 所以当 时， ，当 时， ， 所以当 x1 时， gx 取得最大值1，所以 a1 ， [1,) 所以实数a的取值范围是 . f xlnxax2 2a1x 22．（2020·四川省阆中东风中学校高三月考（文））已知函数 ，其中a为 a0 常数，且 .f x a2 （1）当 时，求 的单调区间； （2）若 f x 在 x1 处取得极值，且在 0,e 的最大值为1，求a的值.  1 1  1 【答案】（1）在   0, 4  和1,上单调递增，在  4 ,1  上单调递减；（2） a  e2 或a 2. 【解析】 1 4x1x1 1 （1） f xlnx2x2 5x， fx x 4x5 x ，令 fx0，得 x 4 或1，则列 表如下：  1 1 1  x  0,   ,1  1 1,  4 4 4  f x + 0 _ 0 + f x 增 极大值 减 极小值 增  1 1  0, ,1 所以 f x 在   4  和1,上单调递增，在  4  上单调递减. 2ax1x1 fx （2）∵ x ， 1 x  令 fx0 ， x 1 ， 2 2a ， 1 f x x1 因为 在 处取得极值， 1 x   x 1 所以 2 2a 1 ， 1 0 f x 0,1 1,e ①2a 时， 在 上单调递增，在 上单调递减， f x 1,e f 1 f 11 a 2 所以 在区间 上的最大值为 ，令 ，解得 ；1 x  0 ②当a0， 2 2a ； 1  1   1  (i)当2a 1 时， f x 在   0, 2a  上单调递增，  2a ,1  上单调递减， 1,e 上单调递增， 1 x 所以最大值1可能在 2a或xe处取得，而 2  1  1  1  1 1 1 f ln a 2a1 ln  10     ， 2a 2a 2a 2a 2a 4a f elneae2 2a1e1 ∴ ， 1 a  ∴ e2 ， 1  1   1  (ii)当 1 2a e 时， f x 在区间 0,1 上单调递增；   1, 2a  上单调递减，  2a ,e  上单调递增， x1 xe f 1ln1a2a10 所以最大值1可能在 或 处取得而 ， 1 1 所以 f elneae2 2a1e1 ，解得 a  e2 ，与 1 x 2  2a e 矛盾； 1 (iii)当 x 2  2a e 时， f x 在区间 0,1 上单调递增，在 1,e 单调递减， x1 f 1ln1a2a10 所以最大值1可能在 处取得，而 ，矛盾， 1 a  综上所述， e2 或a 2.