文档内容
专题 5.4 三角函数图像与性质
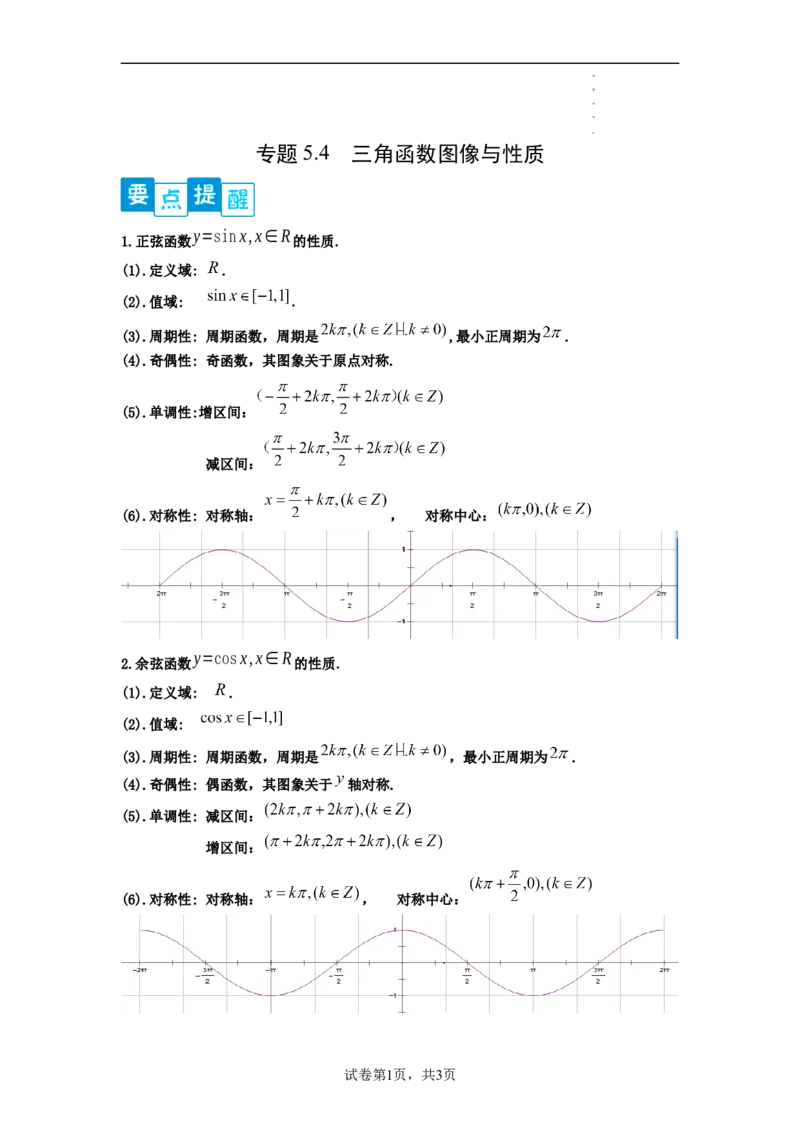
y=sinx,x∈R
1.正弦函数 的性质.
(1).定义域: .
(2).值域: .
(3).周期性: 周期函数,周期是 ,最小正周期为 .
(4).奇偶性: 奇函数,其图象关于原点对称.
(5).单调性:增区间:
减区间:
(6).对称性: 对称轴: , 对称中心:
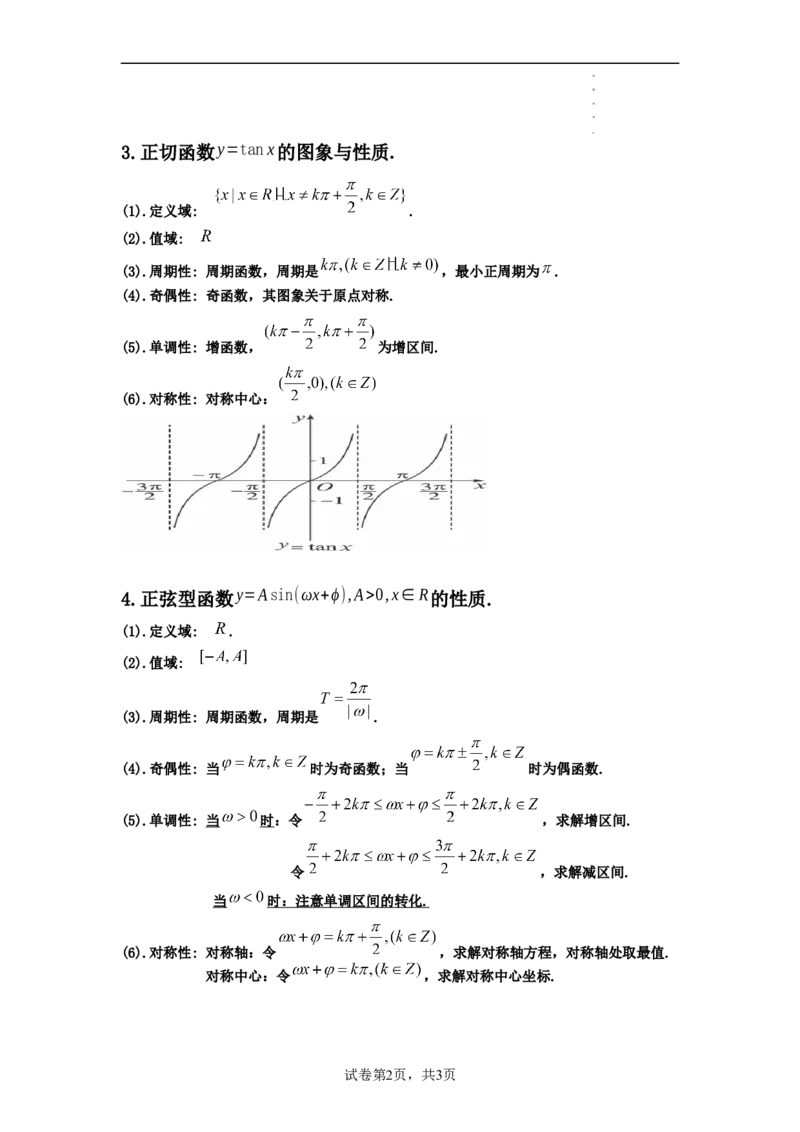
y=cosx,x∈R
2.余弦函数 的性质.
(1).定义域: .
(2).值域:
(3).周期性: 周期函数,周期是 ,最小正周期为 .
(4).奇偶性: 偶函数,其图象关于 轴对称.
(5).单调性: 减区间:
增区间:
(6).对称性: 对称轴: , 对称中心:
试卷第1页,共3页
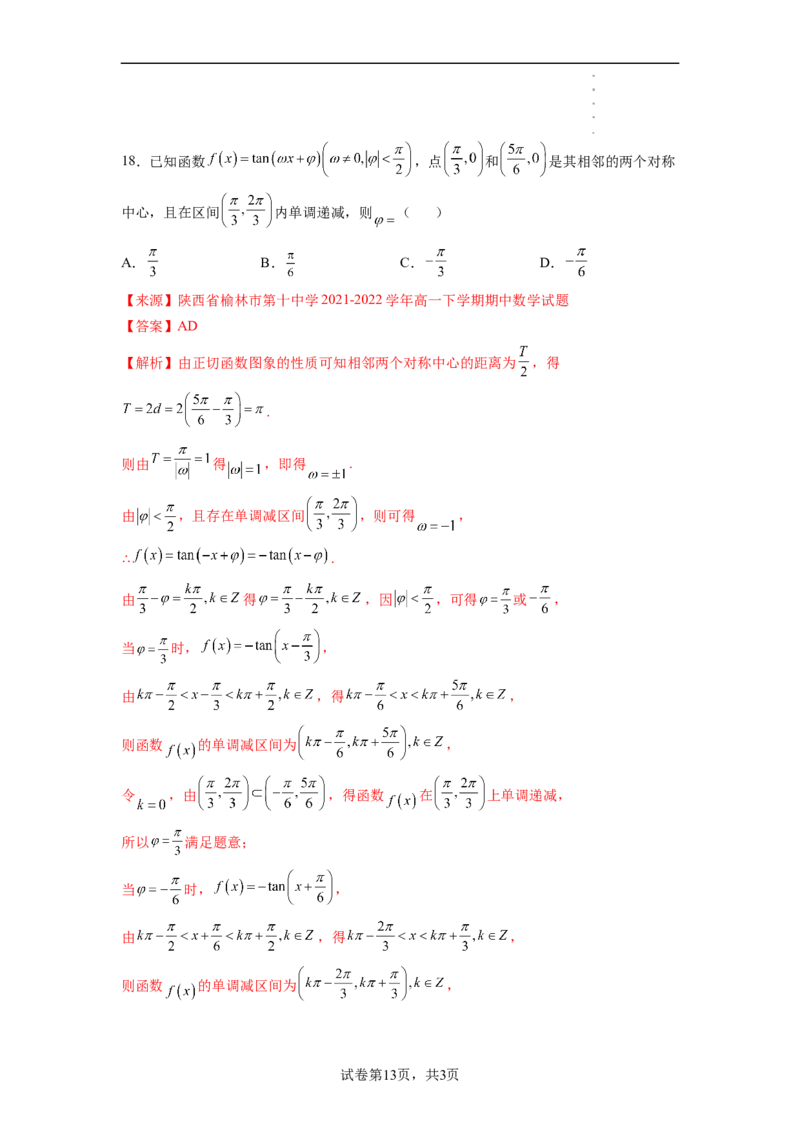
学科网(北京)股份有限公司3.正切函数y=tanx的图象与性质.
(1).定义域: .
(2).值域:
(3).周期性: 周期函数,周期是 ,最小正周期为 .
(4).奇偶性: 奇函数,其图象关于原点对称.
(5).单调性: 增函数, 为增区间.
(6).对称性: 对称中心:
4.正弦型函数y=Asin(ωx+ϕ),A>0,x∈R的性质.
(1).定义域: .
(2).值域:
(3).周期性: 周期函数,周期是 .
(4).奇偶性: 当 时为奇函数;当 时为偶函数.
(5).单调性: 当 时:令 ,求解增区间.
令 ,求解减区间.
当 时:注意单调区间的转化 .
(6).对称性: 对称轴:令 ,求解对称轴方程,对称轴处取最值.
对称中心:令 ,求解对称中心坐标.
试卷第2页,共3页
学科网(北京)股份有限公司5.余弦型函数y=Acos(ωx+ϕ),A>0,x∈R的性质.
(1).定义域: .
(2).值域:
(3).周期性: 周期函数,周期是 .
(4).奇偶性: 当 时为偶函数;当 时为奇函数.
(5).单调性: 当 时:令 ,求解减区间.
令 ,求解增区间.
当 时:注意单调区间的转化 .
(6).对称性: 对称轴:令 ,求解对称轴方程,对称轴处取最值.
对称中心:令 ,求解对称中心坐标.
一、单选题
1.已知函数 ,则( )
A. 的最小正周期为 ,对称中心为
B. 的最小正周期为 ,对称中心为
C. 的最小正周期为 ,对称中心为
D. 的最小正周期为 ,对称中心为
【来源】陕西省榆林市第十中学2021-2022学年高一下学期第一次月考数学试题
【答案】D
【解析】因为函数 ,
所以 的最小正周期为 ,对称中心为 ,故选:D
试卷第3页,共3页
学科网(北京)股份有限公司2.用“五点法”作函数 在一个周期内的图像时,第四个关键点的坐标是
A. B.
C. D.
【答案】A
【解析】
令 ,得 .∴该点坐标为 .故选A
3.若函数 在区间 内没有最值,则 的取值范围是
( )
A. B.
C. D.
【来源】江西省新余市2021-2022学年高一下学期期末考试数学试题
【答案】A
【解析】:函数 的单调区间为 ,
由 ,
得 .
函数 在区间 内没有最值,
函数 在区间 内单调, ,
试卷第4页,共3页
学科网(北京)股份有限公司解得 由 ,得 .
当 时,得 ,
当 时,得 ,又 ,故 ,
综上得 的取值范围是 故选A
4.已知函数 在区间 内单调递减,则实数ω的取值范围是
( )
A. B. C. D.
【来源】山东省济宁市2021-2022学年高一下学期期末数学试题
【答案】B
【解析】:依题意 ,即 ,又 ,所以 ,解得 ,
又 ,所以 ,所以 ,
要使函数在 内单调递减,所以 ,解得 ,
即 ;故选:B
5.已知 是 上的奇函数,若 的图象关于直线
对称,且 在区间 内是单调函数,则 ( )
试卷第5页,共3页
学科网(北京)股份有限公司A. B. C. D.
【来源】5.4 三角函数的图像与性质
【答案】A
【解析】因为 是 上的奇函数,则 ,
所以, ,
因为 的图象关于直线 对称,则 ,可得 ,
当 时, ,
因为函数 在区间 内是单调函数,则 ,解得 ,
所以, , ,故 ,因此, .故选:A.
6.函数 的值域为( )
A. B.
C. D.
【来源】安徽省合肥市第六中学、第八中学、168中学等校2021-2022学年高一上学期期末
联考数学试题
【答案】A
【解析】设 ,因为 ,所以 ,
因为正切函数 在 上为单调递增函数,且 ,
所以 .
∴函数 的值域为 ,
故选:A.
试卷第6页,共3页
学科网(北京)股份有限公司7.已知 且 ,则 的取值范围为( )
A. B.
C. D.
【来源】陕西省渭南市韩城市2021-2022学年高一下学期期末数学试题
【答案】B
【解析】:因为 在 上单调递增,
当 时 ,则 即 ,解得 ,所以
,
当 时 ,则 即 ,解得 ,所以
,当 时 ,此时 无意义,故舍去,
综上可得 .故选:B
8.已知函数 在 上单调递增,则 的值可以是( )
A. B. C. D.
【答案】B
【解析】当 时, ,则 ,解得
,
当 时, ,结合选项可知,只有B选项符合.故选:B.
试卷第7页,共3页
学科网(北京)股份有限公司9.函数 的一个单调递减区间是( )
A. B. C. D.
【答案】B
【解析】解 得, ,
时, ; 时, ; 时, ,
是 的一个单调递减区间.
故选:B.
10.已知函数 在 上有且只有4个零点,则 取值范围是
( )
A. B. C. D.
【来源】辽宁省沈阳市第三十一中学、丹东二中2021-2022学年高一下学期期中考试数学
试题
【答案】B
【解析】由题意, , ,∴ ,解得
.故选:B.
11.函数 的定义域是( )
A. B.
C. D.
【来源】河南省濮阳市2021-2022学年高一上学期期末数学试题
【答案】B
【解析】令 ,则 ,故选:B.
试卷第8页,共3页
学科网(北京)股份有限公司12.函数 的单调减区间是( )
A. B.
C. D.
【来源】陕西省宝鸡市渭滨区2021-2022学年高一下学期期末数学试题
【答案】A
【解析】 ,要求函数 的单调减区间,即求函
数 的单调增区间.
令 ,
所以 .故选:A.
13.已知函数 为偶函数,则 的取值可以为( )
A. B. C. D.0
【来源】浙江省金华第一中学2021-2022学年高一(2-4班)下学期开学检测数学试题
【答案】A
【解析】因函数 为偶函数,则 ,显然 时, ,
即A满足,B,C,D都不满足.故选:A
14.记函数 ( )的最小正周期为 .若 ,且
的图象关于点 中心对称,则 ( )
A.1 B. C. D.3
【来源】辽宁省铁岭市昌图县第一高级中学2021-2022学年高一下学期期末数学试题
【答案】D
试卷第9页,共3页
学科网(北京)股份有限公司【解析】:函数 的最小正周期为 ,
则 ,由 ,得 , ,
的图像关于点 中心对称, ,
且 ,则 , .
, ,取 ,可得 .
,则 .故选:D.
15.已知函数 的最大值为4,最小值为0,且该函
数图象的相邻两个对称轴之间的最短距离为 ,直线 是该函数图象的一条对称轴,
则该函数的解析式是( )
A. B.
C. D.
【来源】北京市中国人民大学附属中学 2021-2022学年高一下学期期末数学模拟练习试题
【答案】B
【解析】因为函数 的最大值为4,最小值为0,
所以 ,解得 ,
因为该函数图象的相邻两个对称轴之间的最短距离为 ,
所以 ,所以 ,
所以 ,得 ,所以 ,
因为直线 是该函数图象的一条对称轴,
试卷第10页,共3页
学科网(北京)股份有限公司所以 ,得 ,因为 ,所以 ,
所以 ,故选:B
二、多选题
16.已知函数 ,则下列说法正确的是( )
A. 在定义域内是增函数 B. 是奇函数
C. 的最小正周期是 D. 图像的对称中心是
【来源】辽宁省大连市第八中学2021-2022学年高一下学期4月阶段性测试数学试题
【答案】BD
【解析】A错误,∵ 的定义域是 ,其在定
义域内的每一个区间上都是单调递增函数,但在整个定义域上没有单调性;
B正确, ,易知其是奇函数;
C错误,函数 的最小正周期为 ;
D正确,令 ,解得 ,所以 图像的对称中心是
.
故选:BD.
17.已知 为 上的奇函数,且当 时, ,记 ,
下列结论正确的是( )
A. 为奇函数
B.若 的一个零点为 ,且 ,则
C. 在区间 的零点个数为3个
试卷第11页,共3页
学科网(北京)股份有限公司D.若 大于1的零点从小到大依次为 ,则
【来源】江西省上饶中学2021-2022学年高一下学期第一次月考数学试题
【答案】ABD
【解析】因为 ,
所以函数 为奇函数,故A正确;假设 ,即 , 时,
,
所以当 , 时, ,
当 , 时, ,
当 , ,则 ,由于 的一个零点为 ,则
,故B正确;
如图:
当 时,令 , ,则 大于0的零点为 , ,的交点,
由图可知,函数 在区间 的零点有2个,由于函数 为奇函数,则函数 在
区间 的零点有1个,并且 ,所以函数在区间 的
零点个数为4个,故C错误;
由图可知, 大于1的零点, , ,所以 ,
而 ,故推出 ,故D正确.
故选:ABD.
试卷第12页,共3页
学科网(北京)股份有限公司18.已知函数 ,点 和 是其相邻的两个对称
中心,且在区间 内单调递减,则 ( )
A. B. C. D.
【来源】陕西省榆林市第十中学2021-2022学年高一下学期期中数学试题
【答案】AD
【解析】由正切函数图象的性质可知相邻两个对称中心的距离为 ,得
.
则由 得 ,即得 .
由 ,且存在单调减区间 ,则可得 ,
∴ .
由 得 ,因 ,可得 或 ,
当 时, ,
由 ,得 ,
则函数 的单调减区间为 ,
令 ,由 ,得函数 在 上单调递减,
所以 满足题意;
当 时, ,
由 ,得 ,
则函数 的单调减区间为 ,
试卷第13页,共3页
学科网(北京)股份有限公司令 ,由 ,得函数 在 上单调递减,
所以 满足题意;
综上可得: 或 满足题意.故选:AD.
19.设函数 ,若 在 上有且仅有3条对称轴,则
( )
A. 在 上有且仅有2个最大值点
B. 在 上有且仅有2个零点
C. 的取值范围是
D. 在 上单调递增
【来源】江西省上饶市六校2021-2022学年高一下学期期末联考数学试题
【答案】ACD
【解析】∵ , ,
∴ ,∴ ,
令 ,∴ ,
画出 图象进行分析:
对于A选项:由图象可知: 在 上有且仅有 , 对应的这2个最大值点,故A
选项正确;
对于B选项:当 ,即 时, 在 有且仅有2个零点;
当 ,即 时, 在 有且仅有3个零点,故B选项不正
试卷第14页,共3页
学科网(北京)股份有限公司确;
对于C选项:∵ 在 有且仅有3条对称轴,
∴ ,∴ ,
∴ 的取值范围是 ,故C选项正确;
对于D选项:∵ , ,∴ ,∴ ,
由C选项可知, ,∴ ,
即 在 上单调递增,故D选项正确.
故选:ACD.
20.已知函数 ,则下列命题正确的是( )
A.若 在 上有10个零点,则
B.若 在 上有11条对称轴,则
C.若 = 在 上有12个解,则
D.若 在 上单调递减,则
【来源】云南省保山市2021-2022学年高一下学期期末质量监测数学试题
【答案】ACD
【解析】
【分析】:因为 ,所以 ,
对于A,因为 在 上有10个零点,
所以 ,解得 ,故A正确;
对于B,若 在 上有11条对称轴,
所以 ,解得 ,故B错误;
试卷第15页,共3页
学科网(北京)股份有限公司对于C,若 = 在 上有12个解,又 ,
所以 ,解得 ,故C正确;
对于D,因为 ,所以 ,
若 在 上单调递减,
则 ,解得 ,
又因 ,所以 ,故D正确.
故选:ACD.
21.函数 ,对于任意的 ,方程 仅
有一个实数根,则m的取值可以为( )
A. B. C. D.
【来源】辽宁省沈阳市第一中学2021-2022学年高一下学期第三次阶段数学试题
【答案】AC
【解析】由 可得: .
因为 ,所以 .
因为 ,所以 .
因为对于任意的 ,方程 仅有一个实数根,
所以 ,解得: .
对照四个选项,只有A、C在 .故选:AC
试卷第16页,共3页
学科网(北京)股份有限公司22.已知函数 ,则下列关于 的判断正确的是( )
A.在区间 上单调递增 B.最小正周期是
C.图象关于直线 成轴对称 D.图象关于点 成中心对称
【来源】黑龙江省哈尔滨市第一六二中学校2021-2022学年高一上学期期末数学试题
【答案】ABD
【解析】对于选项A, 时, ,此时 为增函数;
对于选项B, 的最小正周期为 ;
对于选项C,因为 , ,所以图象不是关于直线 成轴
对称;对于选项D,令 , ,得 ,令 得 ,所以图象关于
点 成中心对称.故选:ABD.
三、解答题
23.已知
(1)函数 ( )在区间 上恰有三条对称轴,求 的取值范围.
(2)函数 ,
①当 时,求函数 (x)的零点;
②当 ,恒有 ,求实数 的取值范围.
【来源】宁夏银川唐徕回民中学2021-2022学年高一下学期期中考试数学试题
【答案】(1)
(2)① 或 ;②
【解析】(1)解:当 时, ,
由函数 ( )在区间 上恰有三条对称轴,
所以 ,
试卷第17页,共3页
学科网(北京)股份有限公司解得 ;
(2)解:①当 时,令 得 ,
因为 ,所以 ,
即 ,
因为 ,所以 ,
因为 ,所以 或 ;
②令 ,则 ,
函数 ,对称轴 ,
当 即 , ,得 ,
所以 ,
当 即 ,令 ,得 ,
所以 ,
当 即 ,令 ,得 ,
所以 ,
综上:为实数 的取值范围为 .
24.已知函数 ,图象上任意两条相邻对称轴间的距离为 .
(1)求函数的单调区间和对称中心.
(2)若关于 的方程 在 上有实数解,求实数 的取值范围.
【答案】(1)答案见解析(2)
【解析】(1)函数 ,图象上任意两条相邻对称轴间的距离为 .
周期 ,即 ,那么 ,可得 .
试卷第18页,共3页
学科网(北京)股份有限公司,
令 , ,解得 , ,
可得函数的单调递增区间 , ,
令 , ,解得 , ,
∴可得函数的单调递减区间 ,
令 ,解得 ,可得对称中心为 ;
(2)
方程 在 上有实数解,即 在
上有实数解,
令 , 上, ,
则 在 上有解, ,
易得 在 上单调递增,且 时, ,所以 ,
所以 范围为 .
25.已知函数 .
(1)请用五点法做出 一个周期内的图像;
(2)若函数 在区间 上有两个零点,请写出 的取值范围,无需说明理由.
【来源】北京市石景山区2021-2022学年高一下学期期末数学试题
【答案】(1)答案见解析
(2)
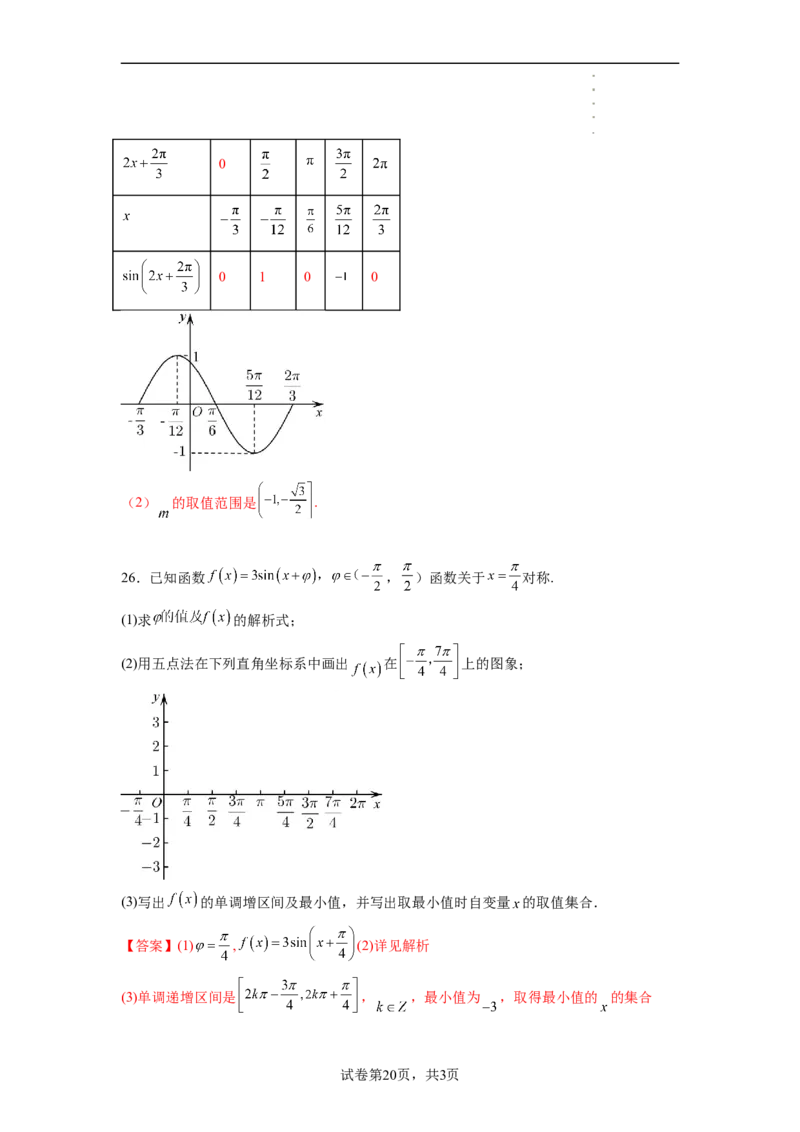
【解析】(1)列表
试卷第19页,共3页
学科网(北京)股份有限公司0
0 1 0 0
(2) 的取值范围是 .
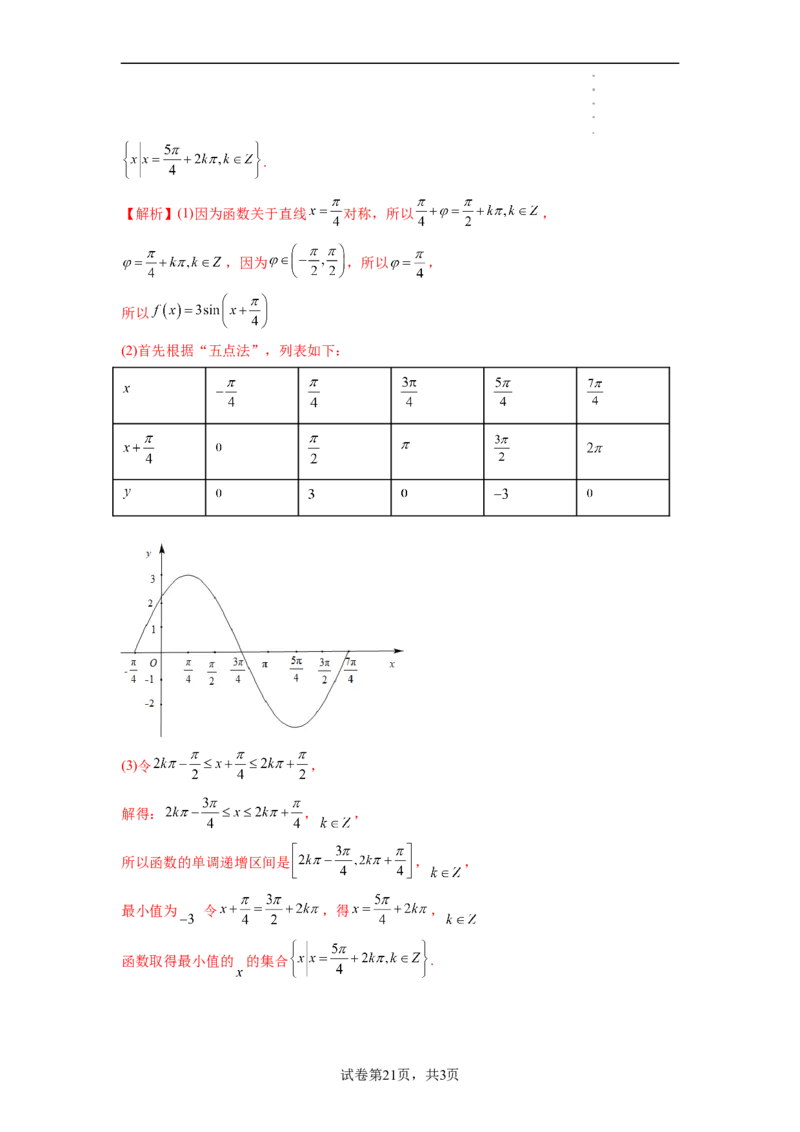
26.已知函数 , )函数关于 对称.
(1)求 的解析式;
(2)用五点法在下列直角坐标系中画出 在 上的图象;
(3)写出 的单调增区间及最小值,并写出取最小值时自变量 的取值集合.
【答案】(1) , (2)详见解析
(3)单调递增区间是 , ,最小值为 ,取得最小值的 的集合
试卷第20页,共3页
学科网(北京)股份有限公司.
【解析】(1)因为函数关于直线 对称,所以 ,
,因为 ,所以 ,
所以
(2)首先根据“五点法”,列表如下:
(3)令 ,
解得: , ,
所以函数的单调递增区间是 , ,
最小值为 令 ,得 ,
函数取得最小值的 的集合 .
试卷第21页,共3页
学科网(北京)股份有限公司27.已知函数 .
(1)求函数 的单调递增区间;
(2)求函数 在区间 上的所有零点之和.
【来源】陕西省西安市蓝田县2021-2022学年高一下学期期末数学试题
【答案】(1) (2)
【解析】(1)解:由 ,解得 .
函数 的单调递增区间为 .
(2)解:由 ,得 ,则 或
. 或 又 , 或
或 .即函数 在区间 上的所有零点为 , , ,故零点之和为
.
试卷第22页,共3页
学科网(北京)股份有限公司