文档内容
2023-2024学年上海师大附中闵行分校高一(下)期末数学试卷
一、填空题(本大题共有12小题,满分54分)考生应在答题纸相应编号的空格内直接填写结果,1-6题
每个空格填对得4分,7-12题每个空格填对得5分,否则一律得0分。
1.(4分)若复数z=(m2﹣m﹣2)+i(m2﹣4)是纯虚数,则实数m= .
2.(4分)已知向量 =(x,1), =(﹣2,2),若 ,则实数x= .
3.(4分)函数f(x)=sin2x的最小正周期为 .
4.(4分)若角 的终边过点P(4,﹣3),则 = .
5.(4分)在等差α数列{a }中,a =1940,a +a =2024,则a = .
n 1940 102 1922 84
6.(4分)设k R,向量 =(3,4), =(k,﹣1).若 在 方向上的数量投影为 1,则k=
∈
.
7.(5分)方程cos2x﹣sinx=0在区间[0,2 ]上的所有解的和为 .
8.(5分)关于x的实系数一元二次方程x2+ π kx+3=0有两个虚根x 和x ,若 ,则实数k
1 2
= .
9.(5分)已知函数f(x)=sin( x)( >0)在[0,3 ]有且仅有5个零点,则实数 的取值范围是
. ω ω π ω
10.(5分)设无穷数列{a }的前n项和为S .若S =2n+1+n﹣2,则 = .
n n n
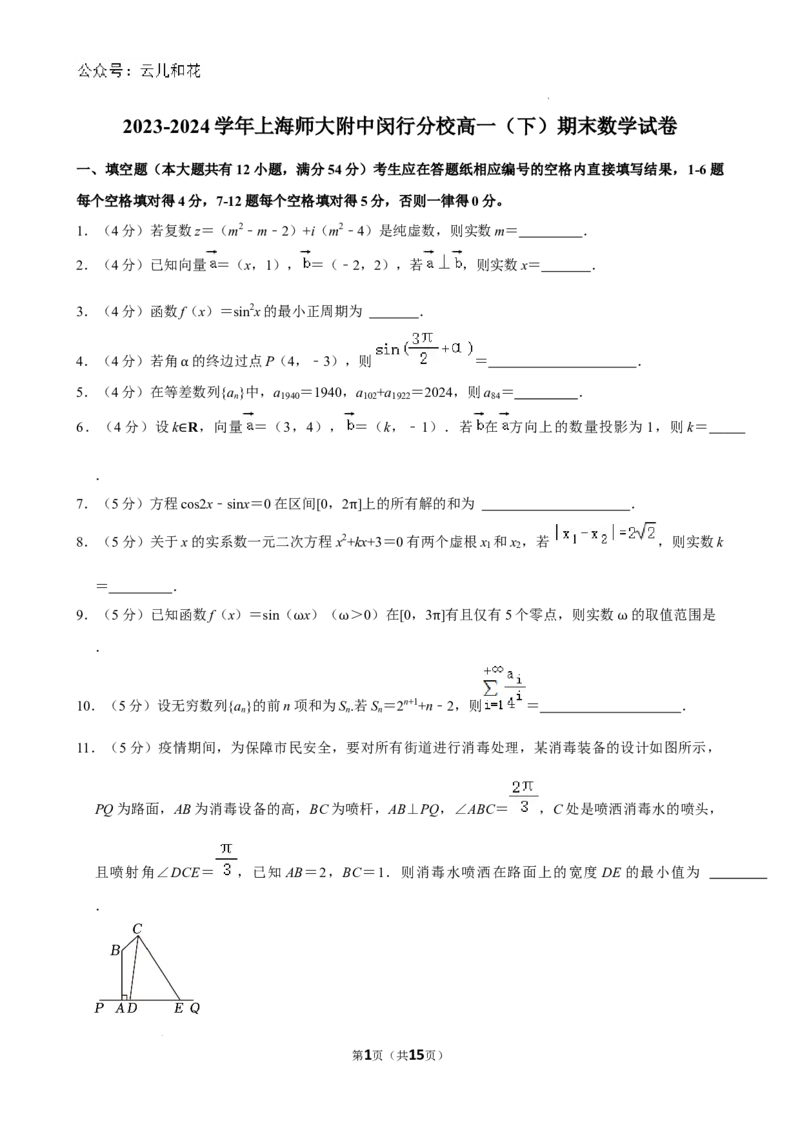
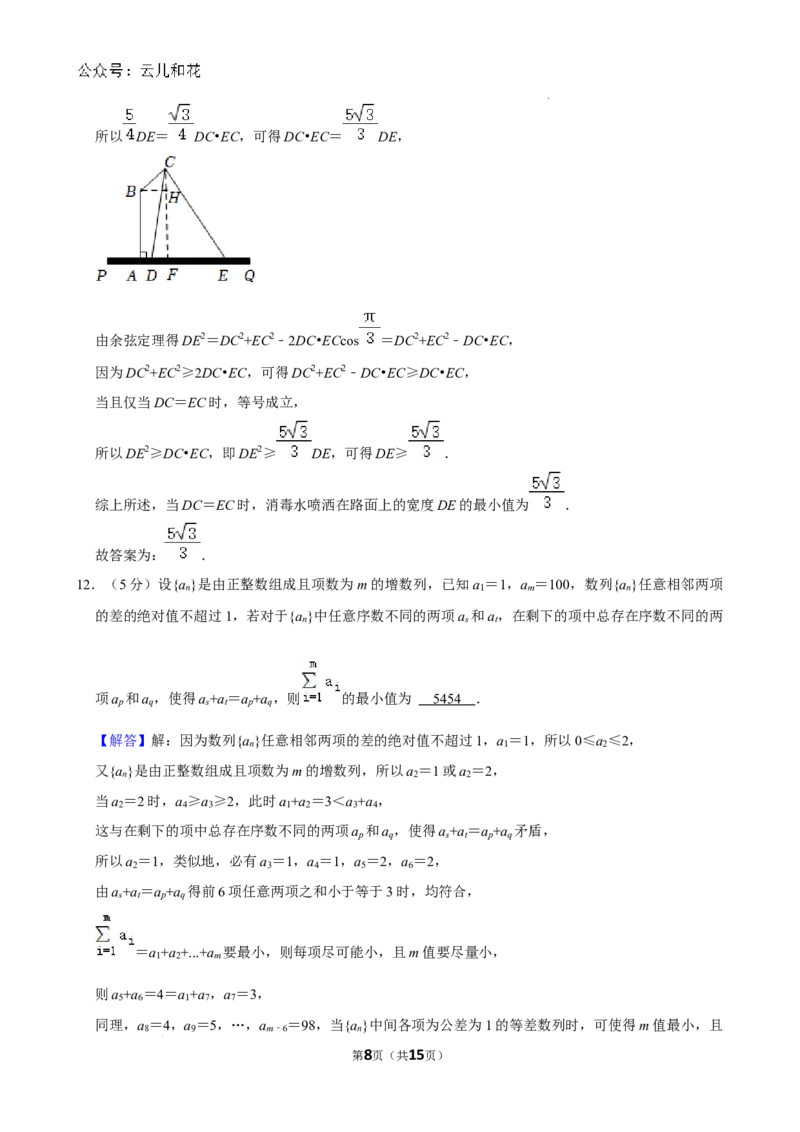
11.(5分)疫情期间,为保障市民安全,要对所有街道进行消毒处理,某消毒装备的设计如图所示,
PQ为路面,AB为消毒设备的高,BC为喷杆,AB⊥PQ,∠ABC= ,C处是喷洒消毒水的喷头,
且喷射角∠DCE= ,已知 AB=2,BC=1.则消毒水喷洒在路面上的宽度 DE的最小值为
.
第1页(共15页)
学科网(北京)股份有限公司12.(5分)设{a }是由正整数组成且项数为m的增数列,已知a =1,a =100,数列{a }任意相邻两项
n 1 m n
的差的绝对值不超过1,若对于{a }中任意序数不同的两项a 和a,在剩下的项中总存在序数不同的两
n s t
项a 和a ,使得a+a=a +a ,则 的最小值为 .
p q s t p q
二、选择题(本大题共有4题,满分18分,第13、14题每题4分,第15、16题每题5分)每题有且只
有一个正确选项。考生应在答题纸的相应位置,将代表正确选项的小方格涂黑。
13.(4分)已知等差数列{a }中,a +a +a = ,那么cos(a +a )=( )
n 1 4 7 3 5
A. B.﹣ C. D.﹣
14.(4分)已知函数 ,x R,则下列判断不正确的是( )
∈
A.﹣2≤f(x)≤2
B.f(x)在区间(0, )上只有1个零点
C.f(x)的最小正周期π为
π
D.直线 为函数f(x)图象的一条对称轴
15.(5分)设O是△ABC的外心,若 ,则 =( )
A.2 B. C. D.
16.(5分)已知复数z ,z 和z满足|z |=|z |=1,若|z ﹣z |=|z ﹣1|=|z ﹣z|,则|z|的最大值为( )
1 2 1 2 1 2 1 2
A. B.3 C. D.1
三、解答题(本大题满分78分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写
出必要的步骤。
17.(14分)已知复数z是纯虚数,(z+2)2﹣8i是实数.
(1)求z;
(2)若 ,求|z |.
1
第2页(共15页)
学科网(北京)股份有限公司18.(14分)已知函数 的图象与x轴的交
点中,相邻两个交点之间的距离为 ,且图象上一个最低点为 .
(1)求f(x)的解析式和周期.
(2)当 时,求f(x)的值域.
19.(14分)某工厂为扩大生产规模,今年年初新购置了一条高性能的生产线,该生产线在使用过程中
的维护费用会逐年增加,第一年的维护费用是4万元,从第二年到第七年,每年的维护费用均比上年
增加2万元,从第八年开始,每年的维护费用比上年增加25%.
(I)设第n年该生产线的维护费用为a ,求a 的表达式;
n n
(Ⅱ)若该生产线前n年每年的平均维护费用大于12万元时,需要更新生产线,求该生产线前 n年每
年的平均维护费用,并判断第几年年初需要更新该生产线?
20.(18分)在直角坐标平面xOy上的一列点A (1,a ),A (2,a )…A (n,a ),…,简记为
1 1 2 2 n n
{A }.若由b = 构成的数列{b }满足b >b ,n=1,2,…,其中 =(0,1),则称{A }
n n n n+1 n n
为“M点列”.
(1)判断A (1,1),A (2,1),A (3,1),…,A (n,1),是否为“M点列”,并说明理
1 2 3 n
由;
(2)判断A (1,1),A (2, ),A (3, ),…,A (n, ).是否为“M点列”,请说明
1 2 3 n
理由,并求出此时数列{b }的前n项和T ;
n n
(3)若 A 为“M 点列”,且点 A 在 A 的右上方,任取其中连续三点 A ,A ,A ,判断
n 2 1 k k+1 2+2
△A A A 的形状(锐角三角形、直角三角形、钝角三角形),并予以证明.
1 k+1 k+2
21.(18分)定义向量 的“对应函数”为y=asinx+bcosx;函数y=asinx+bcosx的“对应向
量”为 (其中O为坐标原点).记平面内所有向量的“对应函数”构成的集合为S.
(1)设 ,求证:y=g(x) S;
∈
(2)已知 且y=h(x) S, 是函数y=
∈
第3页(共15页)
学科网(北京)股份有限公司h(x)的“对应向量”, ,求 ;
(3)已知 ,向量 的“对应函数”y=f(x)在x=x 处
0
取得最大值,当 变化时,求tan2x 的取值范围.
0
θ
参考答案与试题解析
一、填空题(本大题共有12小题,满分54分)考生应在答题纸相应编号的空格内直接填写结果,1-6题
每个空格填对得4分,7-12题每个空格填对得5分,否则一律得0分。
1.(4分)若复数z=(m2﹣m﹣2)+i(m2﹣4)是纯虚数,则实数m= ﹣ 1 .
【解答】解:z=(m2﹣m﹣2)+i(m2﹣4)是纯虚数,
则 ,解得m=﹣1.
故答案为:﹣1.
2.(4分)已知向量 =(x,1), =(﹣2,2),若 ,则实数x= 1 .
【解答】解:向量 =(x,1), =(﹣2,2), ,
则﹣2x+2=0,解得x=1.
故答案为:1.
3.(4分)函数f(x)=sin2x的最小正周期为 .
π
【解答】解:∵f(x)=sin2x= ﹣ cos2x,
第4页(共15页)
学科网(北京)股份有限公司∴f(x)的最小正周期T= = .
故答案为: . π
π
4.(4分)若角 的终边过点P(4,﹣3),则 = ﹣ .
α
【解答】解: =﹣sin( + )=﹣cos ,
∵角 的终边过点P(4,﹣3), α α
α
∴cos = = ,
α
则 =﹣cos =﹣ ,
α
故答案为:﹣
5.(4分)在等差数列{a }中,a =1940,a +a =2024,则a = 8 4 .
n 1940 102 1922 84
【解答】解:等差数列{a }中,a =1940,a +a =2024,
n 1940 102 1922
又a +a =a +a =2024,
1940 84 102 1922
则a =84.
84
6.(4分)设k R,向量 =(3,4), =(k,﹣1).若 在 方向上的数量投影为1,则k= 3 .
∈
【解答】解:由向量 =(3,4), =(k,﹣1),可得 在 方向上的数量投影为:
| |cos< >=| |• = = =1,解得k=3.
故答案为:3.
7.(5分)方程cos2x﹣sinx=0在区间[0,2 ]上的所有解的和为 .
π
【解答】解:由cos2x﹣sinx=0,即1﹣2sin2x﹣sinx=0,解得sinx=﹣1或 ,
在[0,2 ],当sinx=﹣1时 ,当 时 或 ,
π
所以所有解的和为 .
第5页(共15页)
学科网(北京)股份有限公司故答案为: .
8.(5分)关于x的实系数一元二次方程x2+kx+3=0有两个虚根x 和x ,若 ,则实数k
1 2
= ± 2 .
【解答】解:由题意可得, ,
∴k2<12,|x ﹣x |2=| ﹣4x x |=|k2﹣12|=8,
1 2 1 2
∴k2=20或4,
又∵k2<12,
∴k2=4,
∴k=±2.
故答案为:±2.
9.(5分)已知函数f(x)=sin( x)( >0)在[0,3 ]有且仅有5个零点,则实数 的取值范围是
ω ω π ω
[ , ) .
【解答】解:因为x [0,3 ], >0,所以 x [0,3 ],
要使函数有5个零点∈,则3π ω[4 ,5 ),ω ∈ πω
πω∈ π π
解得 的范围为[ , ).
ω
故答案为:[ , ).
10.(5分)设无穷数列{a }的前n项和为S .若S =2n+1+n﹣2,则 = .
n n n
【解答】解:由题意,当n=1时,a =S =22+1﹣2=3,
1 1
当n≥2时,a
n
=S
n
﹣S
n﹣1
=2n+1+n﹣2﹣2n﹣(n﹣1)+2
=2n+1,
∵当n=1时,a =3也满足上式,
1
∴a =2n+1,n N*,
n
∈
第6页(共15页)
学科网(北京)股份有限公司∴ =
= ( + )
= +
= +
=1+
= .
故答案为: .
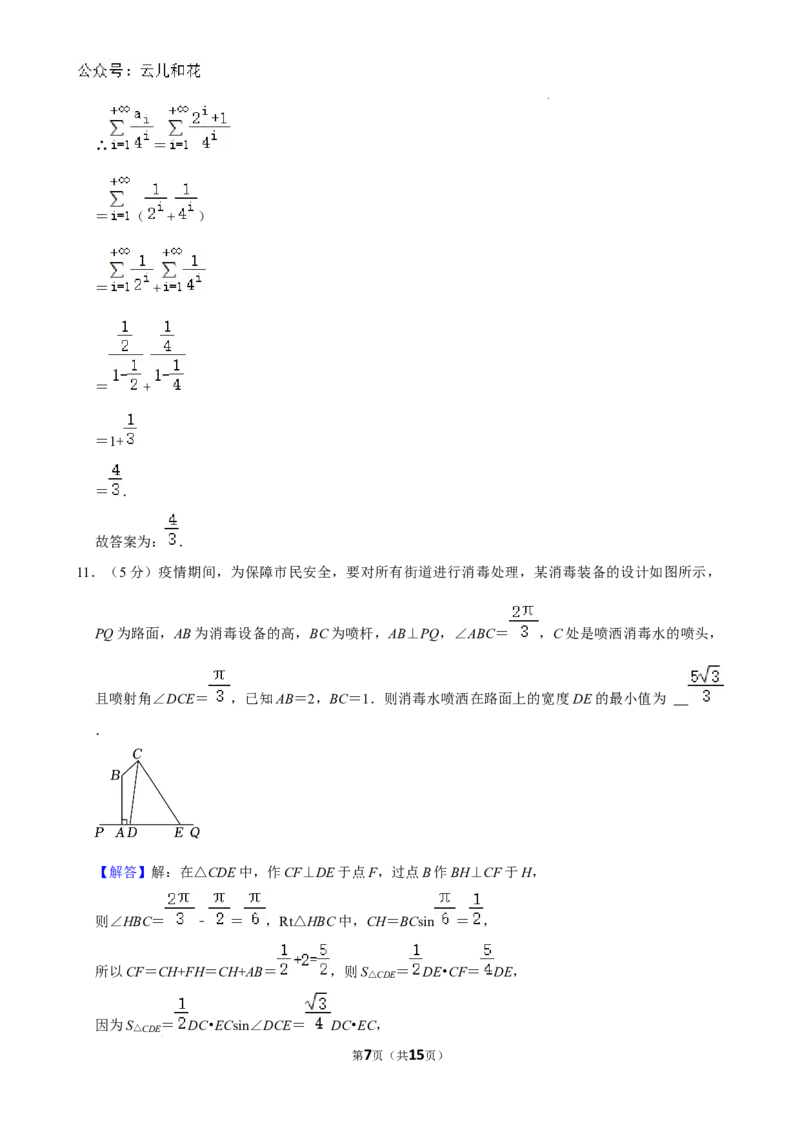
11.(5分)疫情期间,为保障市民安全,要对所有街道进行消毒处理,某消毒装备的设计如图所示,
PQ为路面,AB为消毒设备的高,BC为喷杆,AB⊥PQ,∠ABC= ,C处是喷洒消毒水的喷头,
且喷射角∠DCE= ,已知AB=2,BC=1.则消毒水喷洒在路面上的宽度DE的最小值为
.
【解答】解:在△CDE中,作CF⊥DE于点F,过点B作BH⊥CF于H,
则∠HBC= ﹣ = ,Rt△HBC中,CH=BCsin = ,
所以CF=CH+FH=CH+AB= ,则S△CDE = DE•CF= DE,
因为S△CDE = DC•ECsin∠DCE= DC•EC,
第7页(共15页)
学科网(北京)股份有限公司所以 DE= DC•EC,可得DC•EC= DE,
由余弦定理得DE2=DC2+EC2﹣2DC•ECcos =DC2+EC2﹣DC•EC,
因为DC2+EC2≥2DC•EC,可得DC2+EC2﹣DC•EC≥DC•EC,
当且仅当DC=EC时,等号成立,
所以DE2≥DC•EC,即DE2≥ DE,可得DE≥ .
综上所述,当DC=EC时,消毒水喷洒在路面上的宽度DE的最小值为 .
故答案为: .
12.(5分)设{a }是由正整数组成且项数为m的增数列,已知a =1,a =100,数列{a }任意相邻两项
n 1 m n
的差的绝对值不超过1,若对于{a }中任意序数不同的两项a 和a,在剩下的项中总存在序数不同的两
n s t
项a 和a ,使得a+a=a +a ,则 的最小值为 545 4 .
p q s t p q
【解答】解:因为数列{a }任意相邻两项的差的绝对值不超过1,a =1,所以0≤a ≤2,
n 1 2
又{a }是由正整数组成且项数为m的增数列,所以a =1或a =2,
n 2 2
当a =2时,a ≥a ≥2,此时a +a =3<a +a ,
2 4 3 1 2 3 4
这与在剩下的项中总存在序数不同的两项a 和a ,使得a+a=a +a 矛盾,
p q s t p q
所以a =1,类似地,必有a =1,a =1,a =2,a =2,
2 3 4 5 6
由a+a=a +a 得前6项任意两项之和小于等于3时,均符合,
s t p q
=a +a +...+a 要最小,则每项尽可能小,且m值要尽量小,
1 2 m
则a +a =4=a +a ,a =3,
5 6 1 7 7
同理,a
8
=4,a
9
=5,…,a
m﹣6
=98,当{a
n
}中间各项为公差为1的等差数列时,可使得m值最小,且
第8页(共15页)
学科网(北京)股份有限公司满足已知条件.
由对称性得最后6项为a
m
=a
m﹣1
=a
m﹣2
=a
m﹣3
=100,a
m﹣4
=a
m﹣5
=99,
则 =a +a +...+a 的最小值S= +4×100+3×1+2+99=5454.
1 2 m
故答案为:5454.
二、选择题(本大题共有4题,满分18分,第13、14题每题4分,第15、16题每题5分)每题有且只
有一个正确选项。考生应在答题纸的相应位置,将代表正确选项的小方格涂黑。
13.(4分)已知等差数列{a }中,a +a +a = ,那么cos(a +a )=( )
n 1 4 7 3 5
A. B.﹣ C. D.﹣
【解答】解:∵等差数列{a }中,a +a +a = ,
n 1 4 7
∴a +a +a =3a = ,∴ ,
1 4 7 4
∴a +a =2a = ,
3 5 4
∴cos(a +a )=cos =﹣cos =﹣ .
3 5
故选:B.
14.(4分)已知函数 ,x R,则下列判断不正确的是( )
∈
A.﹣2≤f(x)≤2
B.f(x)在区间(0, )上只有1个零点
C.f(x)的最小正周期π为
π
D.直线 为函数f(x)图象的一条对称轴
【解答】解:由题意, ,
对于A,因为 ,则 ,即﹣2≤f(x)≤2,A正确;
对于 B,由 f(x)=0 得 ,即 ,满足 x (0, )的有
∈ π
第9页(共15页)
学科网(北京)股份有限公司,B错误;
对于C,f(x)的最小正周期为 ,C正确;
对于D,当 时, ,则 ,因此 是f(x)图象的一条对称轴,D正
确.
故选:B.
15.(5分)设O是△ABC的外心,若 ,则 =( )
A.2 B. C. D.
【解答】解:设 ,
则 ,
可得b2=2c2,
故 .
故选:C.
16.(5分)已知复数z ,z 和z满足|z |=|z |=1,若|z ﹣z |=|z ﹣1|=|z ﹣z|,则|z|的最大值为( )
1 2 1 2 1 2 1 2
A. B.3 C. D.1
【解答】解:根据题意,得|z|=|(z ﹣z)﹣z |≤|z ﹣z|+|z |=|z ﹣1|+1≤|z |+1+1=3,
2 2 2 2 1 1
当z =﹣1,z =1,z=3时,|z ﹣z |=|z ﹣1|=|z ﹣z|=2,此时|z|=3,
1 2 1 2 1 2
所以|z| =3.
max
故选:B.
三、解答题(本大题满分78分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写
出必要的步骤。
17.(14分)已知复数z是纯虚数,(z+2)2﹣8i是实数.
(1)求z;
第10页(共15页)
学科网(北京)股份有限公司(2)若 ,求|z |.
1
【解答】解:(1)设z=mi(m R且m≠0).
则(z+2)2﹣8i=4﹣m2+(4m﹣∈8)i为实数,
所以4m﹣8=0,所以m=2,
所以z=2i;
(2)由(1) , ,
所以 .
18.(14分)已知函数 的图象与x轴的交
点中,相邻两个交点之间的距离为 ,且图象上一个最低点为 .
(1)求f(x)的解析式和周期.
(2)当 时,求f(x)的值域.
【解答】解:(1)由题意可得T= =2× ,∴ =2.
ω
根据图象上一个最低点为 ,可得A=2,2sin(2• + )=﹣2,0< < ,
φ φ
可得 = ,∴f(x)=2sin(2x+ ),故它的周期为 = .
φ π
(2)当 时,2x+ [ , ],故当2x+ = 时,函数取得最小值为﹣1;
∈
当2x+ = 时,函数取得最大值为2,故函数的值域为[﹣1,2].
19.(14分)某工厂为扩大生产规模,今年年初新购置了一条高性能的生产线,该生产线在使用过程中
的维护费用会逐年增加,第一年的维护费用是4万元,从第二年到第七年,每年的维护费用均比上年
增加2万元,从第八年开始,每年的维护费用比上年增加25%.
(I)设第n年该生产线的维护费用为a ,求a 的表达式;
n n
(Ⅱ)若该生产线前n年每年的平均维护费用大于12万元时,需要更新生产线,求该生产线前 n年每
第11页(共15页)
学科网(北京)股份有限公司年的平均维护费用,并判断第几年年初需要更新该生产线?
【解答】解:(I)当n≤7时,数列{a }是首项为4,公差为2的等差数列,a =4+2(n﹣1)=2n+2;
n n
当n≥8时,数列{a }是首项为a ,公比为 的等比数列,又a =16,∴a =16×( )n﹣7
n 7 7 n
∴a 的表达式为a = ;
n n
(II)设S 表示数列{a }的前n项和,由等差及等比数列的求和公式得
n n
当1≤n≤7时,Sn=4n+n(n﹣1)=n2+3n…(8分)
当n≥8时,由S =70,S =S +16× × =80• ﹣10.
7 n 7
该生产线前n年每年的平均维护费用 =
当1≤n≤7时,{ }为增数列,
当n≥8时,∵ >0,{ }也为增数列,
又∵ , , ,
则第9年初需要更新该生产线.
20.(18分)在直角坐标平面xOy上的一列点A (1,a ),A (2,a )…A (n,a ),…,简记为
1 1 2 2 n n
{A }.若由b = 构成的数列{b }满足b >b ,n=1,2,…,其中 =(0,1),则称{A }
n n n n+1 n n
为“M点列”.
(1)判断A (1,1),A (2,1),A (3,1),…,A (n,1),是否为“M点列”,并说明理
1 2 3 n
由;
(2)判断A (1,1),A (2, ),A (3, ),…,A (n, ).是否为“M点列”,请说明
1 2 3 n
第12页(共15页)
学科网(北京)股份有限公司理由,并求出此时数列{b }的前n项和T ;
n n
(3)若 A 为“M 点列”,且点 A 在 A 的右上方,任取其中连续三点 A ,A ,A ,判断
n 2 1 k k+1 2+2
△A A A 的形状(锐角三角形、直角三角形、钝角三角形),并予以证明.
1 k+1 k+2
【解答】解:(1)由题意得a =1, =(1,0),
n
所以 ,
不满足b >b ,
n+1 n
故{A }不是”M点列”.
n
(2)由题意得 , ,
所以 ,
显然有b >b ,
n+1 n
所以{A }是M点列,
n
则T
n
=b
1
+b
2
+b
3
+⋯+b
n
= ;
(3)因为{A }为“M点列”,
n
所以A (k,a ),A (k+1,a ),A (k+2,a ),
k k k+1 k+1 k+2 k+2
所以 =(﹣1,a ﹣a ), =(1,a ﹣a ),
k k+1 k+2 k+1
则 ,
因为点A 在点A 的右上方,所以b =a ﹣a >0,
2 1 1 2 1
因为{A }为M点列,所以b ≥b >0,
n n 1
所以(a ﹣a )(a ﹣a )=﹣b b <0,
k+2 k+1 k k+1 k+1 k
则 ,
即 <0,
又∠A A A 为ΔA A A 的内角,
k k+1 k+2 k k+1 k+2
所以∠A A A 为钝角,
k k+1 k+2
所以ΔA A A 为钝角三角形.
k k+1 k+2
第13页(共15页)
学科网(北京)股份有限公司21.(18分)定义向量 的“对应函数”为y=asinx+bcosx;函数y=asinx+bcosx的“对应向
量”为 (其中O为坐标原点).记平面内所有向量的“对应函数”构成的集合为S.
(1)设 ,求证:y=g(x) S;
∈
(2)已知 且y=h(x) S, 是函数y=
∈
h(x)的“对应向量”, ,求 ;
(3)已知 ,向量 的“对应函数”y=f(x)在x=x
0
处取得最大值,当 变化时,求tan2x 的取值范围.
0
θ
【解答】解:(1) =3sinx﹣4cosx,
∴ =(3,﹣4),∴g(x) S;
∈
(2)h(x)=cos(x+ )+2 cos(x﹣ )=cosxcos ﹣sinxsin +2 ( cosx+ sinx)
=(cos +2)cosx+(2α﹣sin )sinx, α α
∵h(x)α S,∴ =(cosα+2,2﹣sin ),
∈ α α
∴ ﹣ =(cos ,﹣sin ),∴( ﹣ )2=cos2 +sin2 =1;
α α α α
(3)y=f(x)=(2+cos )sinx+sin cosx= sin(x+ )(tan =
), θ θ φ φ
∵y=f(x)在x=x 处取得最大值,∴x + = +2k ,∴x = +2k ﹣ ,
0 0 0
φ π π φ
tan2x =tan( +4k ﹣2 )=﹣tan2 =﹣ ,
0
π π φ φ
令t=tan = ,利用函数的有界性得t [﹣ , ],
φ ∈
第14页(共15页)
学科网(北京)股份有限公司tan2x =﹣ =﹣ ,
0
当t=0时,tan2x =0,
0
当t≠0时,tan2x =﹣ 严格递减,得tan2x [﹣ ,0)∪(0, ],
0 0
∈
则tan2x 的取值范围为[﹣ , ].
0
第15页(共15页)
学科网(北京)股份有限公司