吉安市高一下学期期末教学质量检测数学答案_2024-2025高一（7-7月题库）_2025年7月_250704江西省吉安市2024-2025学年高一下学期期末教学质量检测

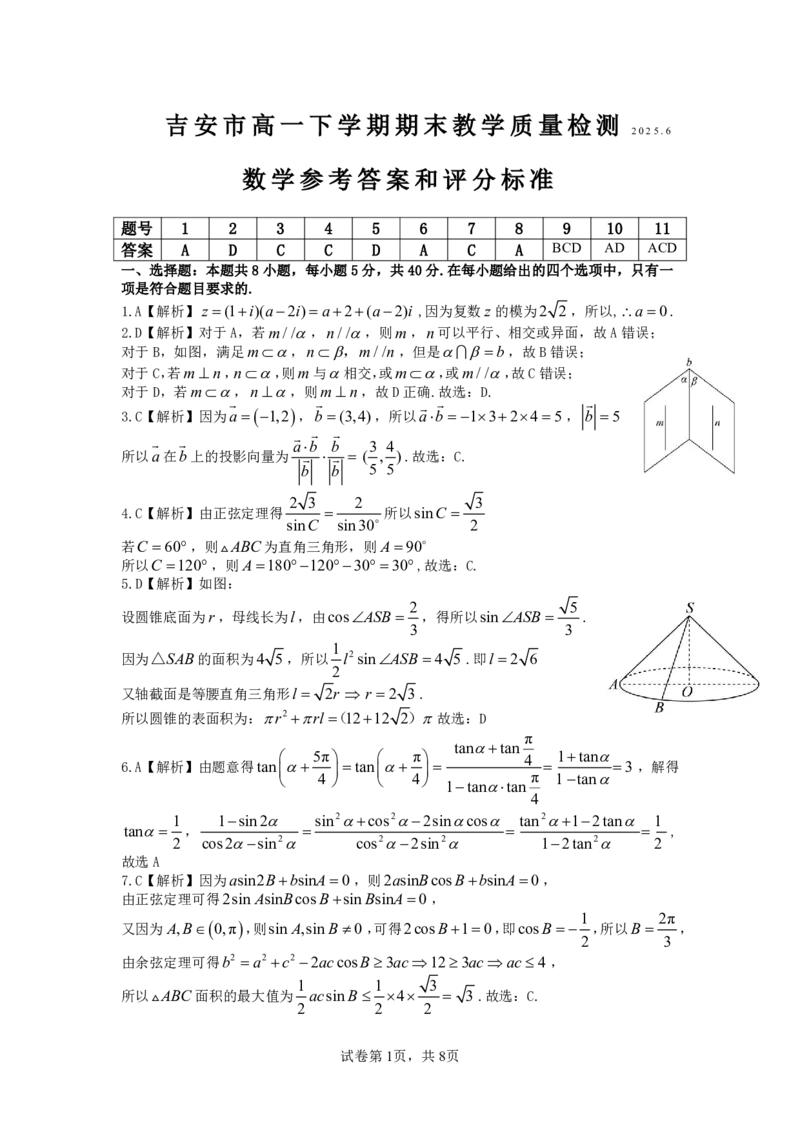
吉 安 市 高 一 下 学 期 期 末 教 学 质 量 检 测 2025.6 数 学 参 考 答 案 和 评 分 标 准 题号 1 2 3 4 5 6 7 8 9 10 11 答案 A D C C D A C A BCD AD ACD 一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一 项是符合题目要求的. 1.A【解析】z (1i)(a2i)a2(a2)i ,因为复数z 的模为2 2，所以,a0. 2.D【解析】对于A，若m//，n//，则m，n可以平行、相交或异面，故A错误； 对于B，如图，满足m，n，m//n，但是b，故B错误； 对于C，若mn，n，则m与相交，或m，或m//，故C错误； 对于D，若m，n，则mn，故D正确.故选：D.      3.C【解析】因为a 1,2 ，b (3,4)，所以ab 13245， b 5      ab b 3 4 所以a在b上的投影向量为     ( , ).故选：C. b b 5 5 2 3 2 3 4.C【解析】由正弦定理得  所以sinC  sinC sin30 2 若C 60，则ABC为直角三角形，则A90 所以C 120，则A1801203030,故选：C. 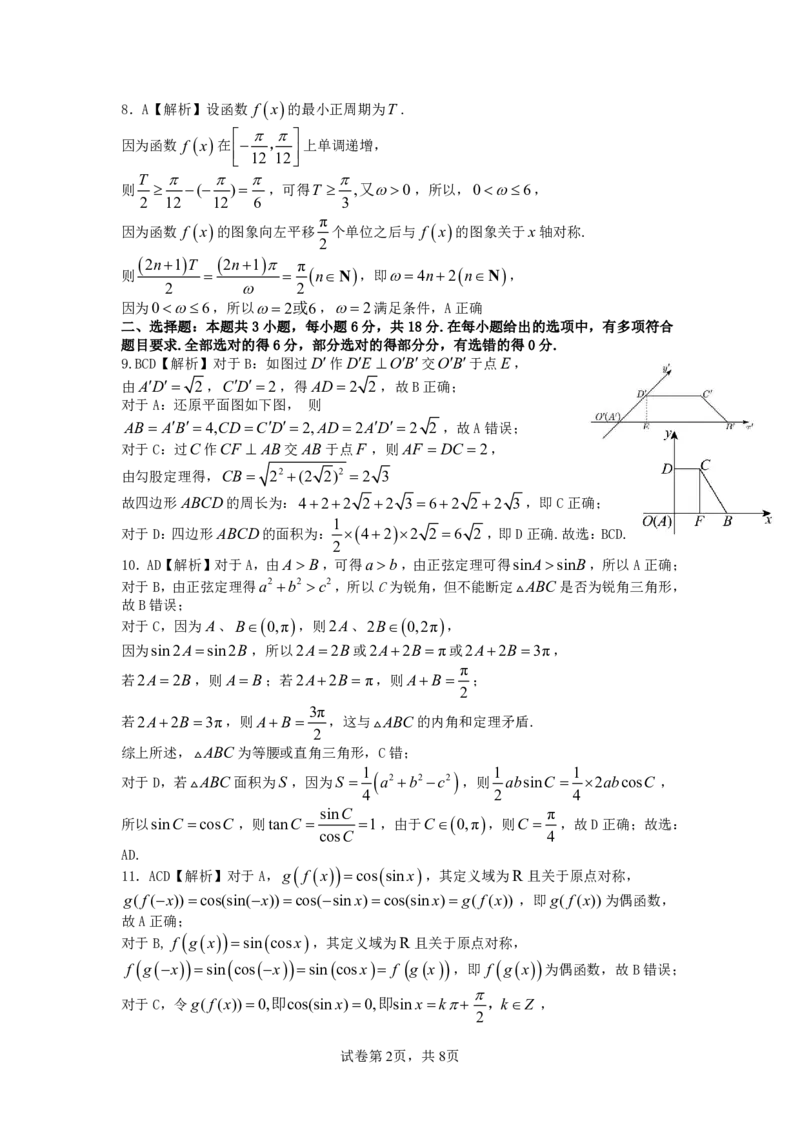5.D【解析】如图： 2 5 设圆锥底面为r，母线长为l，由cosASB ，得所以sinASB . 3 3 1 因为△SAB的面积为4 5，所以 l2sinASB 4 5 .即l 2 6 2 又轴截面是等腰直角三角形l  2r  r 2 3. 所以圆锥的表面积为：r2 rl （1212 2）故选：D π tantan  5π  π 1tan 4 6.A【解析】由题意得tan   tan     3 ，解得  4   4 π 1tan 1tantan 4 1 1sin2 sin2cos22sincos tan212tan 1 tan ，    , 2 cos2sin2 cos22sin2 12tan2 2 故选A 7.C【解析】因为asin2BbsinA0，则2asinBcosBbsinA0， 由正弦定理可得2sin AsinBcosBsinBsinA0 ， 1 2π 又因为A,B 0,π ，则sin A,sinB 0，可得2cosB10，即cosB  ，所以B  ， 2 3 由余弦定理可得b2 a2 c2 2accosB3ac123acac 4， 1 1 3 所以ABC面积的最大值为 acsinB  4  3 .故选：C. 2 2 2 试卷第1页，共8页 {#{QQABBQAAgggAAhBAAQhCEQUoCgKQkACCAaoGRFAYMAIAiRFABCA=}#}8．A【解析】设函数 f  x 的最小正周期为T .    因为函数 f  x 在  ， 上单调递增，    12 12 T     则  ( ) ，可得T  ,又0，所以，06， 2 12 12 6 3 π 因为函数 f  x 的图象向左平移 个单位之后与 f  x 的图象关于x轴对称. 2  2n1  T  2n1  π 则    nN ，即4n2  nN ， 2  2 因为06，所以2或6，2满足条件，A正确 二、选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合 题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分. 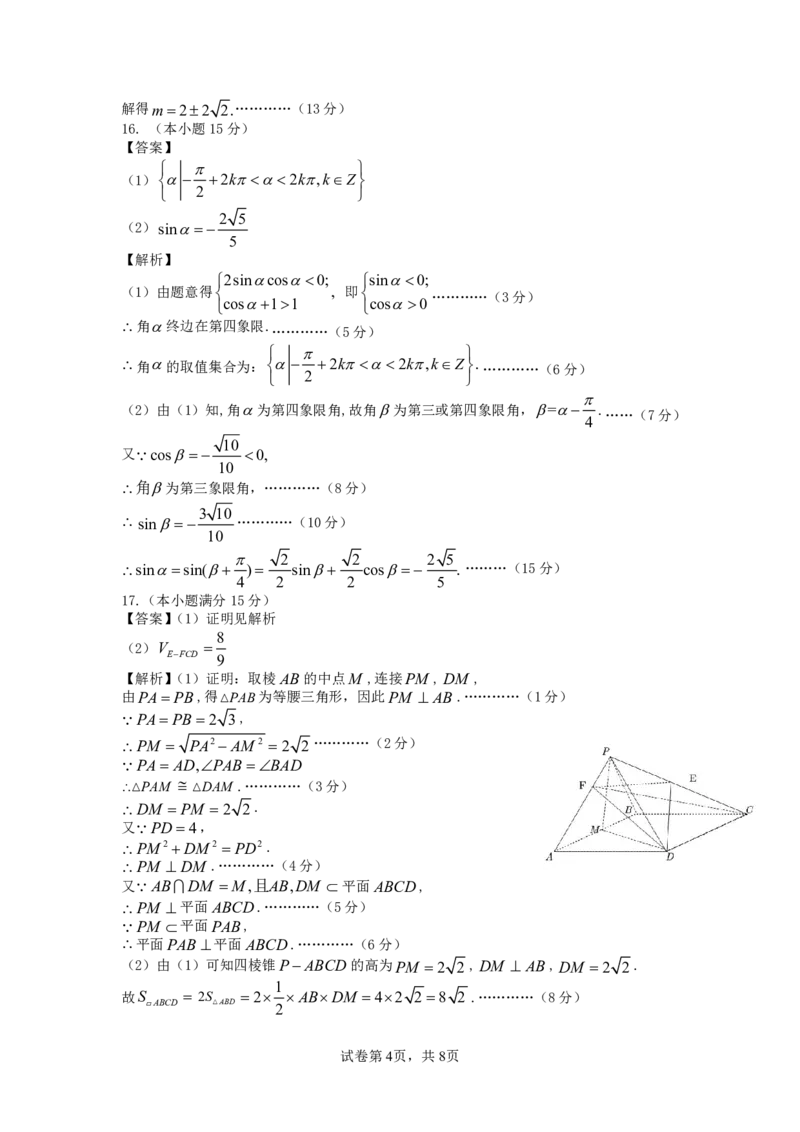9.BCD【解析】对于B：如图过D作DE OB交OB于点E， 由AD 2，CD2，得AD 2 2，故B正确； 对于A：还原平面图如下图， 则 AB  AB 4,CD CD 2,AD  2AD 2 2 ，故A错误； 对于C：过C作CF  AB交AB于点F ，则AF  DC  2， 由勾股定理得，CB  22 (2 2)2 2 3 故四边形ABCD的周长为：422 22 3 62 22 3 ，即C正确； 1 对于D：四边形ABCD的面积为：  42 2 2 6 2 ，即D正确.故选：BCD. 2 10．AD【解析】对于A，由A B，可得a b，由正弦定理可得sinAsinB，所以A正确； 对于B，由正弦定理得a2 b2 c2，所以C为锐角，但不能断定ABC是否为锐角三角形， 故B错误； 对于C，因为A、B 0,π ，则2A、2B 0,2π ， 因为sin2Asin2B，所以2A2B或2A2B  π或2A2B 3π， π 若2A2B，则A B；若2A2B  π，则AB  ； 2 3π 若2A2B 3π，则AB  ，这与ABC的内角和定理矛盾. 2 综上所述，ABC为等腰或直角三角形，C错； 1  1 1 对于D，若ABC面积为S ，因为S  a2b2c2 ，则 absinC  2abcosC ， 4 2 4 sinC π 所以sinC cosC ，则tanC  1，由于C 0,π ，则C  ，故D正确；故选： cosC 4 AD. 11．ACD【解析】对于A，g  f  x  cos  sinx ，其定义域为R 且关于原点对称， g(f(x))cos(sin(x))cos(sinx)cos(sinx) g(f(x)) ，即g(f(x))为偶函数， 故A正确； 对于B, f  g  x  sin  cosx ，其定义域为R 且关于原点对称， f  g x  sin  cos x  sin  cosx  f  g  x  ，即 f  g  x  为偶函数，故B错误；  对于C，令g(f(x))0,即cos(sinx)0,即sinx k ，kZ ， 2 试卷第2页，共8页 {#{QQABBQAAgggAAhBAAQhCEQUoCgKQkACCAaoGRFAYMAIAiRFABCA=}#}又1sinx1，所以g  f  x  在R上没有零点，故C正确 对于D， f(g(x))sin(cosx)，因为 sin(cosx) sin(cos(x2)),即f(g(x2))  f(g(x)) ， 假设存在0T 2，使得sin(cosx) sin(cos(xT)) 对任意的xR恒成立， 令x0，则sin1sin(cos(T))，所以cos(T)1，即T 2k,kZ ， 因为0T 2，这样的T 不存在， 所以 f  g  x  的最小正周期为2，故D正确；故选：ACD 三、填空题：本题共3小题，每小题5分，共15分.  1 9 9      12.  ，  ，  【解析】因为a (3,1)，b (2,3)，a，b的夹角为锐角，  2 2 2  1 9 所以630且29 ，解得 且 ， 2 2  1 9 9  即的取值范围是  ，  ， ，  2 2 2  2 1 1 13． 【解析】由sin() ，可得sincoscossin ， 3 3 3 tan sin sin 由 3可得： 3 ，即sincos3cossin0， tan cos cos 1 1 1 1 2 联立可得：cossin ,sincos ，所以sincoscossin   ， 6 2 2 6 3 14.28 3【解析】正四面体的棱长为6，从各棱的三等分点处截得多面体， 则该多面体的棱长为2，且表面由四个正三角形和四个正六边形组成， 1 1 故该多面体的表面积为4 2 346 2 3 28 3 ，故答案为：28 3. 2 2 四、解答题：本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤. 15.（本小题13分） 【答案】 3 5 （1） z  .； 1 2 （2）m22 2. 【解析】 (1)z z  m3i  2i   2m3  m6  i.…………（1分） 1 2 z z 为纯虚数， 1 2 2m30; 3  ,解得m ,…………（3分） m60 2 3 9 3 5 z  3i, z  9  .…………（5分） 1 2 1 4 2 （2）由题意得A  m,3 ，B  2,1 ,C  m,3 .…………（7分） VABC为直角三角形， AB BC.…………（9分）   ABBC  0.即 2m,2  m2,4 0.…………（11分） 试卷第3页，共8页 {#{QQABBQAAgggAAhBAAQhCEQUoCgKQkACCAaoGRFAYMAIAiRFABCA=}#}解得m22 2.…………（13分） 16. （本小题15分） 【答案】    （1） 2k2k,kZ  2  2 5 （2）sin 5 【解析】 2sincos0; sin0; （1）由题意得 , 即 …………（3分） cos11 cos0 角终边在第四象限. …………（5分）    角的取值集合为： 2k 2k,kZ. …………（6分）  2   （2）由（1）知,角为第四象限角,故角为第三或第四象限角，= . ……（7分） 4 10 又cos 0, 10 角为第三象限角，…………（8分） 3 10  sin …………（10分） 10  2 2 2 5 sinsin( ) sin cos . 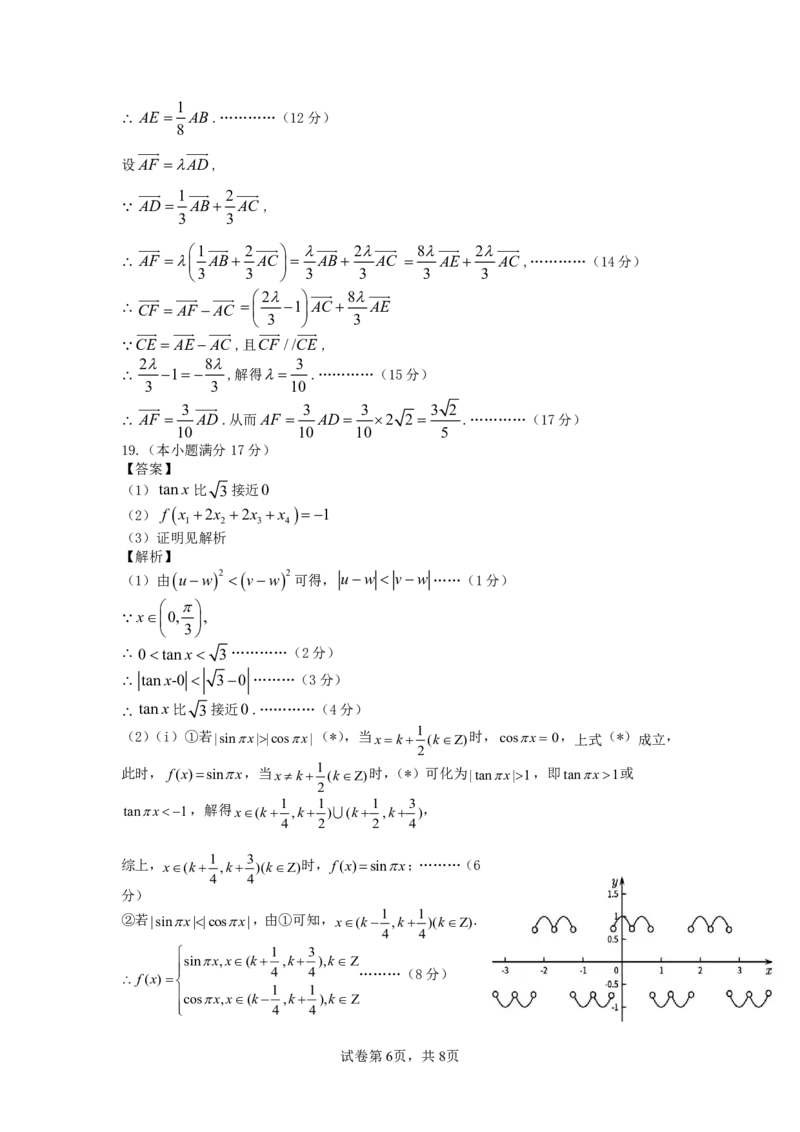………（15分） 4 2 2 5 17.（本小题满分15分） 【答案】（1）证明见解析 8 （2）V  EFCD 9 【解析】（1）证明：取棱AB的中点M ,连接PM ,DM , 由PA PB,得VPAB为等腰三角形，因此PM  AB.…………（1分） PA PB  2 3, PM  PA2 AM2  2 2 …………（2分） PA AD,PAB BAD VPAM  VDAM .…………（3分） DM  PM  2 2. 又PD 4， PM2DM2  PD2 . PM  DM .…………（4分） 又ABDM M,且AB,DM  平面ABCD, PM 平面ABCD.…………（5分） PM 平面PAB, 平面PAB 平面ABCD.…………（6分） （2）由（1）可知四棱锥PABCD的高为PM 2 2 ,DM  AB,DM 2 2 . 1 故S  2S 2 ABDM 42 2 8 2 .…………（8分） ABCD VABD 2 试卷第4页，共8页 {#{QQABBQAAgggAAhBAAQhCEQUoCgKQkACCAaoGRFAYMAIAiRFABCA=}#}E为PC的中点， S  2S …………（10分） PCD ECD AF 2FP, 1 F到平面PCD的距离为A到平面PCD距离的 .…………（12分） 3 1 1 1 1 1 1 V V  V  V  V  V   8 22 2 EFCD FECD 3 AECD 6 APCD 6 PACD 12 PABCD 12 3 8  .…………（15分） 9 18.（本小题满分17分） 【答案】     1 2 （1）BC  ACAB ，AD  AB AC 3 3 10 （2）cosBAC  10 3 2 （3）AF  5    【解析】BC  ACAB ,…………（2分）     2  2    1 2 AD  ABBD  AB BC  AB AC AB  AB AC .…………（4分） 3 3 3 3  1 2 （2）解法一：由（1）得AD  AB AC， 3 3   2 1 2 2 则有 AD   AB AC ，…………（6分） 3 3   2 1  2 4  2 4   即 AD = AB  AC  AB AC cosBAC 9 9 9 16 40 4 8   4 10cosBAC………（8分） 9 9 9 10 解得cosBAC  ，…………（10分） 10 解法二：设CD  x，则BC 3x， cosACD cosACB 由余弦定理可得： AC2 CD2 AD2 AC2 BC2 AB2  …………（6分） 2ACCD 2ACBC 10x2 8 109x2 16 即  , 2 10x 2 103x 解得x 2，可得CD  2,BC 3 2 .…………（8分） AB2 AC2 BC2 161018 10 cosBAC    ,.…………（10分） 2ABAC 24 10 10            2 （3）设 EA t,则EAEC  EA EA AC  EA EAAC t2 t 1  1   1 当t  ,即 EA  时,EAEC 取得最小值 . 2 2 4 试卷第5页，共8页 {#{QQABBQAAgggAAhBAAQhCEQUoCgKQkACCAaoGRFAYMAIAiRFABCA=}#}1  AE  AB .…………（12分） 8   设AF AD,  1 2  AD  AB AC , 3 3  1 2  2 8 2  AF   AB AC  AB AC  AE AC ,…………（14分） 3 3  3 3 3 3    2  8  CF  AF AC   1AC AE  3  3      CE  AEAC ,且CF //CE , 2 8 3  1 ,解得 .…………（15分） 3 3 10  3  3 3 3 2  AF  AD.从而AF  AD  2 2 .…………（17分） 10 10 10 5 19.（本小题满分17分） 【答案】 （1）tanx比 3接近0 （2） f  x 2x 2x x 1 1 2 3 4 （3）证明见解析 【解析】 （1）由 uw 2  vw 2可得， uw  vw ……（1分）   x 0, ,  3  0tanx 3 …………（2分）  tanx-0  30 ………（3分） tanx比 3接近0.…………（4分） 1 （2）（i）①若|sinx||cosx|（*），当 xk (kZ) 时，cosx0，上式（*）成立， 2 1 此时， f(x)sinx，当 xk (kZ) 时，（*）可化为|tanx|1，即tanx1或 2 1 1 1 3 tanx1，解得 x(k ,k )(k ,k ) ， 4 2 2 4 1 3 综上， x(k ,k )(kZ) 时，f(x)sinx；………（6 4 4 分） 1 1 ②若|sinx||cosx|，由①可知， x(k ,k )(kZ) . 4 4  1 3 sinx,x(k ,k ),kZ   4 4 ………（8分） f(x)  cosx,x(k 1 ,k 1 ),kZ  4 4 试卷第6页，共8页 {#{QQABBQAAgggAAhBAAQhCEQUoCgKQkACCAaoGRFAYMAIAiRFABCA=}#}作出函数图像如图所示， 3 3 1 当  x 且x 时，关于x的方程 f  x a0有且仅有4个不相等的实数根 4 4 4 x ,x ,x ,x ,且x  x  x  x ， 1 2 3 4 1 2 3 4 3 3 1 当  x 且x 时， y  f (x)与 y a有且仅有四个公共点. 4 4 4 1 由对称性可知，x x 0，x x  ，x x 1.………（9分） 1 2 2 3 2 3 4 3 3  f  x 2x 2x x  f   sin 1…………（10分） 1 2 3 4 2 2    （ii）由 PM PN  MN 可得MP  NP.……（11分） 1 1 ①当x(k ,k ),(kZ) 时，设P  x,cosx . 4 4    8 M  5,4 , N 5,   3      8 MP x 5,cosx4 ,NP  x 5,cosx .  3   MP  NP,     8  x 5 x 5  cosx4  cosx  0 .……（12分）  3 2  10 49 即cosx  x2 （*）.……（13分）  3  9 cosx1， 2  10 49  cosx    3  9 49 49 又x2   ， 9 9  2  10 49 cosx  = ; 当且仅当    3  9 时，（*）式成立，解得x0  49 49 x2     9 9 1 1 当x(k ,k ),(kZ) 时，存在唯一的P  0,1  ,使得（*）式成立..……（14分） 4 4 1 3 ②当x(k ,k ),(kZ)时，设P  x,sinx ， 4 4 2  10 49 同理可得sinx  x2 （#）……（15分）  3  9 sinx1 ， 2  10 49  sinx    3  9 试卷第7页，共8页 {#{QQABBQAAgggAAhBAAQhCEQUoCgKQkACCAaoGRFAYMAIAiRFABCA=}#}49 49 又x2   ， 9 9  2  10 49 sinx  = ; 当且仅当    3  9 时，（#）式成立，  49 49 x2     9 9 但两个方程无法同时成立， 1 3 当x(k ,k ),(kZ)时,不存在满足题意的P点..……（16分） 4 4    综上所述， f  x 的图象上存在唯一的点P  0,1  ,使得 PM PN  MN .……（17分） 试卷第8页，共8页 {#{QQABBQAAgggAAhBAAQhCEQUoCgKQkACCAaoGRFAYMAIAiRFABCA=}#}