文档内容
高一数学期中模拟试题
(B 能力卷)
班级_______ 姓名________ 考号_________
一、单项选择题(本大题共8题,每小题5分,共计40分。每小题列出的四个选项中只有一
项是最符合题目要求的)
1.复数 的虚部是( )
A. B. C. D.
2.设向量 , ,若 则实数 的值是( )
A. B.1 C.2 D.3
3.已知 是单位向量, 与 的夹角是 ,且 , 则 =( )
A. B. C. D.
4.已知平面 与平面 交于直线 ,且直线 ,直线 ,且直线 , , 不重合,则下列命题错
误的是( )
A.若 , ,且 与 不垂直,则
B.若 , ,则
C.若 , ,且 与 不平行,则
D.若 , ,则
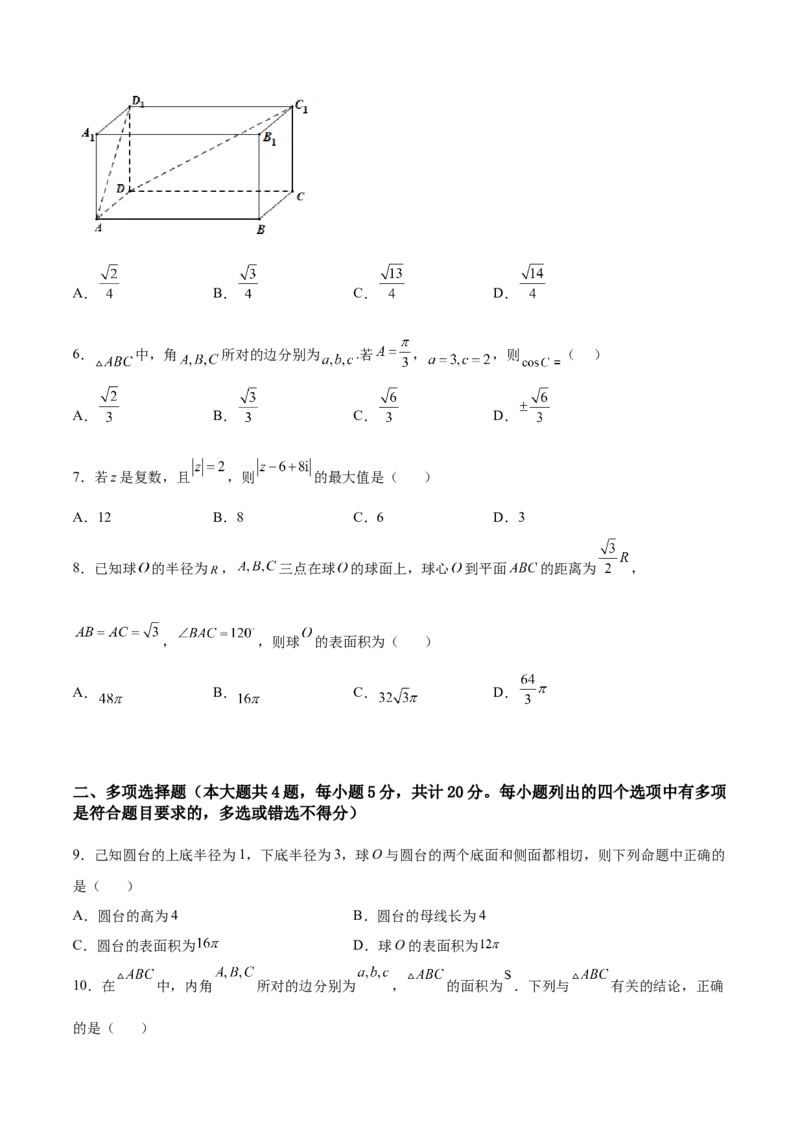
5.在长方体 中, , ,则异面直线 与 所成角的正弦值
是( )A. B. C. D.
6. 中,角 所对的边分别为 .若 , ,则 ( )
A. B. C. D.
7.若z是复数,且 ,则 的最大值是( )
A.12 B.8 C.6 D.3
8.已知球 的半径为 , 三点在球 的球面上,球心 到平面 的距离为 ,
, ,则球 的表面积为( )
A. B. C. D.
二、多项选择题(本大题共4题,每小题5分,共计20分。每小题列出的四个选项中有多项
是符合题目要求的,多选或错选不得分)
9.己知圆台的上底半径为1,下底半径为3,球O与圆台的两个底面和侧面都相切,则下列命题中正确的
是( )
A.圆台的高为4 B.圆台的母线长为4
C.圆台的表面积为 D.球O的表面积为
10.在 中,内角 所对的边分别为 , 的面积为 .下列与 有关的结论,正确
的是( )A.若 , , ,则 或
B.若 为锐角三角形,则
C.若 为 的外接圆半径,则
D.若 , ,则 是直角三角形
11.已知向量 ,下列结论正确的是( )
A. 与 能作为一组基底
B.与 同向的单位向量的坐标为
C. 与 的夹角的正弦值为
D.若 满足 ,则
12.在正六棱锥 中,已知底面边长为1,侧棱长为2,则( )
A.
B.共有4条棱所在的直线与AB是异面直线
C.该正六棱锥的内切球的半径为
D.该正六棱锥的外接球的表面积为
三、填空题(每小题5分,共计20分)
13.已知复数 为纯虚数,则实数 ______.
14.已知平面向量 , 的夹角为 ,且 , ,则 ______.
15.如图,在 ABC中,点D在边AB上,CD垂直于BC,∠A=30°,BD=2AD, ,则 ABC的
△ △
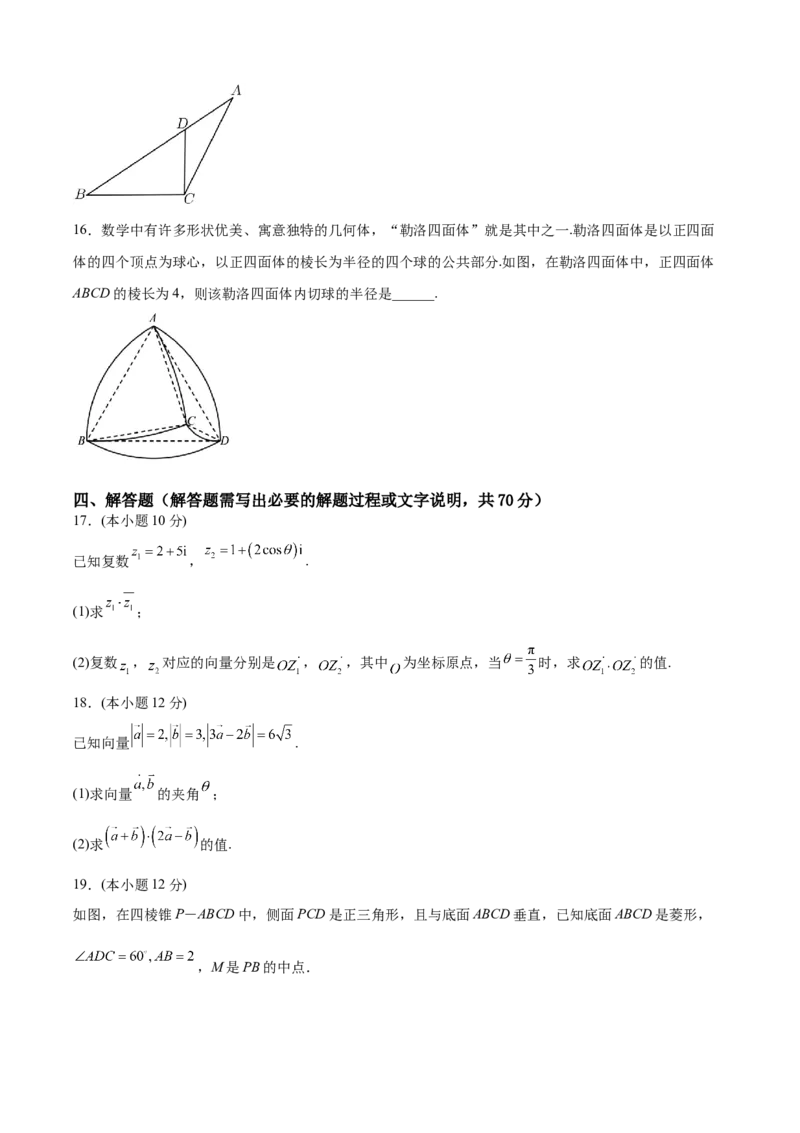
面积为______.16.数学中有许多形状优美、寓意独特的几何体,“勒洛四面体”就是其中之一.勒洛四面体是以正四面
体的四个顶点为球心,以正四面体的棱长为半径的四个球的公共部分.如图,在勒洛四面体中,正四面体
ABCD的棱长为4,则该勒洛四面体内切球的半径是______.
四、解答题(解答题需写出必要的解题过程或文字说明,共70分)
17.(本小题10分)
已知复数 , .
(1)求 ;
(2)复数 , 对应的向量分别是 , ,其中 为坐标原点,当 时,求 的值.
18.(本小题12分)
已知向量 .
(1)求向量 的夹角 ;
(2)求 的值.
19.(本小题12分)
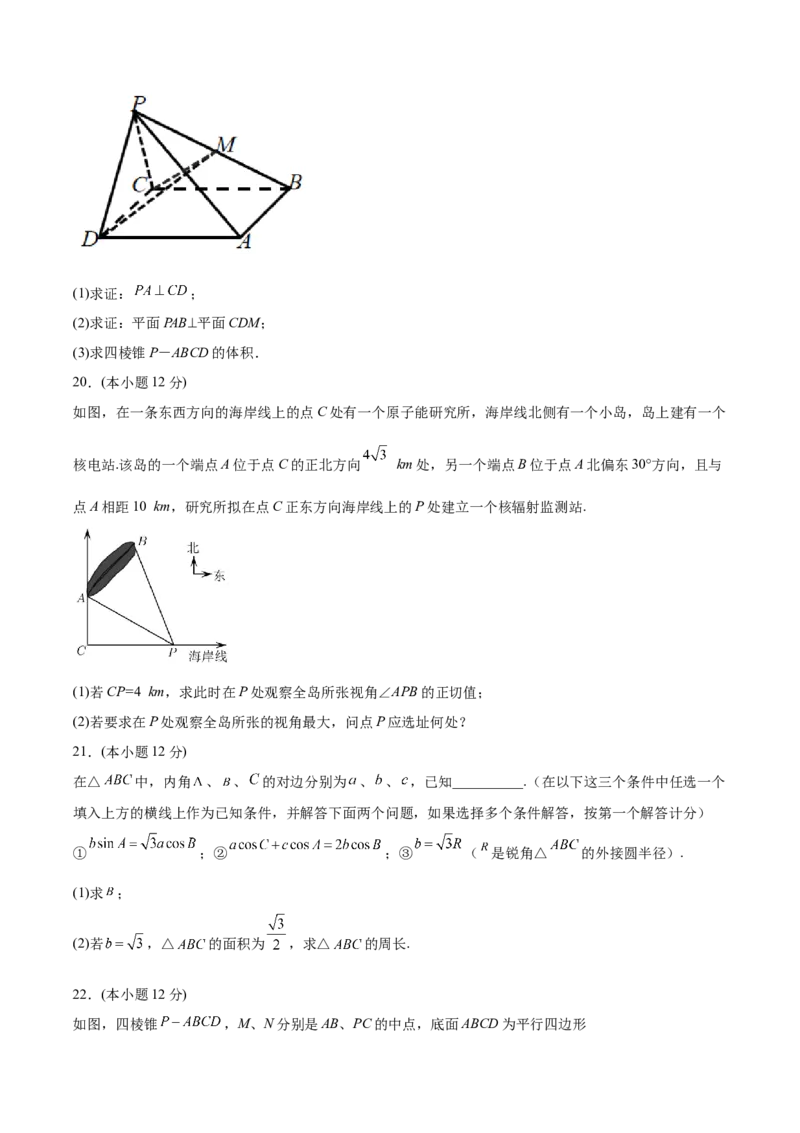
如图,在四棱锥P-ABCD中,侧面PCD是正三角形,且与底面ABCD垂直,已知底面ABCD是菱形,
,M是PB的中点.(1)求证: ;
(2)求证:平面PAB⊥平面CDM;
(3)求四棱锥P-ABCD的体积.
20.(本小题12分)
如图,在一条东西方向的海岸线上的点C处有一个原子能研究所,海岸线北侧有一个小岛,岛上建有一个
核电站.该岛的一个端点A位于点C的正北方向 km处,另一个端点B位于点A北偏东30°方向,且与
点A相距10 km,研究所拟在点C正东方向海岸线上的P处建立一个核辐射监测站.
(1)若CP=4 km,求此时在P处观察全岛所张视角∠APB的正切值;
(2)若要求在P处观察全岛所张的视角最大,问点P应选址何处?
21.(本小题12分)
在△ 中,内角 、 、 的对边分别为 、 、 ,已知__________.(在以下这三个条件中任选一个
填入上方的横线上作为已知条件,并解答下面两个问题,如果选择多个条件解答,按第一个解答计分)
① ;② ;③ ( 是锐角△ 的外接圆半径).
(1)求 ;
(2)若 ,△ 的面积为 ,求△ 的周长.
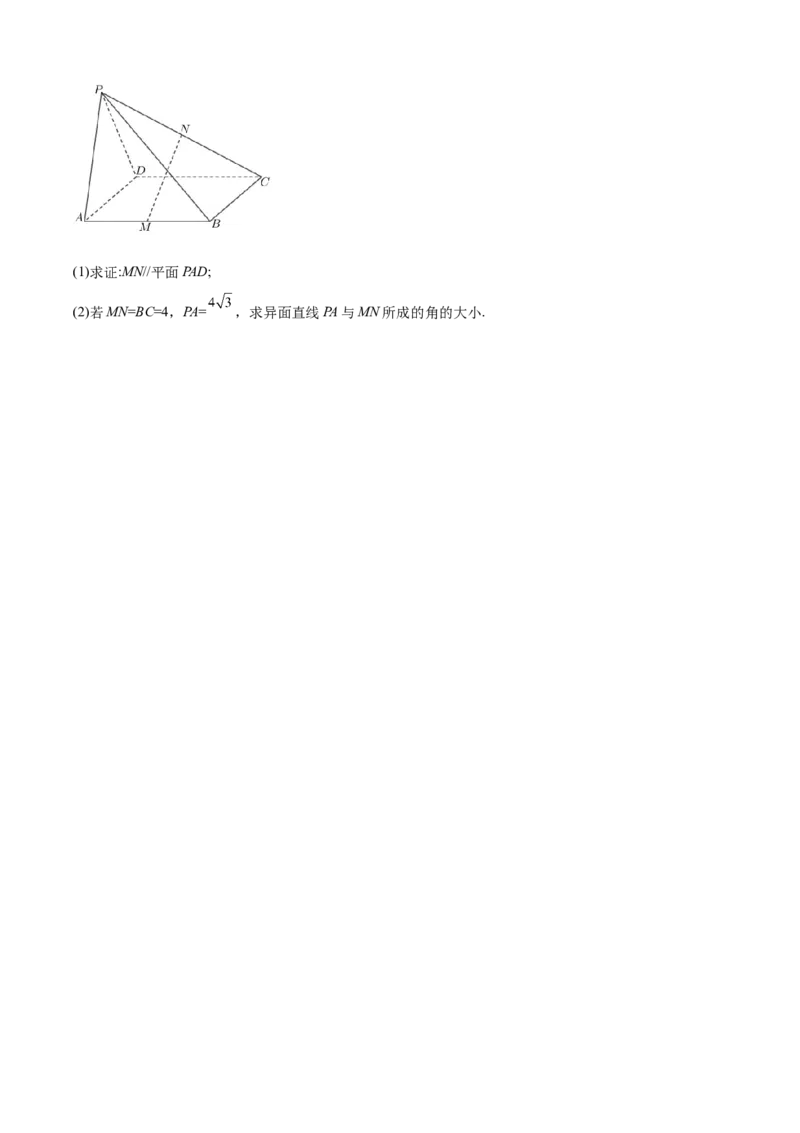
22.(本小题12分)
如图,四棱锥 ,M、N分别是AB、PC的中点,底面ABCD为平行四边形(1)求证:MN//平面PAD;
(2)若MN=BC=4,PA= ,求异面直线PA与MN所成的角的大小.