文档内容
期末模拟卷
(A 基础卷)
班级______ 姓名_______ 考号______
一、单项选择题(本大题共8题,每小题5分,共计40分。每小题列出的四个选项中只有一
项是最符合题目要求的)
1.复数 ( 为虚数单位)的虚部为( )
A. B.1 C. D.
【答案】A
【详解】
复数 的虚部是 .
故选:A
2.已知向量 ,那么向量 的坐标是( )
A. B. C. D.
【答案】D
【详解】
解:因为 ,所以 ;
故选:D
3. , 是两个不同的平面, , 是两条不同的直线,下列命题中正确的是( )
A.如果 , , , 是异面直线,那么
B.若 , , ,则
C.若 , ,则
D.如果 , , , 共面,那么
【答案】B
【详解】
对于A:如果 , , , 是异面直线,那么 或 与 相交,A不正确;
对于B:若 ,则 ,使得
,则 ,使得
∴
∵ ,则
B正确;
对于C:若 , ,则 , 的位置关系为:平行或相交,C不正确;对于D:如果 , , , 共面,则 , 的位置关系:相交或平行,D不正确;
故选:B.
4.甲、乙两人玩猜数字游戏,先由甲心中想一个数字,记为a,再由乙猜甲刚才所想的数字,把乙猜的
数字记为b,其中 ,则“a=b”的概率为( )
A. B. C. D.
【答案】C
【详解】
解:甲乙猜数字时互不影响,故各有5种可能,故基本事件是 种,
则“a=b”的基本事件有: ,故5种,
所以“a=b”的概率为 ,
故选:C
5.在 中,已知 ,且 ,则 ( )
A. B. C. D.
【答案】D
【详解】
解:在 中,因为 ,即 ,
所以由正弦定理得: ,
因为 ,所以 ,
所以 ,
所以 ,
故选:D
6.已知 ,向量 在向量 上的投影向量的模为 ,则 与 的夹角可以为( )
A. B. C. D.
【答案】B
【详解】
解:记向量 与向量 的夹角为 , ,
而 ,在 上的投影为 ,
在 上的投影为 , ,
,
,
.
故选:B.
7.某中学从甲、乙两个班中各选出7名学生参加2022年“希望杯”全国数学邀请赛,他们取得成绩的茎
叶图如图,其中甲班学生成绩的中位数是84,乙班学生成绩的平均数是86,则xy的值为( )
A.36 B.12 C.10 D.24
【答案】D
【详解】
因为甲班学生成绩的中位数是84,
所以根据茎叶图可得 为中位数,
即 ,
解得 .
又因为乙班学生成绩的平均数是86,
即 ,
解得 ,
故 .
故选:D.
8.中国古代数学名著《九章算术》的商功章记载了圆锥型几何体的体积公式,“水曰:下周自乘,以高
乘之三十六而一”,其意思是:已知圆锥的底面周长C,高h,那么圆锥的体积公式是 ,若一
圆锥的轴截面是边长为 的等边三角形,据依所给公式计算其体积为( )
A. B. C. D.
【答案】C
【详解】因为圆锥的轴截面是边长为 的等边三角形,
所以其底面直径 ,周长为 ,高 ,
故其体积为 .
故选:C
二、多项选择题(本大题共4题,每小题5分,共计20分。每小题列出的四个选项中有多项
是符合题目要求的,多选或错选不得分)
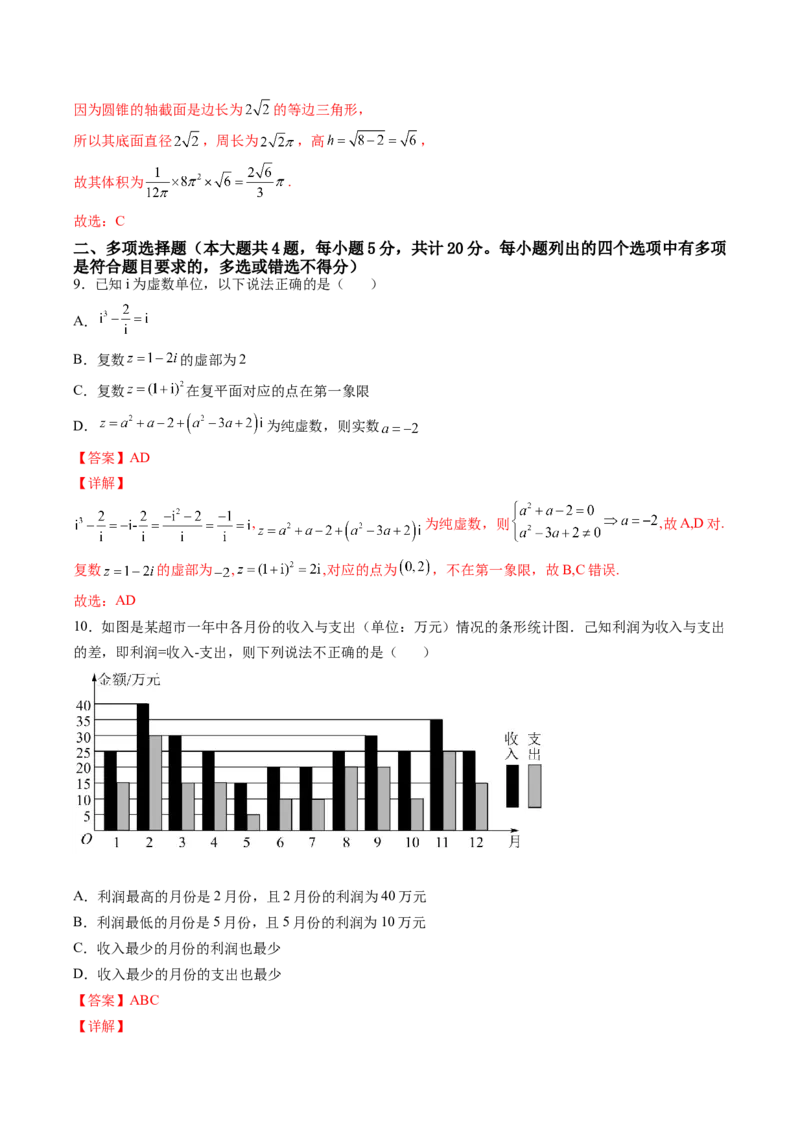
9.已知i为虚数单位,以下说法正确的是( )
A.
B.复数 的虚部为2
C.复数 在复平面对应的点在第一象限
D. 为纯虚数,则实数
【答案】AD
【详解】
, 为纯虚数,则 ,故A,D对.
复数 的虚部为 , ,对应的点为 ,不在第一象限,故B,C错误.
故选:AD
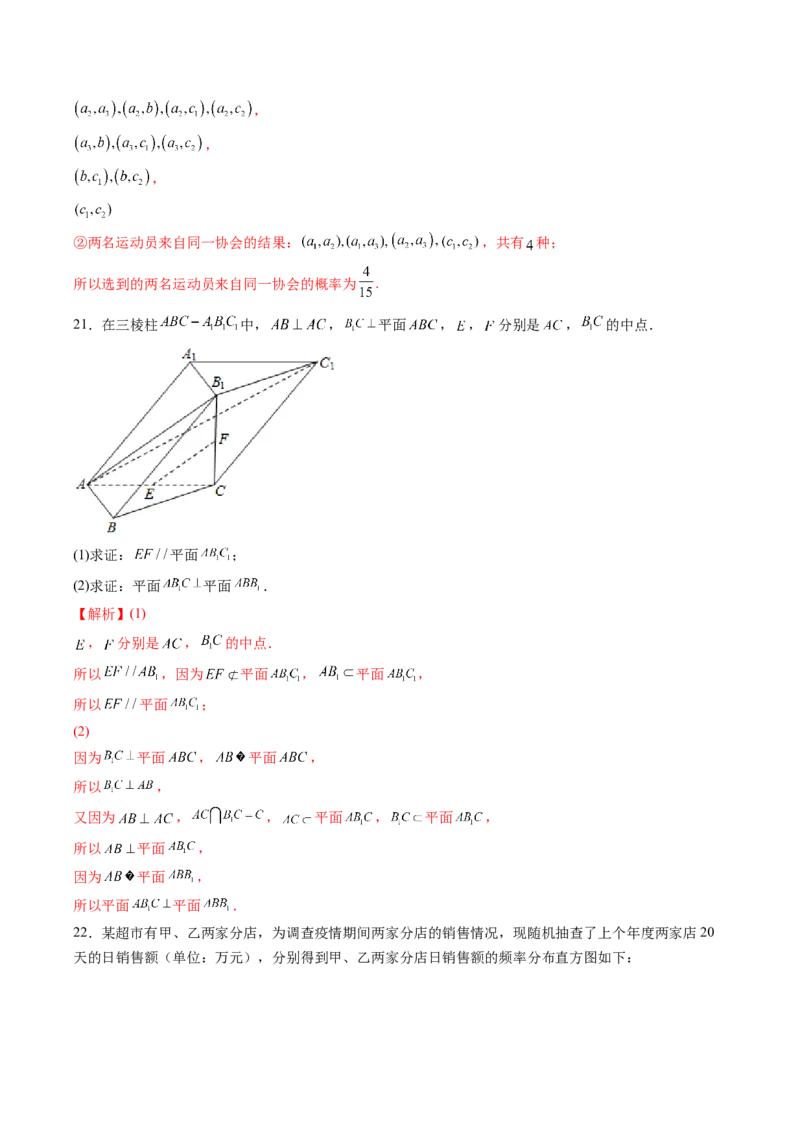
10.如图是某超市一年中各月份的收入与支出(单位:万元)情况的条形统计图.己知利润为收入与支出
的差,即利润=收入-支出,则下列说法不正确的是( )
A.利润最高的月份是2月份,且2月份的利润为40万元
B.利润最低的月份是5月份,且5月份的利润为10万元
C.收入最少的月份的利润也最少
D.收入最少的月份的支出也最少
【答案】ABC
【详解】在A中,利润最高的月份是3或10月份,且3或10月份的利润为15万元,故A错误;
在B中,利润最小的月份是8月份,且8月分的利润为5万元,故B错误;
在C中,收入最少的月份是5月份,但5月份的支出也最少,故5月分的利润不是最少,故C错误;
在D中,收入最少的月份是5月份,但5月份的支出也最少,故D正确.
故选:ABC.
11.从一批准备出厂的电视机中随机抽取10台进行质量检查,其中有1台是次品,若用C表示抽到次品
这一事件.则下列说法中不正确的是( )
A.事件C发生的概率为 B.事件C发生的频率为
C.事件C发生的概率接近 D.每抽10台电视机,必有1台次品
【答案】ACD
【详解】
事件C发生的频率为 ,由于只做了一次实验,故不能得到概率为 或概率接近 ;
当然每抽10台电视机,必有1台次品也不一定发生.
故B正确,ACD错误.
故选:ACD
12.如图所示,在正方体 中,O为DB的中点,直线 交平面 于点M,则下列结
论正确的是( )
A. ,M,O三点共线 B. 平面
C.直线 与平面 所成角的为 D.直线 和直线 是共面直线
【答案】ABC
【详解】
由正方体的特性可知, 为正方体 的体对角线, 平面 ,平面 平
面 于 ,又 交平面 于点 ,故点 在 上,故A项正确;
由正方体的特性可知, 平面 , 平面 ,故 ,同理, ,
于点 ,故 平面 ,故B项正确;
设正方体的边长为1,直线 与平面 的夹角为 ,则 ,点 到平面 的距离为,故 , ,C项正确;
直线 与直线 为异面直线,故D项错误.
故选:ABC.
三、填空题(每小题5分,共计20分)
13.在 中, ,若 ,则 的大小是___________.
【答案】 ##
【详解】
由余弦定理可得
整理得 ,即
由 ,所以 为等边三角形
所以 .
故答案为:
14.已知 与 夹角 求 在 方向上的投影____________.
【答案】1
【详解】
因为 与 夹角 ,
所以 在 方向上的投影为 ,
故答案为:1.
15.把一个正方体的表面涂上红色,在它的长、宽、高上等距离地各切三刀,则大正方体被分割成了
个大小相等的小正方体,将这些小正方体均匀地搅混在一起.如果你从这些小正方体中随意地取出 个,则
这个小正方体至少有一个面涂有红色的概率为_______.
【答案】 ##
【详解】个小正方体中,将大正方体外层的正方体去掉,可知没有面是红色的小正方体有 个,
至少有一个面涂有红色的概率为 .
故答案为: .
16.某歌舞厅的迪斯科球体积为 (立方米),其表面上有A,B,C,D四点构成一等腰梯形,
, ,则该迪斯科球的球心到面ABCD的距离为__________米.
【答案】
【详解】
解:由题意得:
设球的半径为R,由球的体积公式可得 ,即 ,故 .
取BC中点F,易证FB=FD=BA=FC=2.
同理FA=FD=2
∴F是梯形ABCD外接圆圆心,其半径r=2.
∴球心到面的距离 .
故答案为:四、解答题(解答题需写出必要的解题过程或文字说明,共70分)
17.设复数 (其中 ), .
(1)若 是纯虚数,求 ;
(2)求满足 的复数 在复平面上对应的点构成的图形的面积.
【答案】(1) (2)
【解析】(1)
依题意 且 ,
所以
(2)
设 ,则
故复数 在复平面上对应的点构成的图形是以 为圆心,半径为 的圆及其内部
所以
18.已知平面向量 , 满足: , , .
(1)求 与 的夹角 ;
(2)求向量 在向量 上的投影.
【答案】(1) (2)
【解析】(1)
∵ ,∴ ,
又∵ ,∴ ,∴ .
∵ ,∴ .
(2)
∵ ,∴ ,∴向量 在向量 上的投影为 .
19.在 ABC中,内角A、B、C的对边分别为a、b、c,且 .
△
(1)求角C的大小;
(2)如果 , ,求c的值.
【答案】(1) (2)
【解析】(1)
由 得 ,
由正弦定理可得 ,
因为 ,所以 ,即 ,
因为 ,所以 .
(2)
因为 ,所以 ,
所以 ,所以 .
20.设甲、乙、丙三个乒乓球协会的运动员人数分别为 、9、 ,现用分层抽样的方法从三个协会中抽
取 名运动员参加比赛.
(1)求应从这三个协会中分别抽取的运动员人数;
(2)现从这6名运动员中随机抽取2名参加双打比赛.
①列出所有可能的结果;
②求选到的两名运动员来自同一协会的概率.
【答案】(1)甲、乙、丙三个乒乓球协会分别抽取运动员人数为 、 、
(2)①答案见解析,②
【解析】(2)
设甲乒乓球协会分别抽取的 名运动员编号为 ,
乙乒乓球协会分别抽取的1名运动员编号为 ,
丙乒乓球协会分别抽取的 名运动员编号为 ,
①选出两人共有15种结果,
,,
,
,
②两名运动员来自同一协会的结果: ,共有 种;
所以选到的两名运动员来自同一协会的概率为 .
21.在三棱柱 中, , 平面 , , 分别是 , 的中点.
(1)求证: 平面 ;
(2)求证:平面 平面 .
【解析】(1)
, 分别是 , 的中点.
所以 ,因为 平面 , 平面 ,
所以 平面 ;
(2)
因为 平面 , 平面 ,
所以 ,
又因为 , , 平面 , 平面 ,
所以 平面 ,
因为 平面 ,
所以平面 平面 .
22.某超市有甲、乙两家分店,为调查疫情期间两家分店的销售情况,现随机抽查了上个年度两家店20
天的日销售额(单位:万元),分别得到甲、乙两家分店日销售额的频率分布直方图如下:(1)比较甲乙两店日销售额的平均数的大小(同一组中的数据用该组区间的中点值作代表):
(2)若规定分店一年(按360天计算)中日销售额不低于55万的天数不少于120天为运转良好,请结合上
图,分析甲店上个年度运转是否良好?
(3)如果你是投资决策者,你更愿意在哪家店投资,请你根据所学的统计知识,说明你的理由.(不需要
计算,只需要说清楚理由)
【答案】(1) (2)甲店运转良好(3)我选乙店,理由见解析
【解析】
【详解】
(1)解:估计算甲店的日销售额平均数为
估计算乙店的日销售额平均数为
.
.
(2)解:日销售额超过55万的天数占比不少于 ,
甲日销售额不低于55万的概率约为 ,
甲店运转良好.
(3)解:答案一:甲店日销售额平均值略高于乙店,由频率分布直方图可知.甲店的销售额方差明显低
于乙店,故甲店销售情况比乙店要稳定,所以我选甲店;
答案二:虽然甲店日销售额平均值略高于乙店,但乙店日销售额在80万-100万出现的概率比甲店高,故
我认为乙店更有潜力,所以我选乙店.