文档内容
第六章 平面向量及其应用B(提高卷)
参考答案与试题解析
一.选择题(共8小题)
1.(2019秋•长宁区期末)设 为两个非零向量 、 的夹角,已知当实数t变化时 的最小值为2,
θ
则( )
A.若 确定,则 唯一确定 B.若 确定,则 唯一确定
θ θ
C.若 确定,则 唯一确定 D.若 确定,则 唯一确定
θ θ
【解答】解:令f(t) 2 2t t2 ;
∴△=4( • )2﹣4 • 4 • (cos ﹣1)≤0恒成立,
θ
当且仅当t cos 时,f(t)取得最小值2,
θ
∴( cos )2 2( cos )• • 2,
θ θ
化简 sin2 =2.
∴ 确定,则θ| |唯一确定
故θ选:A.
2.(2020春•常州期中)在△ABC中,内角A、B、C所对边分别为a、b、c,若 ,
则∠B的大小是( )
A. B. C. D.
【解答】解:由正弦定理可知,a=2RsinA,b=2RsinB,c=2RsinC,(R为三角形外接圆半径),
因为 ,
所以, ,且A,B,C都为锐角,
所以 ,所以﹣tanB=tan(A+C) ,
整理可得,tan2B=3,
故tanB ,B .
故选:D.
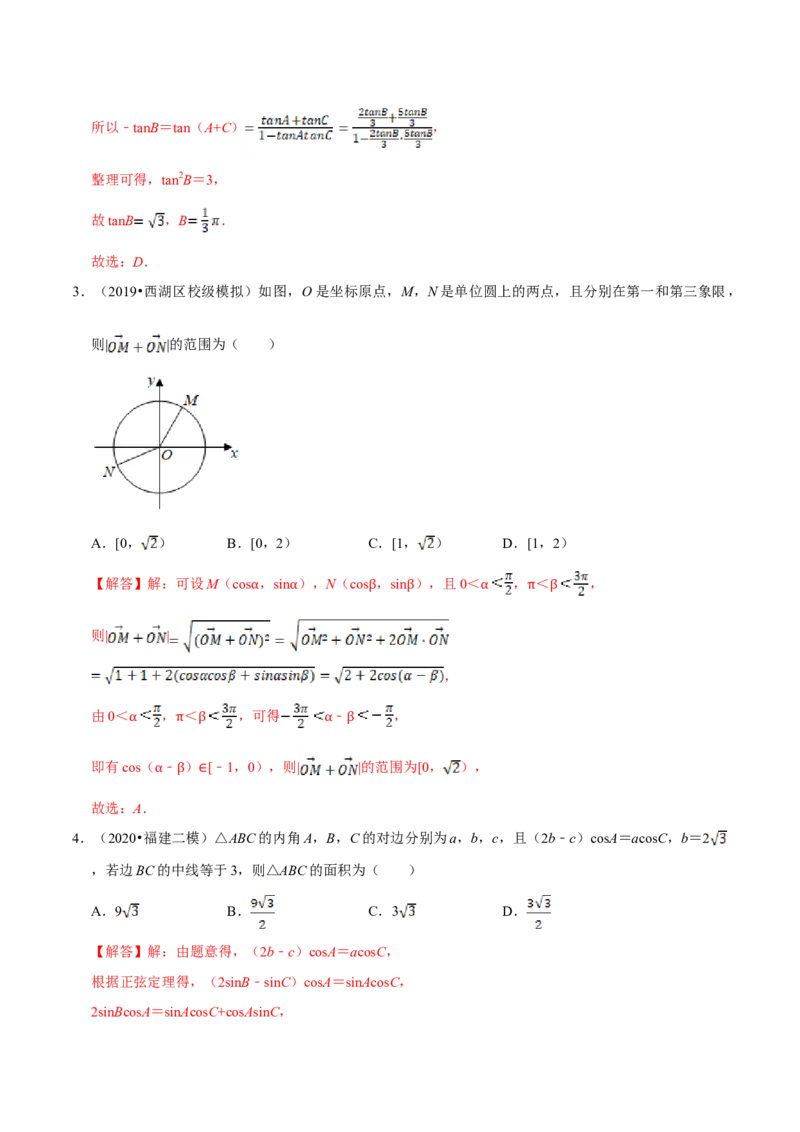
3.(2019•西湖区校级模拟)如图,O是坐标原点,M,N是单位圆上的两点,且分别在第一和第三象限,
则| |的范围为( )
A.[0, ) B.[0,2) C.[1, ) D.[1,2)
【解答】解:可设M(cos ,sin ),N(cos ,sin ),且0< , < ,
α α β β α π β
则| |
,
由0< , < ,可得 ﹣ ,
α π β α β
即有cos( ﹣ ) [﹣1,0),则| |的范围为[0, ),
α β ∈
故选:A.
4.(2020•福建二模)△ABC的内角A,B,C的对边分别为a,b,c,且(2b﹣c)cosA=acosC,b=2
,若边BC的中线等于3,则△ABC的面积为( )
A.9 B. C.3 D.
【解答】解:由题意得,(2b﹣c)cosA=acosC,
根据正弦定理得,(2sinB﹣sinC)cosA=sinAcosC,
2sinBcosA=sinAcosC+cosAsinC,2sinBcosA=sin(A+C),
因为A+B+C=180°,所以①A+C=180°﹣B,则sinB=sin(A+C),
代入 得,cosA ,
①
由0°<A<180°,得,A=60°,
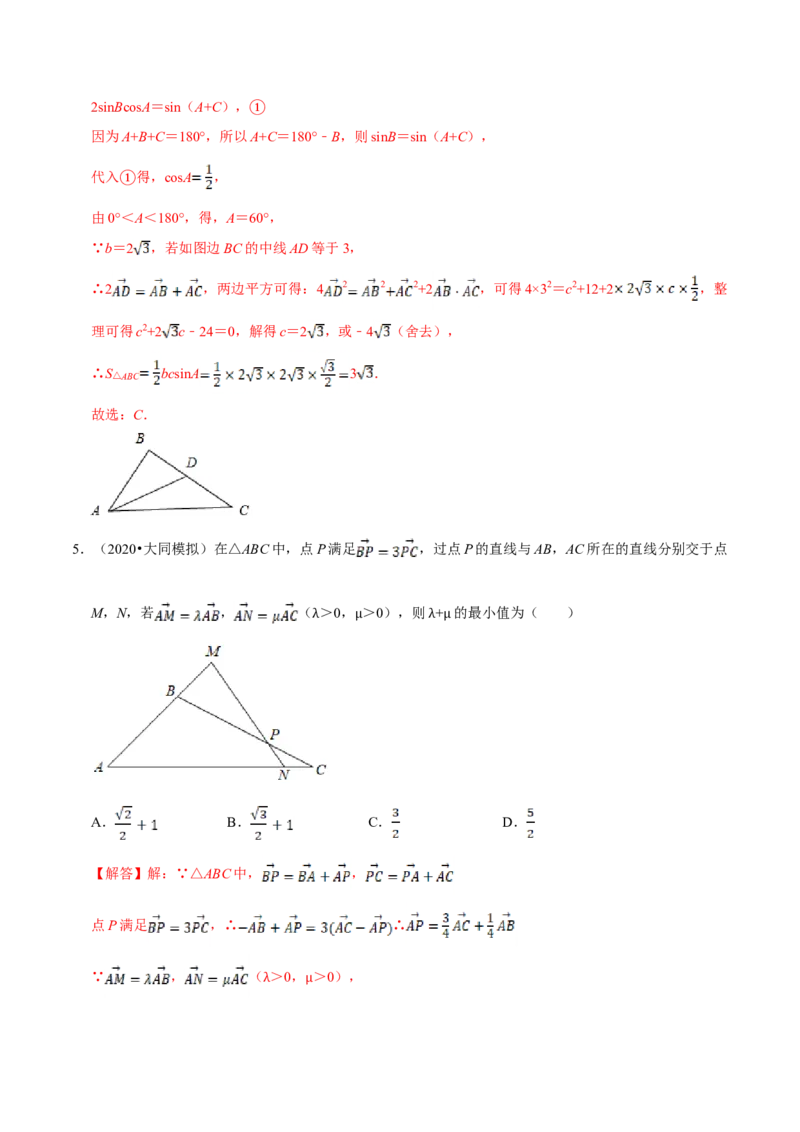
∵b=2 ,若如图边BC的中线AD等于3,
∴2 ,两边平方可得:4 2 2 2+2 ,可得4×32=c2+12+2 ,整
理可得c2+2 c﹣24=0,解得c=2 ,或﹣4 (舍去),
∴S△ABC bcsinA 3 .
故选:C.
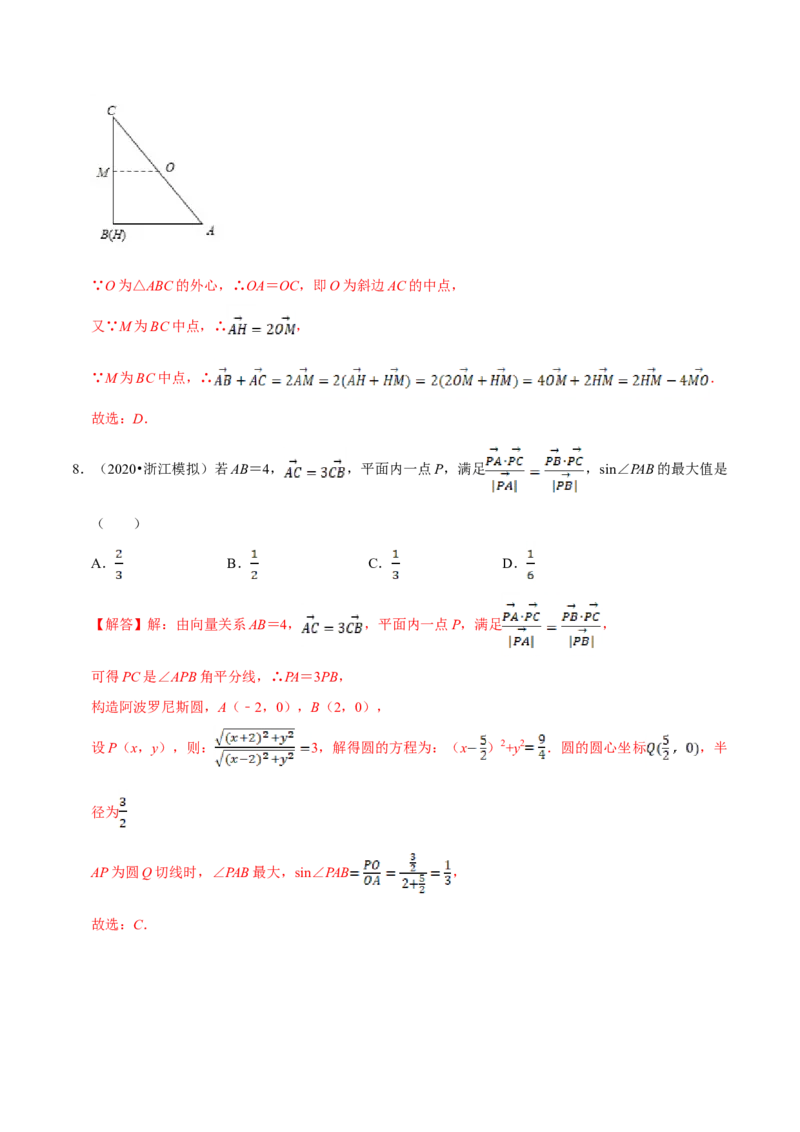
5.(2020•大同模拟)在△ABC中,点P满足 ,过点P的直线与AB,AC所在的直线分别交于点
M,N,若 , ( >0, >0),则 + 的最小值为( )
λ μ λ μ
A. B. C. D.
【解答】解:∵△ABC中, ,
点P满足 ,∴ ∴
∵ , ( >0, >0),
λ μ∴
因为B,P,C三点共线,所以, , >0, >0
λ μ
∴ + =( + )( )=1 1
λ μ λ μ
当且仅当 时取“=”,则 + 的最小值为
μ λ λ μ
故选:B.
6.(2020•麒麟区校级一模)已知数列{a }的前n项和为S ,且a =a +a(n N*,a为常数),若平面内
n n n+1 n
∈
的三个不共线的非零向量 , , 满足 ,A,B,C三点共线且该直线不过
O点,则S 等于( )
2010
A.1005 B.1006 C.2010 D.2012
【解答】解:由a =a +a得,a ﹣a =a;
n+1 n n+1 n
∴{a }为等差数列;
n
由 ,所以A,B,C三点共线;
∴a +a =a +a =1,
1005 1006 1 2010
∴S 2010=1005.
2010
故选:A.
7.(2020•深圳模拟)著名数学家欧拉提出了如下定理:三角形的外心、重心、垂心依次位于同一直线上,
且重心到外心的距离是重心到垂心距离的一半.此直线被称为三角形的欧拉线,该定理则被称为欧拉线
定理.设点O,H分别是△ABC的外心、垂心,且M为BC中点,则( )
A. B.
C. D.
【解答】解:如图所示的Rt△ABC,其中角B为直角,则垂心H与B重合,∵O为△ABC的外心,∴OA=OC,即O为斜边AC的中点,
又∵M为BC中点,∴ ,
∵M为BC中点,∴ .
故选:D.
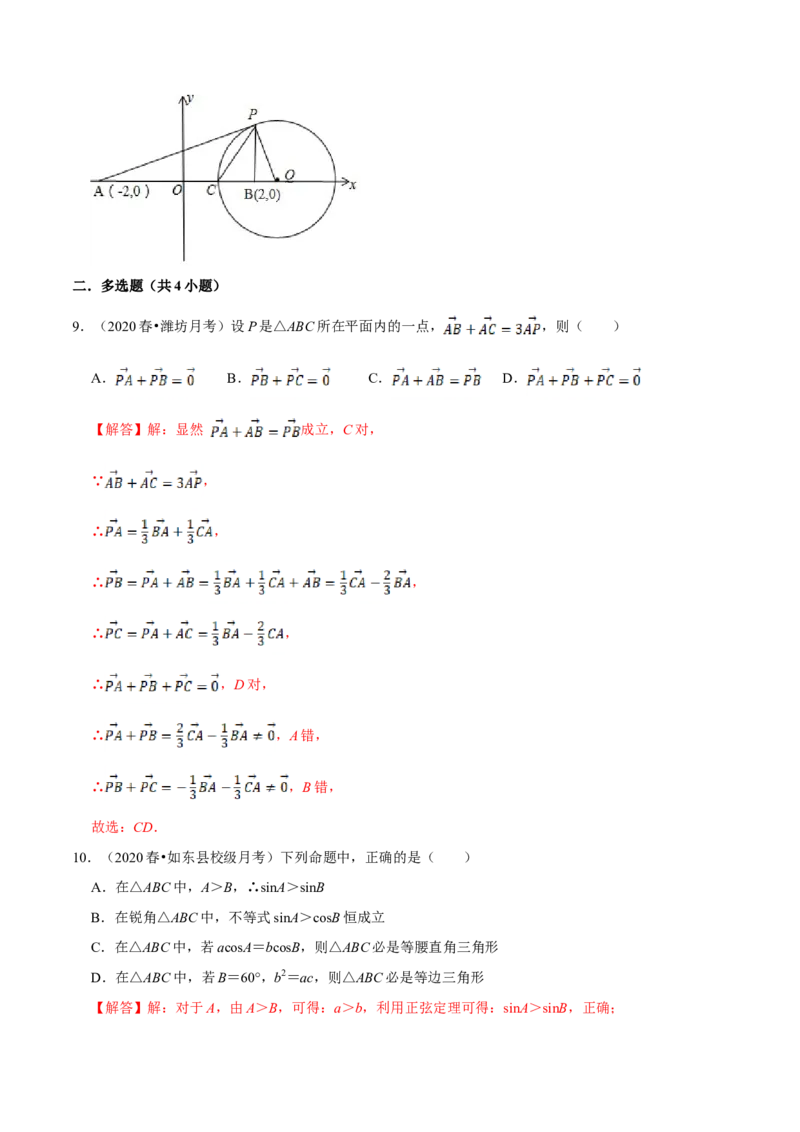
8.(2020•浙江模拟)若AB=4, ,平面内一点P,满足 ,sin∠PAB的最大值是
( )
A. B. C. D.
【解答】解:由向量关系AB=4, ,平面内一点P,满足 ,
可得PC是∠APB角平分线,∴PA=3PB,
构造阿波罗尼斯圆,A(﹣2,0),B(2,0),
设P(x,y),则: 3,解得圆的方程为:(x )2+y2 .圆的圆心坐标 ,半
径为
AP为圆Q切线时,∠PAB最大,sin∠PAB ,
故选:C.二.多选题(共4小题)
9.(2020春•潍坊月考)设P是△ABC所在平面内的一点, ,则( )
A. B. C. D.
【解答】解:显然 成立,C对,
∵ ,
∴ ,
∴ ,
∴ ,
∴ ,D对,
∴ ,A错,
∴ ,B错,
故选:CD.
10.(2020春•如东县校级月考)下列命题中,正确的是( )
A.在△ABC中,A>B,∴sinA>sinB
B.在锐角△ABC中,不等式sinA>cosB恒成立
C.在△ABC中,若acosA=bcosB,则△ABC必是等腰直角三角形
D.在△ABC中,若B=60°,b2=ac,则△ABC必是等边三角形
【解答】解:对于A,由A>B,可得:a>b,利用正弦定理可得:sinA>sinB,正确;对于B,在锐角△ABC中,A,B (0, ),∵A+B ,∴ A B>0,∴sinA>sin( B)=
∈
cosB,因此不等式sinA>cosB恒成立,正确
对于C,在△ABC中,由acosA=bcosB,利用正弦定理可得:sinAcosA=sinBcosB,
∴sin2A=sin2B,
∵A,B (0, ),
∴2A=2∈B或2Aπ=2 ﹣2B,
π
∴A=B或 ,
∴△ABC是等腰三角形或直角三角形,因此是假命题,C错误.
对于D,由于B=600,b2=ac,由余弦定理可得:b2=ac=a2+c2﹣ac,可得(a﹣c)2=0,解得a=c,
可得A=C=B=60°,故正确.
故选:ABD.
11.(2019秋•德城区校级月考)已知 , 是两个单位向量, R时,| |的最小值为 ,则下列结
λ∈ λ
论正确的是( )
A. , 的夹角是
B. , 的夹角是 或
C. |=1或
D. 1或
【解答】解:∵ , 是两个单位向量,且 的最小值为 ,
∴ 的最小值为 ,
∴ ,
∴ 与 的夹角为 或 ,
∴ 或3,
∴ 或 .
故选:BC.12.(2019春•烟台期末)在△ABC中,角A,B,C所对的边分别为a,b,c,且(a+b):(a+c):
(b+c)=9:10:11,则下
列结论正确的是( )
A.sinA:sinB:sinC=4:5:6
B.△ABC是钝角三角形
C.△ABC的最大内角是最小内角的2倍
D.若c=6,则△ABC外接圆半径为
【解答】解:(a+b):(a+c):(b+c)=9:10:11,可设a+b=9t,a+c=10t,b+c=11t,
解得a=4t,b=5t,c=6t,t>0,
可得sinA:sinB:sinC=a:b:c=4:5:6,故A正确;
由c为最大边,可得cosC 0,即C为锐角,故B错误;
由cosA ,由cos2A=2cos2A﹣1=2 1 cosC,
由2A,C (0, ),可得2A=C,故C正确;
∈ π
若c=6,可得2R ,△ABC外接圆半径为 ,故D正确.
故选:ACD.
三.填空题(共4小题)
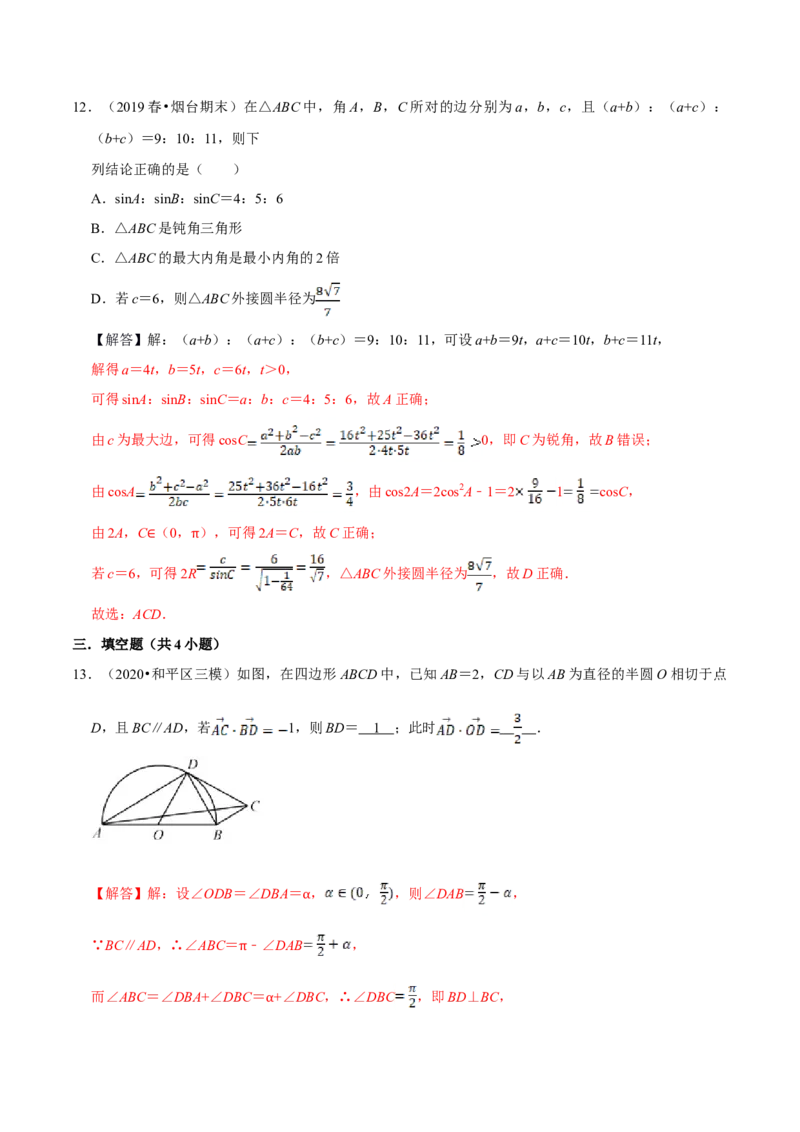
13.(2020•和平区三模)如图,在四边形ABCD中,已知AB=2,CD与以AB为直径的半圆O相切于点
D,且BC∥AD,若 1,则BD= 1 ;此时 .
【解答】解:设∠ODB=∠DBA= , ,则∠DAB ,
α
∵BC∥AD,∴∠ABC= ﹣∠DAB ,
π
而∠ABC=∠DBA+∠DBC= +∠DBC,∴∠DBC ,即BD⊥BC,
α∴ 2×(2cos )×cos( ﹣ )+0=﹣1,
α π α
∴ ,∴ ,即 ,
在Rt△ABD中,BD ,AD ,∠ADO ,
∴ .
故答案为:1; .
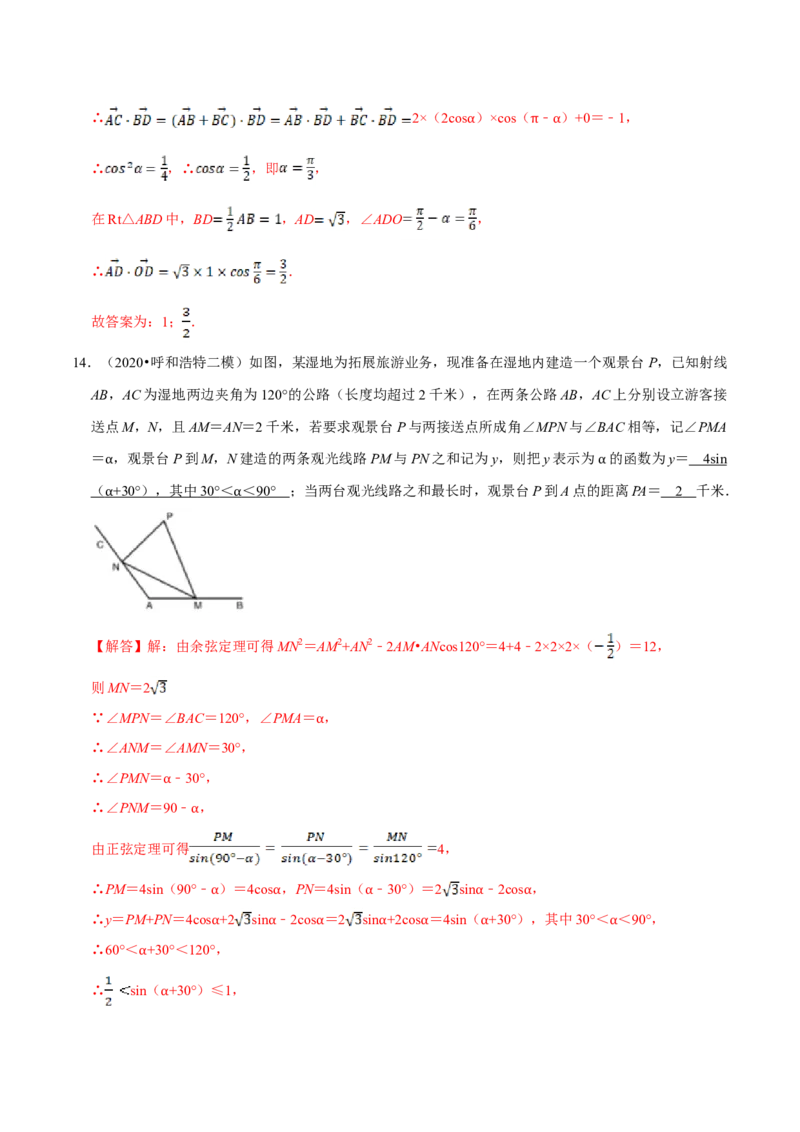
14.(2020•呼和浩特二模)如图,某湿地为拓展旅游业务,现准备在湿地内建造一个观景台 P,已知射线
AB,AC为湿地两边夹角为120°的公路(长度均超过2千米),在两条公路AB,AC上分别设立游客接
送点M,N,且AM=AN=2千米,若要求观景台P与两接送点所成角∠MPN与∠BAC相等,记∠PMA
= ,观景台P到M,N建造的两条观光线路PM与PN之和记为y,则把y表示为 的函数为y= 4si n
( α +30 ° ),其中 30 ° < < 90 ° ;当两台观光线路之和最长时,观景台P到A点的α距离PA= 2 千米.
α α
【解答】解:由余弦定理可得MN2=AM2+AN2﹣2AM•ANcos120°=4+4﹣2×2×2×( )=12,
则MN=2
∵∠MPN=∠BAC=120°,∠PMA= ,
∴∠ANM=∠AMN=30°, α
∴∠PMN= ﹣30°,
∴∠PNM=α90﹣ ,
α
由正弦定理可得 4,
∴PM=4sin(90°﹣ )=4cos ,PN=4sin( ﹣30°)=2 sin ﹣2cos ,
∴y=PM+PN=4cosα+2 sin α﹣2cos =2 sαin +2cos =4sin(α +30°)α,其中30°< <90°,
∴60°< +30°<120°α, α α α α α α
α
∴ sin( +30°)≤1,
α∴当 =60°时,此时PM+PM的长度最长,
此时αPM=PN=2,
∴PA=2,
故答案为:4sin( +30°),其中30°< <90°,2.
α α
15.(2020•浙江)设 , 为单位向量,满足|2 | , , 3 ,设 , 的夹角
为 ,则cos2 的最小值为 .
θ θ
【解答】解:设 、 的夹角为 ,由 , 为单位向量,满足|2 | ,
α
所以4 4 • 4﹣4cos +1≤2,
α
解得cos ;
α
又 , 3 ,且 , 的夹角为 ,
θ
所以 • 3 4 • 4+4cos ,
α
2 • 2+2cos ,
α
9 6 10+6cos ;
α
则cos2 ,
θ
所以cos 时,cos2 取得最小值为 .
α θ
故答案为: .
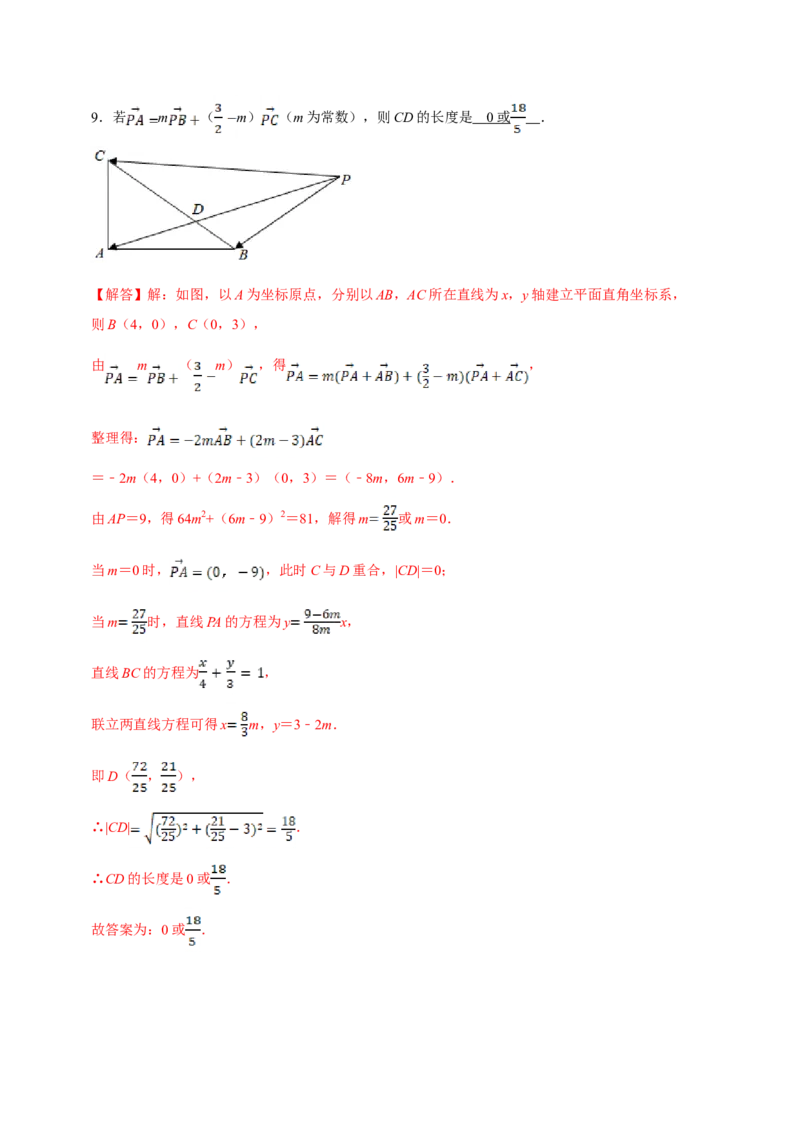
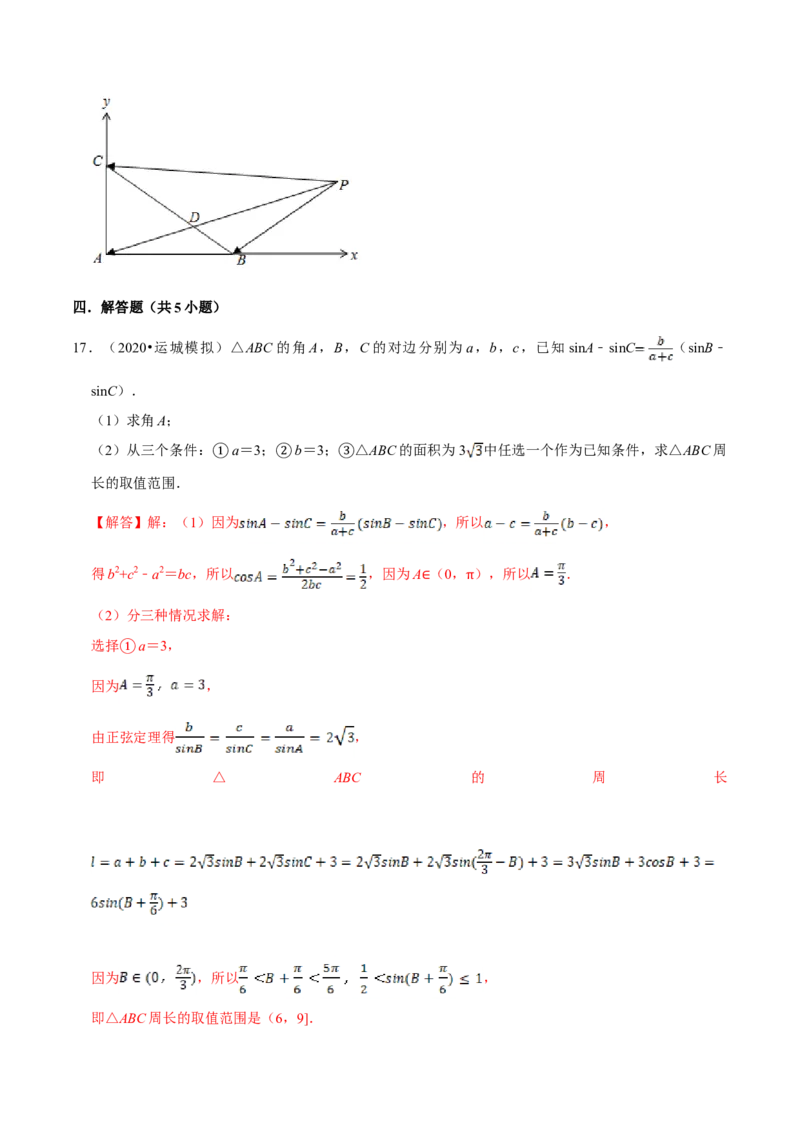
16.(2020•江苏)在△ABC中,AB=4,AC=3,∠BAC=90°,D在边BC上,延长AD到P,使得AP=9.若 m ( m) (m为常数),则CD的长度是 0 或 .
【解答】解:如图,以A为坐标原点,分别以AB,AC所在直线为x,y轴建立平面直角坐标系,
则B(4,0),C(0,3),
由 m ( m) ,得 ,
整理得:
=﹣2m(4,0)+(2m﹣3)(0,3)=(﹣8m,6m﹣9).
由AP=9,得64m2+(6m﹣9)2=81,解得m 或m=0.
当m=0时, ,此时C与D重合,|CD|=0;
当m 时,直线PA的方程为y x,
直线BC的方程为 ,
联立两直线方程可得x m,y=3﹣2m.
即D( , ),
∴|CD| .
∴CD的长度是0或 .
故答案为:0或 .四.解答题(共5小题)
17.(2020•运城模拟)△ABC的角A,B,C的对边分别为 a,b,c,已知sinA﹣sinC (sinB﹣
sinC).
(1)求角A;
(2)从三个条件: a=3; b=3; △ABC的面积为3 中任选一个作为已知条件,求△ABC周
长的取值范围. ① ② ③
【解答】解:(1)因为 ,所以 ,
得b2+c2﹣a2=bc,所以 ,因为A (0, ),所以 .
∈ π
(2)分三种情况求解:
选择 a=3,
①
因为 ,
由正弦定理得 ,
即 △ ABC 的 周 长
因为 ,所以 ,
即△ABC周长的取值范围是(6,9].选择 b=3.
②
因为 ,
由正弦定理得 ,
即△ABC的周长 ,
因为 ,所以 ,所以 ,
即△ABC周长的取值范围是(6,+∞).
选择 .
③
因为 ,得bc=12,
由余弦定理得a2=b2+c2﹣bc=(b+c)2﹣3bc=(b+c)2﹣36,
即△ABC的周长 ,
因为 ,当且仅当 时等号成立,
所以 .
即△ABC周长的取值范围是 .
18.(2020•江苏四模)在△ABC中,角A,B,C的对边分别为a,b,c.已知cosA .
(1)若△ABC的面积为3,求 的值;
(2)设 (2sin ,1), (cosB,cos ),且 ∥ ,求sin(B﹣2C)的值.
【解答】解:(1)因为cosA ,所以sinA
则S△ABC | |•| |sinA | |•| |=3,即| |•| | ,
又cosA ,所以 ;
(2)因为 ∥ ,所以2sin cos cosB,即sinB=cosB,所以B ,
因为sinA ,cosA ,sinB=cosB ,所以sinC=sin(A+B)=sinAcosB+cosAsinB ,
cosC=﹣cos(A+B)=﹣cosAcosB+sinAsinB ,
则sin2C=2sinCcosC=2 ,cos2C=2cos2﹣1=2 1 ,
所以sin(B﹣2C)=sinBcos2C﹣cosBsin2C ( ) .
19.(2020•武昌区模拟)已知△ABC中三个内角A,B,C所对的边为a,b,c,且B ,b=2.
(1)若c ,求sinA的值;
(2)当 取得最大值时,求A的值.
【解答】解:(1)在△ABC中,由正弦定理得 ,则sinC ,
因为b>c,所以C ,
则sinA=sin( ﹣B﹣C)=sin(B+C)=sinBcosC+cosBsinC ;
π
(2) bacosC=2acosC=2 cosC
sinA( A)
sinA( cosA sinA)
=2 sin(2A )
当且仅当2A ,即A 时 取到最大值.
20.(2020春•丽水期末)已知向量 (cosx+sinx, cosx), (cosx﹣sinx,﹣2sinx),记函数f
(x) • .(Ⅰ)求函数f(x)在 上的取值范围;
(Ⅱ)若g(x)=f(x+t)为偶函数,求|t|的最小值.
【解答】解:(Ⅰ)f(x) (cosx+sinx)(cosx﹣sinx)﹣2 sinxcosx
=cos2x﹣sin2x sin2x
=cos2x sin2x=2cos(2x ),
因为x [0, ],则 ,所以﹣1≤cos(2x ) ,
∈
则f(x)的取值范围为[﹣2,1];
(Ⅱ)若g(x)=f(x+t)=2cos(2x+2t )为偶函数,
则2t k (k Z),即t (k Z),
π ∈ ∈
故|t|的最小值为 .
21.(2020•泰安模拟)在 asinC C; 5ccosB+4b=5a; (2b﹣a)cosC=
ccosA,这三个条件中任①选一个,补充在下面问题中,然后解答补②充完整的题目. ③
在△ABC中,内角A,B,C所对的边分别为a,b,c.且满足______.
(1)求sinC;
(2)已知a+b=5,△ABC的外接圆半径为 ,求△ABC的边AB上的高h.
【解答】解:选择条件 :
(1)因为 ① ,
所以由正弦定理得 ,
即 ,
故 ,
又A (0, ),故sinA≠0,
所以∈ π .
由 .
所以 ,(2)由正弦定理得 ,
由余弦定理得 ,
所以 ,
于是得△ABC的面积 ,
所以 ,
选择条件 :
(1)因为②5ccosB+4b=5a,
由正弦定理得5sinCcosB+4sinB=5sinA,
即5sinCcosB+4sinB=5sin(B+C)=5sinBcosC+5cosBsinC,
于是sinB(4﹣5cosC)=0,
在△ABC中,sinB≠0,
所以 , ,
(2)由正弦定理得 ,
由余弦定理得c2=a2+b2﹣2abcosC ,
所以 ,
于是得△ABC的面积 ,
所以 ,
选择条件 :
(1)因为③(2b﹣a)cosC=ccosA,
所以由正弦定理得(2sinB﹣sinA)cosC=sinCcosA,
所以2sinBcosC=sin(A+C)=sinB,
因为B (0, ),
∈ π
所以 ,又C (0, ),
∈ π
所以 ,
所以 .
(2)由正弦定理得 ,
由余弦定理得 ,
所以 ,
于是得△ABC的面积 ,
所以 .