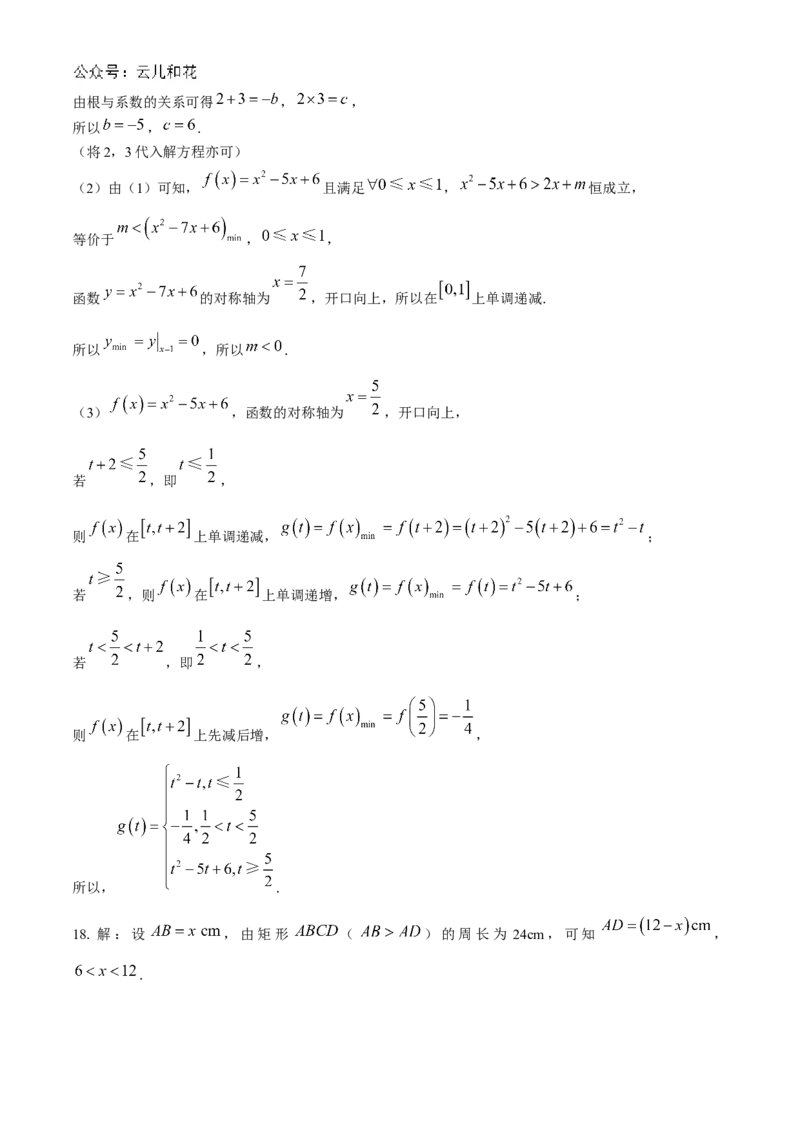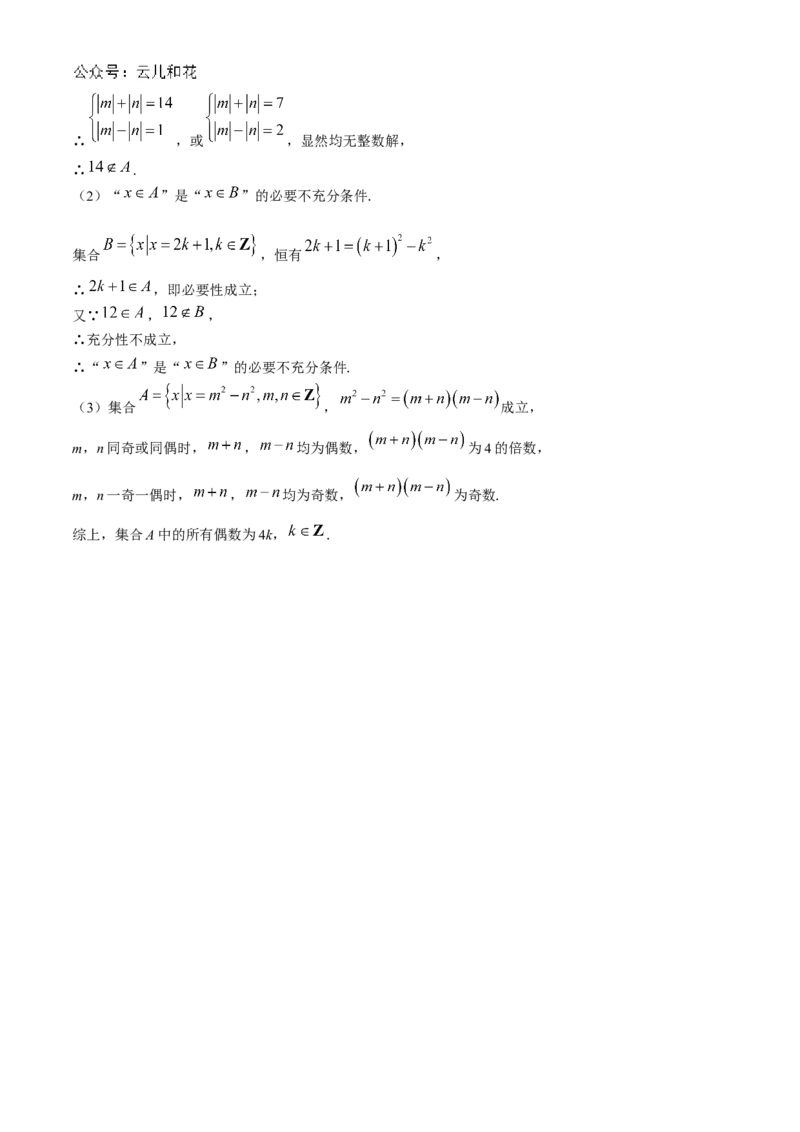文档内容
六校联盟 2024 年 11 月期中联考
高一数学试题
考生注意:
1.本试卷分选择题和非选择题两部分。满分150分,考试时间120分钟。
2.答题前,考生务必用直径0.5毫米黑色墨水签字笔将密封线内项目填写清楚。
3.考生作答时,请将答案答在答题卡上。选择题每小题选出答案后,用2B铅笔把答题卡上对
应题目的答案标号涂黑;非选择题请用直径 0.5毫米黑色墨水签字笔在答题卡上各题的答题
区域内作答,超出答题区域书写的答案无效,在试题卷、草稿纸上作答无效。
4.本卷命题范围:人教A版必修第一册第一章~第三章。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项
是符合题目要求的。
1.已知全集 , , ,则 ( )
A. B. C. D.
2.不等式 的解集是( )
A. B. C. D.
3.函数 的定义域是( )
A. B. C. D.
4.某班同学参加课外兴趣小组,有三个兴趣小组可供选择,要求每位同学至少选择一个小组,经统计有20
人参加奥数小组,16人参加编程小组,10人参加书法小组,同时参加奥数小组和编程小组的有12人,同
时参加奥数小组和书法小组的有6人,同时参加编程小组和书法小组的有5人,三种都参加的有3人,则
该班学生人数为( )
A.27 B.23 C.26 D.29
5.“ ”是“ ”的( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
6.已知 , ,下列对应关系不能作为从集合A到集合B的函数的是( )A.f: B.f: C.f: D.f:
7.命题“ , ”的否定为假命题,则k的取值范围是( )
A. B. C. D.
8.已知 是定义域为 的偶函数,且当 时, 是增函数.若 ,则m
的取值范围为( )
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题
目要求。全部选对的得6分,部分选对的得部分分,有选错的得0分。
9.下列命题为假命题的是( )
A.若 ,则 B.若 ,则
C.若 ,则 D.若 ,则
10.下列各项中, 与 表示同一函数的是( )
A. , B. ,
C. , D. ,
11.已知关于x的不等式 ( , )的解集为 ,
则下列结论正确的是( )
A. B. 的最大值为
C. 的最小值为 D. 的最小值为
三、填空题:本题共3小题,每小题5分,共15分。12.已知 ,则 .
13.已知定义域为 的奇函数 ,则 的值为 .
14.已知集合 ,则M的真子集的个数是 .
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15.(本小题满分13分)
若集合 , .
(1)若 ,求 ;
(2)当 时,求实数m的取值范围.
16.(本小题满分15分)
已知函数 ,且 , .
(1)求a和b的值;
(2)判断 在 上的单调性,并根据定义证明.
17.(本小题满分15分)
已知函数 与x轴的两个交点为 , .
(1)求b,c的值;
(2)在 上,函数 的图象总在一次函数 的图象的上方,求实数m的取值范围;
(3)设当 ( )时,函数 的最小值为 ,求 的解析式.
18.(本小题满分17分)
设矩形 ( )的周长为24cm,把 沿 向 折叠, 折过去后交 于点
P.求 的最大面积和此时 的长.
19.(本小题满分17分)
已知集合 .
(1)判断5,12,14,21是否属于A;(2)集合 ,判断“ ”是“ ”的什么条件(充要条件,充分不必要条
件,必要不充分条件,既不充分也不必要条件),并说明理由;
(3)写出集合A中的所有偶数.六校联盟 2024 年 11 月期中联考·高一数学
参考答案、提示及评分细则
1.A 2.D 3.D 4.C 5.B 6.A 7.C 8.B 9.ACD 10.BCD 11.AB
12.2 13.0 14.31
15.解:
(1)∵ ,∴ ,
∴ .
(2)∵ ,∴ ,
∴ ,
∴ .
16.解:
(1)∵ , ,∴ , .
∴ , .
(2)由(1)得 , 在 上单调递减,证明如下:
, , ,
.
∵ ,∴ ,
∴ ,
在 上单调递减.
17.解:
(1)2,3为方程 的两根,由根与系数的关系可得 , ,
所以 , .
(将2,3代入解方程亦可)
(2)由(1)可知, 且满足 , 恒成立,
等价于 , ,
函数 的对称轴为 ,开口向上,所以在 上单调递减.
所以 ,所以 .
(3) ,函数的对称轴为 ,开口向上,
若 ,即 ,
则 在 上单调递减, ;
若 ,则 在 上单调递增, ;
若 ,即 ,
则 在 上先减后增, ,
所以, .
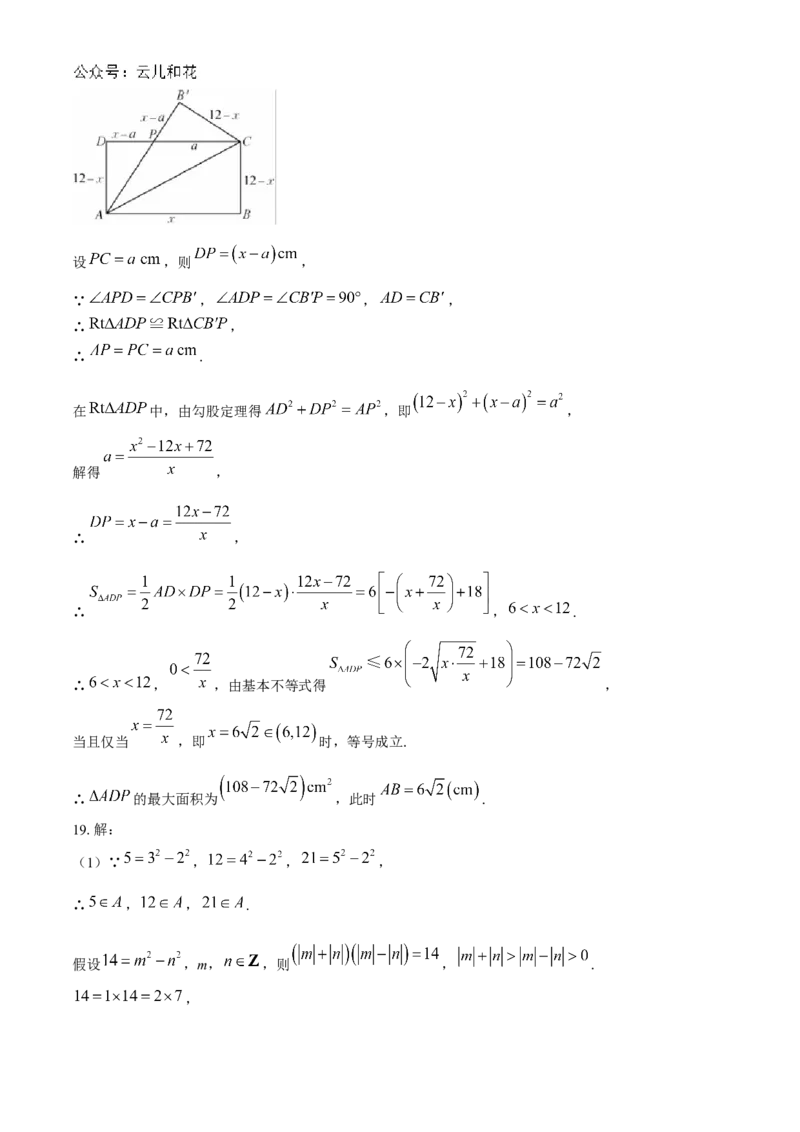
18.解:设 ,由矩形 ( )的周长为 24cm,可知 ,
.设 ,则 ,
∵ , , ,
∴ ,
∴ .
在 中,由勾股定理得 ,即 ,
解得 ,
∴ ,
∴ , .
∴ , ,由基本不等式得 ,
当且仅当 ,即 时,等号成立.
∴ 的最大面积为 ,此时 .
19.解:
(1)∵ , , ,
∴ , , .
假设 ,m, ,则 , .
,∴ ,或 ,显然均无整数解,
∴ .
(2)“ ”是“ ”的必要不充分条件.
集合 ,恒有 ,
∴ ,即必要性成立;
又∵ , ,
∴充分性不成立,
∴“ ”是“ ”的必要不充分条件.
(3)集合 , 成立,
m,n同奇或同偶时, , 均为偶数, 为4的倍数,
m,n一奇一偶时, , 均为奇数, 为奇数.
综上,集合A中的所有偶数为4k, .