文档内容
高二下数学半期考试试题(高考班)
一、单选题(本题共8小题,每小题5分,共40分)
1. 下列导数运算正确的是( )
A. B.
C. D.
【答案】B
【解析】
【分析】利用基本初等函数的导数和复合函数的导数,依次分析即得解
【详解】选项A, ,错误;
选项B, ,正确;
选项C, ,错误;
选项D, ,错误
故选:B
2. 曲线 在 处的切线方程为( )
A. B. C. D.
【答案】A
【解析】
【分析】求出导函数 ,计算出 为切线斜率,再求得 ,由点斜式写出直线方程,并整理.
【详解】 , , ,故切线方程为 ,即 .
故选:A.
学科网(北京)股份有限公司3. 从 中任取 个不同的数,事件 “取到的 个数之和为偶数”,事件 “取到两个数均
为偶数”,则
A. B. C. D.
【答案】B
【解析】
【分析】先求得 和 的值,然后利用条件概率计算公式,计算出所求的概率.
【详解】依题意 , ,故 .故选B.
【点睛】本小题主要考查条件概型的计算,考查运算求解能力,属于基础题.
4. 已知某批零件的长度误差(单位:毫米)服从正态分布 ,从中随机取一件,其长度误差落在
区间(3,6)内的概率为
(附:若随机变量ξ服从正态分布 ,则 ,
.)
A. 4.56% B. 13.59% C. 27.18% D. 31.74%
【答案】B
【解析】
【 详 解 】 试 题 分 析 : 由 题 意
故选B.
考点:正态分布
5. 2020年12月1日,大连市开始实行生活垃圾分类管理.某单位有四个垃圾桶,分别是一个可回收物垃圾
桶、一个有害垃圾桶、一个厨余垃圾桶、一个其它垃圾桶.因为场地限制,要将这四个垃圾桶摆放在三个固定
学科网(北京)股份有限公司角落,每个角落至少摆放一个,则不同的摆放方法共有(如果某两个垃圾桶摆放在同一角落,它们的前后左
右位置关系不作考虑)( )
A. 种 B. 种 C. 种 D. 种
【答案】C
【解析】
【分析】
分析题意,得到有一个固定点放着两个垃圾桶,先选出两个垃圾桶,之后相当于三个元素分配到三个地方,
最后利用分步乘法计数原理,求得结果.
【详解】根据题意,有四个垃圾桶放到三个固定角落,其中有一个角落放两个垃圾桶,
先选出两个垃圾桶,有 种选法,
之后与另两个垃圾桶分别放在三个不同的地方有 种放法;
所以不同的摆放方法共有 种,
故选:C.
【点睛】思路点睛:该题考查的是有关排列组合综合题,解题方法如下:
(1)首先根据题意,分析出有两个垃圾桶分到同一个地方,有 种选法;
(2)之后就相当于三个元素的一个全排;
(3)利用分步乘法计数原理求得结果.
6. 已知变量 , 之间的线性回归方程为 ,且变量 , 之间的一组相关数据如表所示,
则下列说法错误的是( )
6 8 10 12
6 3 2
A. 变量 , 之间呈负相关关系 B.
C. 可以预测,当 时, D. 该回归直线必过点
【答案】B
【解析】
【分析】
学科网(北京)股份有限公司A.由回归方程 的x的系数判断;B.将 。代入回归方程求得 即可;C. 将 代
入回归直线方程判断; D.根据回归直线过点 判断.
【详解】A.由回归方程 知 ,所以变量 , 之间呈负相关关系,故正确;
B.因为 。则 ,所以 ,
解得 ,故错误;
C. 当 时, ,故正确;
D.由B知: , ,所以回归直线必过点 ,故正确;
故选:B
7. ( + )(2 - )5的展开式中 3 3的系数为
A. -80 B. -40 C. 40 D. 80
【答案】C
【解析】
【详解】 ,
由 展开式的通项公式 可得:
当 时, 展开式中 的系数为 ;
当 时, 展开式中 的系数为 ,
则 的系数为 .
故选C.
【名师点睛】(1)二项式定理的核心是通项公式,求解此类问题可以分两步完成:第一步根据所给出
的条件(特定项)和通项公式,建立方程来确定指数(求解时要注意二项式系数中n和r的隐含条件,即
n,r均为非负整数,且n≥r,如常数项指数为零、有理项指数为整数等);第二步是根据所求的指数,
再求所求解的项.
(2)求两个多项式的积的特定项,可先化简或利用分类加法计数原理讨论求解.
学科网(北京)股份有限公司8. 若函数 在区间 上单调递增,则实数 的取值范围是
A. B. C. D.
【答案】D
【解析】
【详解】试题分析: ,∵函数 在区间 单调递增,∴ 在区间
上恒成立.∴ ,而 在区间 上单调递减,∴ .∴ 的取值范围是 .故
选D.
考点:利用导数研究函数的单调性.
二、多选题(共4小题,每小题5分,共20分,全部选对得5分,部分选对得2分,有选错的
得0分)
9. 关于变量x,y的n个样本点 及其线性回归方程. 下列说法正确
的有( )
A. 相关系数r的绝对值|r|越接近0,表示x,y的线性相关程度越强
B. 相关指数 的值越接近1,表示线性回归方程拟合效果越好
C. 残差平方和越大,表示线性回归方程拟合效果越好
D. 若 ,则点 一定在线性回归方程 上
【答案】BD
【解析】
【分析】
根据回归分析的相关知识,逐一分析四个选项的正误即可.相关系数的绝对值越接近0,线性相关度越弱.相
关指数表示拟合效果的好坏,指数越大,拟合程度越好.残差平方和越小,拟合程度越好.线性回归方程一
定过样本中心点.
【详解】根据线性相关系数的意义可知,当 的绝对值越接近于0时,
两个随机变量线性相关性越弱,则A错误;
学科网(北京)股份有限公司用相关指数 来刻画回归效果,
越大,说明模型的拟合效果越好,则B正确;
拟合效果的好坏是由残差平方和来体现的,
残差平方和越大,拟合效果越差,则C错误;
样本中心点一定在回归直线上,则D正确.
故选:BD.
10. 设离散型随机变量 的分布列如下表:
1 2 3 4 5
0.1 0.2 0.3
若离散型随机变量 ,且 ,则( )
.
A B. C. D.
【答案】BC
【解析】
【分析】先由 可得 ,再由概率和为1得 ,从而可求出 的值,再利
用期望和方差公式求 , 即可,从而可得答案
【详解】由 得 ,又由
得 ,从而得 , ,故A选项错误,B选项正确;
,故C选项正确;
因为 ,所以
,故D选项错误,
故选:BC.
11. 一个口袋中有大小形状完全相同的3个红球和4个白球,从中取出2个球.下面几个命题中正确的是(
)
学科网(北京)股份有限公司A. 如果是不放回地抽取,那么取出两个红球和取出两个白球是对立事件
B. 如果是不放回地抽取,那么第2次取到红球的概率一定小于第1次取到红球的概率
C. 如果是有放回地抽取,那么取出1个红球1个白球的概率是
D. 如果是有放回地抽取,那么在至少取出一个红球的条件下,第2次取出红球的概率是
【答案】CD
【解析】
【分析】对于A,利用对立事件的概念判断即可;对于B,分别计算出第2次取到红球的概率和第1次取
得红球的概率进行比较即可;对于C,有放回地抽取,取出1个红球1个白球包括第1次为红球第2次为白
球、第1次为白球第2次为红球,然后求出概率;对于D,有放回地抽取,至少取出一个红球的条件下,
第2次取出红球包括第1 次红球第2次白球、第1次白球第2次红球、两次都是红球,从而可求得其概率
【详解】对于A,不放回地抽取两个球,包括两个都是红球、两个都是白球和一个红球一个白球,共3种
情况,所以取出两个红球和取出两个白球不是对立事件,所以A错误;
对于B,不放回地抽取,第2次取到红球 的概率为 ,第1次取得红球的概率为 ,所以
第2次取到红球的概率等于第1次取到红球的概率,所以B错误;
对于C,有放回地抽取,取出1个红球1个白球包括第1次为红球第2次为白球、第1次为白球第2次为红
球,所以所求概率为 ,所以C正确,
对于D,有放回地抽取,至少取出一个红球的条件下,第2次取出红球包括第1 次红球第2次白球、第1
次白球第2次红球、两次都是红球,所以所求概率为 ,所以D正确,
故选:CD
12. 已知函数 在 上可导且 ,其导函数 满足 ,对于函
学科网(北京)股份有限公司数 ,下列结论正确的是( )
A. 函数 在 上为增函数 B. 是函数 的极小值点
C. 函数 必有2个零点 D.
【答案】BD
【解析】
【分析】
对函数 求导,求出单调区间和极值,可判断选项A,B;根据极小值的大小可得函数的零点个数,判
断选项C;利用 在 上为增函数,比较 与 的大小关系,判断出选项D.
【详解】函数 ,则 ,
当 时, ,故 在 上为增函数,A错误;
当 时, ,故 在 单调递减,故 是函数g(x)的极小值点,B正
确;
若 ,则 有两个零点,
若 ,则 有一个零点,
若 ,则 没有零点,故C错误;
在 上为增函数,则 ,即 ,化简得 ,D正确;
故选:BD
【点睛】本题考查导数在单调性中的应用,考查函数的极值,考查函数的零点问题,考查利用单调性比较
大小,属于中档题.
三、填空题(每小题5分,共20分,其中16题第一个空2分,第二个空3分)
13. 某学校派出4名学生和2名老师参加一个活动,活动结束后他们准备站成一排拍照留念,则2名老师
相邻的不同排法有___________种.(用数字作答)
学科网(北京)股份有限公司【答案】240
【解析】
【分析】利用捆绑法即得.
【详解】因为2名老师相邻,把他们捆绑看作一个元素与4名学生排共有 种排法,再排其内部顺序又
种,
所以4名学生和2名老师站成一排拍照,2名老师相邻的不同排法有 种.
故答案为:240.
14. 对正在横行全球的“新冠病毒”,某科研团队研发了一款新药用于治疗,为检验药效,该团队从“新冠”
感染者中随机抽取100名,检测发现其中感染了“普通型毒株”,“德尔塔型毒株”、“其他型毒株”的人数占
比为 .对他们进行治疗后,统计出该药对“普通型毒株”、“德尔塔型毒株”、“其他型毒株”的有效率
分别为82%、60%、75%,那么你预估这款新药对 “新冠病毒”的总体有效率是________.
【答案】74%
【解析】
【分析】根据题意,结合概率的计算公式,准确计算,即可求解.
【详解】由题意,感染了“普通型毒株”,“德尔塔型毒株”、“其他型毒株”的人数占比为 且该药对“普
通型毒株”、“德尔塔型毒株”、“其他型毒株”的有效率分别为82%、60%、75%,
所以这款新药对 “新冠病毒”的总体有效率为 .
故答案为: .
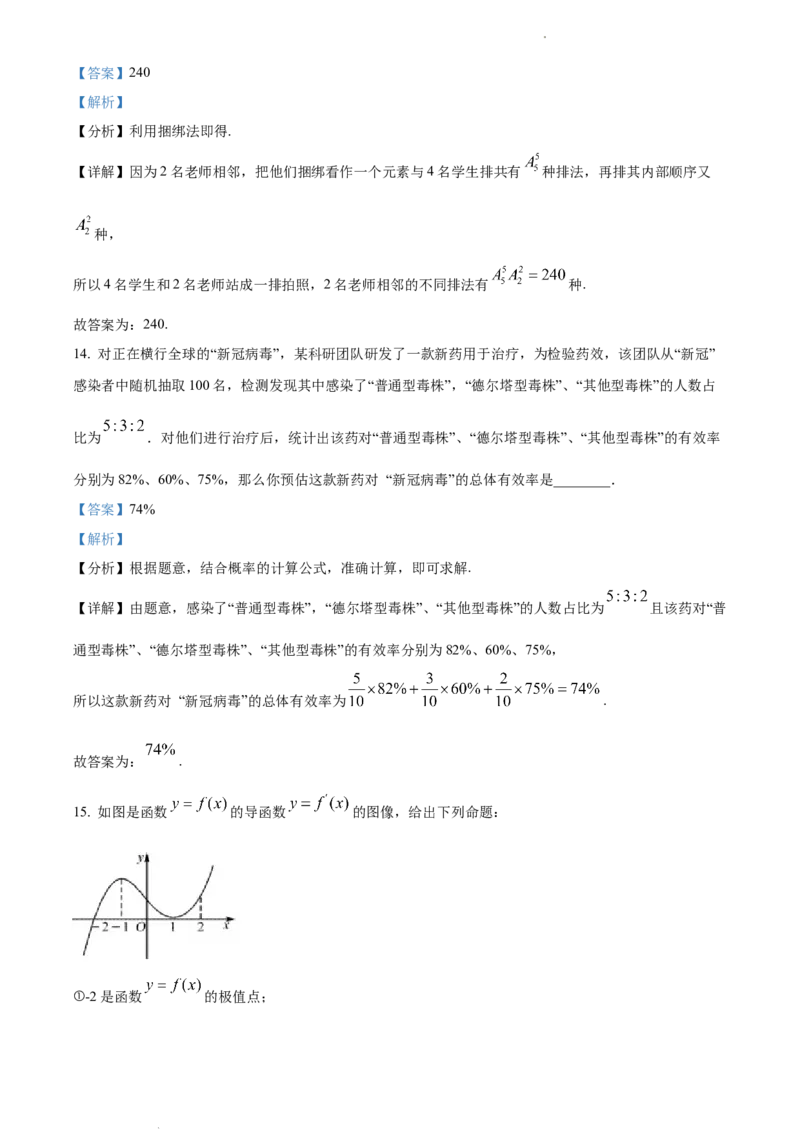
15. 如图是函数 的导函数 的图像,给出下列命题:
①-2是函数 的极值点;
学科网(北京)股份有限公司在
②函数 处取最小值;
③函数 在 处切线的斜率小于零;
④函数 在区间 上单调递增.
则正确命题的序号是__________.
【答案】①④
【解析】
【分析】根据导函数函数值的正负,即可求得 的单调性和极值点.
【详解】根据导函数 的图象可得,
当 上, ,在 上, ,
故函数在 上函数 单调递减,
在 和 ,函数 单调递增,
所以 是函数 的极小值点,所以①正确;
函数在 上单调递增,在 处取不到函数 的最小值,所以②不正确;
由 图象可得 ,
所以函数 在 处的切线的斜率大于零,所以③不正确;
由 图象可得,当 时, ,
所以函数 在 上单调递增,所以④是正确的,
综上可知,①④是正确的.
故答案为:①④.
【点睛】本题考查导函数的图象与原函数的关系,属基础题.
16. 设 .若 ,则
学科网(北京)股份有限公司实数 ________, ________.
【答案】 ①. ##0.5 ②.
【解析】
【分析】令 ,即可求出 的值.再分别求出 与 展开式中的 的系数,再求和即为 的
值.
【详解】令 ,则
解得: .
的第 项系数为 .
所以 展开式中的 的系数为 ;
的第 项系数为 .
所以 展开式中的 的系数为 ;
故答案为: ; .
【点睛】本题考查二项式定理.属于基础题.
四、解答题(17题10分,其余题12分每道 共70分)
17. 已知函数 在 处取得极值.
(1)求实数 的值;
(2)当 时,求函数 的最小值.
【答案】(1) ;(2) .
【解析】
【分析】(1)求导,根据极值的定义可以求出实数 的值;
学科网(北京)股份有限公司(2)求导,求出 时的极值,比较极值和 之间的大小的关系,最后求出函数的最小
值.
【详解】(1) ,函数 在 处取得极值,
所以有 ;
(2)由(1)可知: ,
当 时, ,函数 单调递增,当 时, ,函数 单调递减,
故函数在 处取得极大值,因此 ,
, ,故函数 的最小值为 .
【点睛】本题考查了求闭区间上函数的最小值,考查了极值的定义,考查了数学运算能力.
18. 已知 在的展开式中,第6项为常数项.
(1)求 ;
(2)求含 的项的系数;
(3)求展开式中所有的有理项.
【答案】(1) ;(2) ;(3) , , .
【解析】
【分析】
(1)求出 的展开式的通项为 ,当 时,指数为零,可得 ;
(2)将 代入通项公式,令指数为 ,可得含 的项的系数;
学科网(北京)股份有限公司(3)根据通项公式与题意得 ,求出 的值,代入通项公式并化简,可得展开式中所有的有
理项.
【详解】(1) 的展开式的通项为 ,因为第6
项为常数项,所以 时,有 ,解得 .
(2)令 ,得 ,所以含 的项的系数为 .
(3)根据通项公式与题意得 ,令 ,则 ,即 .
,∴ 应为偶数.又 ,∴ 可取2,0,-2,即 可取2,5,8.所以第3项,第6项与第9
项为有理项,它们分别为 , , ,即 , , .
【点睛】关键点点睛:本题考查二项式展开式的应用,考查二项式展开式的通项公式以及某些特定的项,
解决本题的关键点是求解展开式的有理项时,令 ,由 以及 ,求出 的
值,进而得出 的值,代入通项公式化简可得有理项,考查了学生计算能力,属于中档题.
19. 甲、乙两机床加工同一种零件,抽检得到它们加工后的零件尺寸x(单位:cm)及个数y,如下表:
零件尺寸x 1.01 1.02 1.03 1.04 1.05
零件个数y 甲 3 7 8 9 3
学科网(北京)股份有限公司乙 7 4 4 4 a
由表中数据得y关于x的经验回归方程为 ,其中合格零件尺寸为
.
(1)求a的值
(2)完成 列联表,并依据小概率值 的独立性检验,分析加工零件的质量与甲、乙机床是否
有关.
附: ,
α
【答案】(1) ;
(2)列联表见解析,认为加工零件的质量与甲、乙机床有关.
【解析】
【分析】(1)根据给定数表,求出样本的中心点,再根据经验回归方程必过样本中心点,列式计算作答.
(2)完善 列联表,计算 的观测值,再与临界值比对即可作答.
【小问1详解】
依题意, , ,
由 ,得 ,解得 ,
所以a的值为11.
【小问2详解】
由于合格零件尺寸为 ,
所以甲、乙机床加工的合格与不合格零件的 列联表为:
零件的质量
机床加工 合计
合格零件数 不合格零件数
学科网(北京)股份有限公司甲 24 6 30
乙 12 18 30
合计 36 24 60
令零假设为 :加工零件的质量与甲、乙机床无关,
则 ,
因此根据小概率值 的独立性检验,推断 不成立,
所以认为加工零件的质量与甲、乙机床有关.
20. 甲、乙去某公司应聘面试.该公司的面试方案为:应聘者从6道备选题中一次性随机抽取3道题,按照
答对题目的个数为标准进行筛选.已知6道备选题中应聘者甲有4道题能正确完成,2道题不能完成;应聘
者乙每题正确完成的概率都是 ,且每题正确完成与否互不影响.
(1)分别求甲、乙两人正确完成面试题数的分布列,并计算其数学期望;
(2)请分析比较甲、乙两人谁的面试通过的可能性较大?
【答案】(1) 甲、乙的分布列见解析;甲的数学期望2、乙的数学期望2; (2)甲通过面试的概率较大.
【解析】
【分析】(1)设出甲、乙正确完成面试题的数量分别为 , ,由于 , ,
分别写出分布列,再求期望值均为 ;
的
(2)由于均值相等,可通过比较各自 方差.
【详解】(1)设 为甲正确完成面试题的数量, 为乙正确完成面试题的数量,
依题意可得: ,
∴ , , ,
∴X的分布列为:
X 1 2 3
P
学科网(北京)股份有限公司∴ .
,
∴ , ,
, ,
∴Y的分布列为:
Y 0 1 2 3
P
∴ .
(2) ,
,
∵ ,
∴甲发挥的稳定性更强,则甲通过面试的概率较大.
【点睛】本题考查超几何分布和二项分布的应用、期望和方差的计算,考查数据处理能力,求解时注意概
率计算的准确性.
21. 今年中国共产党迎来了建党100周年,为了铭记建党历史、缅怀革命先烈、增强爱国主义情怀,某区
组织了党史知识竞赛活动.在最后一轮晋级比赛中,甲、乙、丙三所学校回答一道有关红色革命根据地建立
时间的问题,已知甲校回答正确这道题的概率为 ,甲、丙两所学校都回答正确这道题的概率是 ,乙、
学科网(北京)股份有限公司丙两所学校都回答正确这道题的概率是 .若各学校回答这道题是否正确是互不影响的.
(1)若规定三个学校都需要回答这个问题,求甲、乙、丙三所学校中至少1所学校回答正确这道题的概率;
(2)若规定三所学校需要抢答这道题,已知甲校抢到答题机会的概率为 ,乙校抢到的概率为 ,丙校
抢到的概率为 ,求这个问题回答正确的概率.
【答案】(1)
(2)
【解析】
【分析】(1)设甲、乙、丙3校答对这道题的概率分别为 , , ,利用独立事件的概率
公式结合题干条件列出方程,求解 , ,再利用对立事件的概率公式,即得解;
(2)利用全概率公式结合题干条件,即得解
【
小问1详解】
记甲、乙、丙3校独自答对这道题分别为事件 , , ,分别设甲、乙、丙3校答对这道题的概率分别
为 , , ,由于每人回答问题正确与否是相互独立的,因此 , , 是相互独立事件
由题意可知 , , ,
解得 , .
所以,乙答对这道题的概率为 ,丙答对这道题的概率为 .
甲、乙、丙三所学校中至少1所学校回答正确为事件 ,则概率为 ,其反面是三所学校都回答错误,
学科网(北京)股份有限公司即
则三所学校中至少1所学校回答正确的概率为 ;
【小问2详解】
若规定三所学校需要抢答这道题,
则这个问题回答正确设为事件 ,得到抢答机会分别是事件 , , ,则
, , , , , ,
则
这个问题回答正确的概率为 .
22. 已知函数 , .
(1)讨论 的单调性;
(2)若对任意 ,都有 成立,求实数 的取值范围.
【答案】(1)当 时,在 上, 是减函数,当 时,在 上, 是减函数,在
上, 是增函数;(2)
【解析】
【分析】求出函数的定义域,函数的导数,通过a的范围讨论,判断函数的单调性即可.(2)
对任意x>0,都有f(x)>0成立,转化为在(0,+∞)上f(x) >0,利用函数的导数求解函数的最值
min
即可.
【详解】(1)解:函数f(x)的定义域为(0,+∞)
学科网(北京)股份有限公司又
当a≤0时,在(0,+∞)上,f′(x)<0,f(x)是减函数
当a>0时,由f′(x)=0得: 或 (舍)
所以:在 上,f′(x)<0,f(x)是减函数
在 上,f′(x)>0,f(x)是增函数
(2)对任意x>0,都有f(x)>0成立,即:在(0,+∞)上f(x) >0
min
由(1)知:当a≤0时,在(0,+∞)上f(x)是减函数,
又f(1)=2a﹣2<0,不合题意
当a>0时,当 时,f(x)取得极小值也是最小值,
所以:
令 (a>0)
所以:
在(0,+∞)上,u′(a)>0,u(a)是增函数又u(1)=0
所以:要使得f(x) ≥0,即u(a)≥0,即a≥1,
min
故:a的取值范围为[1,+∞)
【点睛】本题考查函数的导数的应用,函数的最值的求法,考查转化思想以及计算能力.
学科网(北京)股份有限公司