文档内容
2024 青岛三模数学试题
一、选择题: 本题共 8 小题, 每小题 5 分, 共 40 分. 在每小题给出的四个选项中, 只有一项是符
合题 目要求的.
z-1
1. 已知复数 z 满足 =i ,则 ´z 的虚部为( )
1-i
A. -i B. i C. -1 D. 1
( π)
2. 已知命题 p:∀x∈ 0, ,sinxx B. ∃x∈ 0, ,sinx>x
2 2
( π) ( π)
C. ∃x∉ 0, ,sinx≥x D. ∃x∈ 0, ,sinx≥x
2 2
3. 为了得到 y=sin2x+cos2x 的图象,只要把 y=❑√2cos2x 的图象上所有的点( )
π π
A. 向右平行移动 个单位长度 B. 向左平行移动 个单位长度
8 8
π π
C. 向右平行移动 个单位长度 D. 向左平行移动 个单位长度
4 4
4. 某校高一有学生 980 人,在一次模拟考试中这些学生的数学成绩 X 服从正态分布 N(100,σ2)
,已知 P(90b>0) 的左,右焦点分别为 F ,F ,左、右顶点分 别
a2 b2 1 2
为 A,B ,焦距为 2c ,以 F F 为直径的圆与椭圆 E 在第一和第三象限分别交于 M,N 两点.
1 2
且⃗NM⋅⃗AB=2❑√3ac ,则椭圆 E 的离心率为( )
❑√2 ❑√3 ❑√6
A. B. ❑√2 C. D.
2 3 3
二、选择题: 本题共 3 小题, 每小题 6 分, 共 18 分. 在每小题给出的四个选项中, 有多项符合题
目要 求. 全部选对的得 6 分, 部分选对的得部分分, 有选错的得 0 分
9. 某新能源车厂家 2015 - 2023 年新能源电车的产量和销量数据如下表所示
201 201 202
年份 5 2016 2017 8 2019 2020 1 2022 2023
产量(万台) 3.3 7.2 13.1 14.8 18.7 23.7 36.6 44.3 43.0
销量 (万 2.3 5.7 13.6 14.9 15.0 15.6 27.1 29.7 31.6
台)
销量
记“产销率” = ×100%,2015-2023 年新能源电车产量的中位数为 m ,则( )
产量
A. m=18.7
B. 2015 - 2023 年该厂新能源电车的产销率与年份正相关
2
C. 从 2015 -2023 年中随机取 1 年,新能源电车产销率大于 100% 的概率为
9
D. 从 2015 -2023 年中随机取 2 年,在这 2 年中新能源电车的年产量都大于 m 的条件下,这 2
1
年中新能源电车的产销率都大于 70% 的概率为
6
10. 已知动点 M,N 分别在圆 C :(x-1) 2+(y-2) 2=1 和 C :(x-3) 2+(y-4) 2=3 上,动点 P 在 α
1 2
轴上, 则( )
A. 圆 C 的半径为 3
2
B. 圆 C 和圆 C 相离
1 2
C. |PM|+|PN| 的最小值为 2❑√10
D. 过点 P 做圆 C 的切线,则切线长最短为 ❑√3
1
11. 若有穷整数数列 A :a ,a ,⋯a (n≥3) 满足: a -a∈{-1,2}(i=1,2,⋯,n-1) ,且 a =a , =0 ,
n 1 2 n i+1 i 1
则称 A 具有性质 T .则( )
n
A. 存在具有性质 T 的 A
4
2
学科网(北京)股份有限公司B. 存在具有性质 T 的 A
5
C. 若 A 具有性质 T ,则 a ,a ,⋯,a 中至少有两项相同
10 1 2 9
D. 存在正整数 k ,使得对任意具有性质 T 的 A ,都有 a ,a ,⋯,a 中任意两项均不相同
k 1 2 k-1
三、填空题: 本题共 3 个小题, 每小题 5 分, 共 15 分.
1
12. 已知等差数列 {a } 的公差 d≠0 ,首项 a = ,a 是 a 与 a 的等比中项,记 S 为数列
n 1 2 4 2 8 n
{a } 的 前 n 项和,则 S = _________.
n 20
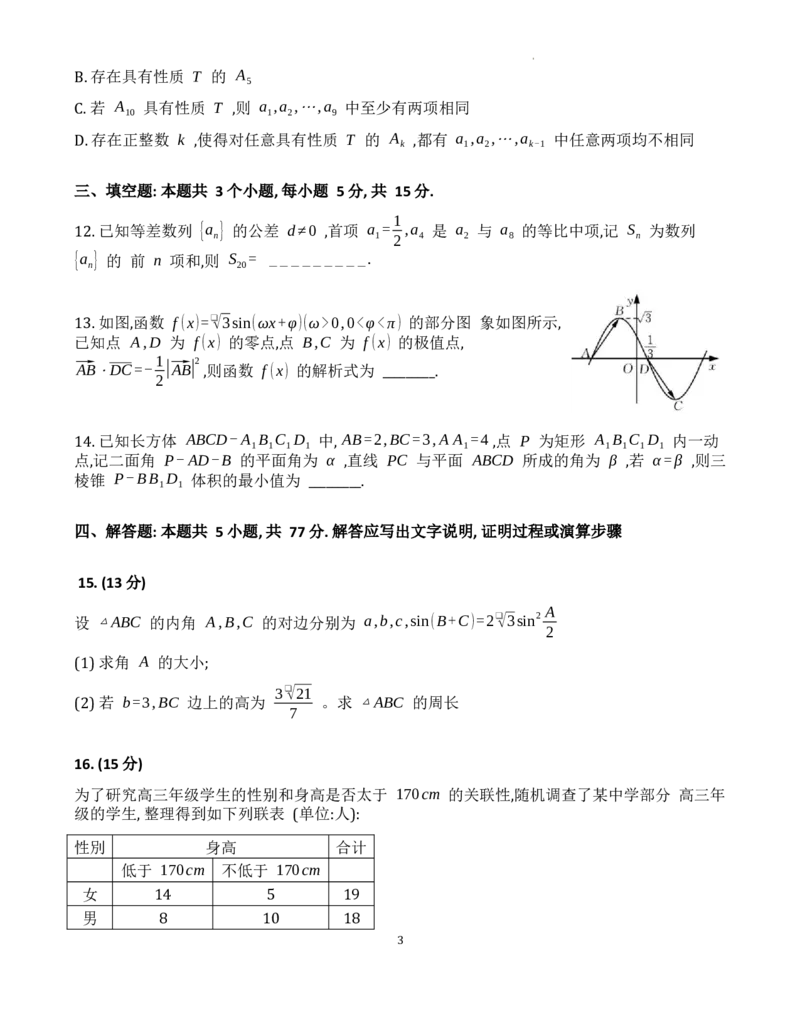
13. 如图,函数 f (x)=❑√3sin(ωx+φ)(ω>0,0<φ<π) 的部分图 象如图所示,
已知点 A,D 为 f (x) 的零点,点 B,C 为 f (x) 的极值点,
1 2
⃗AB⋅DC=- |⃗AB| ,则函数 f (x) 的解析式为 _________.
2
14. 已知长方体 ABCD-A B C D 中, AB=2,BC=3,A A =4 ,点 P 为矩形 A B C D 内一动
1 1 1 1 1 1 1 1 1
点,记二面角 P-AD-B 的平面角为 α ,直线 PC 与平面 ABCD 所成的角为 β ,若 α=β ,则三
棱锥 P-BB D 体积的最小值为 _________.
1 1
四、解答题: 本题共 5 小题, 共 77 分. 解答应写出文字说明, 证明过程或演算步骤
15. (13 分)
A
设 △ABC 的内角 A,B,C 的对边分别为 a,b,c,sin(B+C)=2❑√3sin2
2
(1) 求角 A 的大小;
3❑√21
(2) 若 b=3,BC 边上的高为 。求 △ABC 的周长
7
16. (15 分)
为了研究高三年级学生的性别和身高是否太于 170cm 的关联性,随机调查了某中学部分 高三年
级的学生, 整理得到如下列联表 (单位:人):
性別 身高 合计
低于 170cm 不低于 170cm
女 14 5 19
男 8 10 18
3
学科网(北京)股份有限公司性別 身高 合计
合计 22 15 37
(1) 依据 α=0.1 的独立性检验,能否认为该中学高三年级学生的性别与身高有关联?
(2) 从身高不低于 170cm 的 15 名学生中随机抽取三名学生,设抽取的三名学生中女生人数 为
X ,求 X 的分布列及期望 E(X) .
(3) 若低于 170cm 的 8 名男生身高数据的平均数为 x´ =166.5 ,方差为 s2=9 ,不低于 170cm 的
1
10 名男生身高数据的平均数为 ´y=180 ,方差为 s-2=18 . 请估计该中学男生身高数据的平均数
2
和方差.
n(ad-bc) 2
附: χ2= ,n=a+b+c+d .
(a+b)(c+d)(a+c)(b+d)
α 0.1 0.05 0.01 0.005 0.001
x 2.706 3.841 6.635 7.879 10.828
α
17. (15 分)
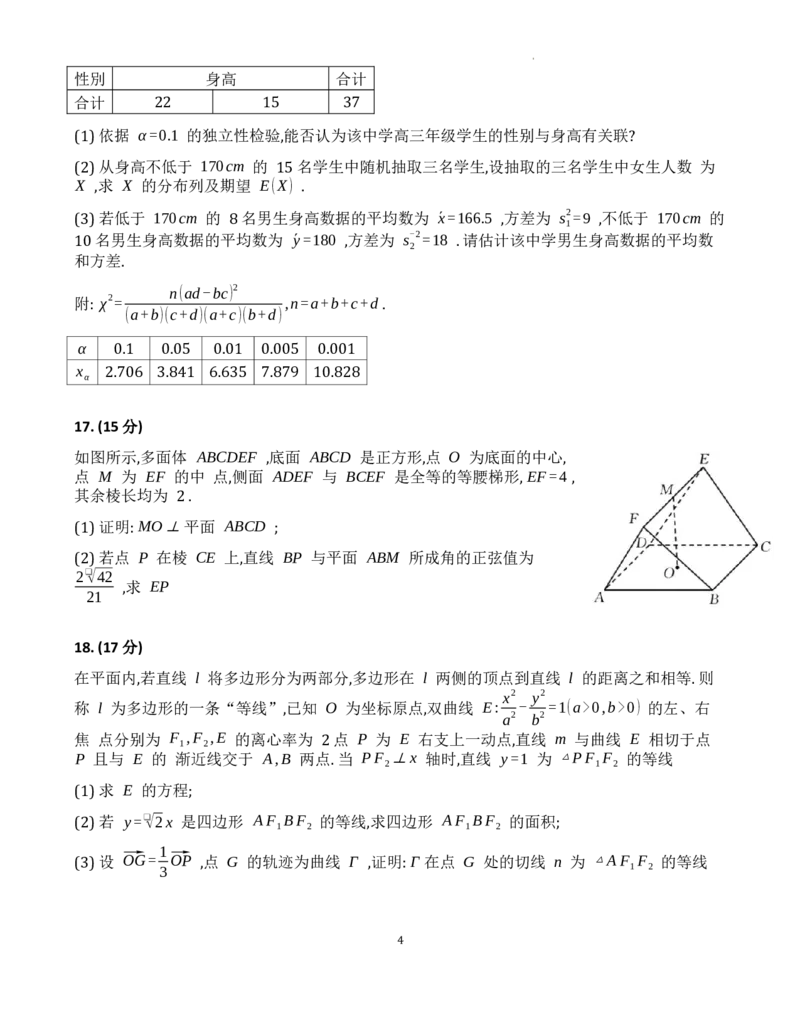
如图所示,多面体 ABCDEF ,底面 ABCD 是正方形,点 O 为底面的中心,
点 M 为 EF 的中 点,侧面 ADEF 与 BCEF 是全等的等腰梯形, EF=4 ,
其余棱长均为 2 .
(1) 证明: MO⊥ 平面 ABCD ;
(2) 若点 P 在棱 CE 上,直线 BP 与平面 ABM 所成角的正弦值为
2❑√42
,求 EP
21
18. (17 分)
在平面内,若直线 l 将多边形分为两部分,多边形在 l 两侧的顶点到直线 l 的距离之和相等. 则
x2 y2
称 l 为多边形的一条“等线”,已知 O 为坐标原点,双曲线 E: - =1(a>0,b>0) 的左、右
a2 b2
焦 点分别为 F ,F ,E 的离心率为 2 点 P 为 E 右支上一动点,直线 m 与曲线 E 相切于点
1 2
P 且与 E 的 渐近线交于 A,B 两点. 当 PF ⊥x 轴时,直线 y=1 为 △PF F 的等线
2 1 2
(1) 求 E 的方程;
(2) 若 y=❑√2x 是四边形 AF BF 的等线,求四边形 AF BF 的面积;
1 2 1 2
1
(3) 设 ⃗OG= ⃗OP ,点 G 的轨迹为曲线 Γ ,证明: Γ 在点 G 处的切线 n 为 △AF F 的等线
3 1 2
4
学科网(北京)股份有限公司19. (17 分)
已知 O 为坐标原点,曲线 f (x)=alnx 在点 P(1,0) 处的切线与曲线 g(x)=ex+b 在点
Q(0,1+b) 处的切线平行,且两切线间的距离为 ❑√2 ,其中 b≥0 .
(1) 求实数 a,b 的值;
(2) 若点 M,N 分别在曲线 y=f (x),y=g(x) 上,求 ∠ONP 与 ∠OMQ 之和的最大值;
(3) 若点 A,B 在曲线 y=f (x) 上,点 C,D 在曲线 y=g(x) 上,四边形 ABCD 为正方形,其面
( 1) 2
积为 S ,证明: S>2 ❑√e-
2
附:ln2 ≈ 0.693.
2024 青岛三模数学试题
数学参考答案及评分标准
一、单项选择题:本题共 8 小题,每小题 5 分,共 40 分.
1-8: CDAC BCBD
二、多项选择题: 本题共 3 小题, 每小题 6 分, 共 18 分.
9. ACD 10. BD 11. ACD
三、填空题: 本题共 3 个小题, 每小题 5 分, 共 15 分.
(π 5π) 10
12. 105 ; 13. f (x)=❑√3sin x+ ; 14. .
2 6 9
四、解答题: 本题共 5 小题, 共 77 分. 解答应写出文字说明, 证明过程或演算步骤
15. (13 分)
解: (1) 因为 A,B,C 为 △ABC 的内角,
所以 sin(B+C)=sin A 1分
5
学科网(北京)股份有限公司A 1-cosA
因为 sin2 = .2分
2 2
A
所以 sin(B+C)=2❑√3sin2 可化为: sin A=❑√3(1-cosA) 3分
2
即 sin A+❑√3cosA=❑√3 4分
( π)
即 2sin A+ =❑√3 5分
3
π (π 4π) π
因为 A+ ∈ , ,解得: A= 6分
3 3 3 3
1 1 3❑√21 ❑√7
(2)由三角形面积公式得 b⋅csin A= × a ,所以 a= c 9分
2 2 7 2
由余弦定理 a2=b2+c2-2bccosA 得: c2+4c-12=0 11分
解得: c=2 或 c=-6 舍去
所以 △ABC 的周长为 5+❑√7 13分
16. (15 分)
解: (1) 根据列联表中的数据, 经计算得到:
100×(15×35-5×45) 2
χ2= ≈3.278>2.706=x 3分
60×40×80×20 0.1
根据小概率值 α=0.1 的独立性检验,可以认为性别与身高有关联 4分
(2)由题可知 X 的可能取值为 0,1,2,3 ,
C3
24
C1C2
45
P(X=0)= 10= ,P(X=1)= 5 10= ,
C3 91 C3 91
15 15
C2C1
20
C3
2
P(X=2)= 5 10= ,P(X=3)= 5 = , 8分
C3 91 C3 91
15 15
所以 X 的分布列为:
X 0 1 2 3
P 24 45 20 2
91 91 91 91
24 45 20 2
所以 E(X)=0× +1× +2× +3× =1 ,
91 91 91 91
6
学科网(北京)股份有限公司所以 X 的数学期望为 1 10分
4 5
(3)由题,18 名男生身高数据的平均数 ´z= ×166.5+ ×180=174 11分
9 9
1 [ 8 10 ]
18 名男生身高数据的方差 s2= ∑(x -´z) 2+∑(y -´z) 2
18 i i
i=1 i=1
1 [ 8 10 ]
= ∑(x -x´+x´ -´z) 2+∑(y -´y+´y-´z) 2
18 i i
i=1 i=1
1 [ 8 10 ]
= ∑(x -x´) 2+8(x´ -´z) 2+∑(y -´y) 2+10(´y-´z) 2
18 i i
i=1 i=1
4 5
= ×[s ❑ 2+(x´ -´z) 2]+ ×[s ❑ 2+(´y-´z) 2]
9 1 9 2
=59
所以, 该中学男生身高数据的平均数约为 174 , 方差约为 59
17. (15 分)
解: (1) 取 AB,CD 中点 K,Q ,连接 FK,KQ,QE ,则 O 为 KQ 的中点,
因为侧面 ADEF 是等腰梯形,所以 EF//AD ,又 KQ//AD ,所以 KQ//EF 1分 又 FK=EQ
,所以四边形 FKQE 为等腰梯形
因为点 M 为 EF 的中点,所以所以 MO⊥KQ .2分
因为 △ABF 是等边三角形,所以 AB⊥FK 3分
又 AB⊥KQ ,所以 AB⊥ 平面 FKQE
所以平面 FKQE⊥ 平面 ABCD 故 MO⊥ 平面 ABCD
(2)在梯形 FKQE 中, EF=4,KQ=2 , FK=EQ=❑√3 ,由勾股定理得 MO=❑√2 , 取 BC 中点 N ,由
(1) 知, OK,ON,OM 两两垂直,以 O 为原点,分别以 OK,ON,OM 所在直线为 x 轴, y 轴, z 轴建
立如图所示 空间直角坐标系,
则 O(0,0,0),M(0,0,❑√2),K(1,0,0),C(-1,1,0),A(1,-1,0)B(1,1,0),E(-2,0,❑√2)
设平面 ABM 的法向量为 ⃗n=(x,y,z),⃗AB=(0,2,0),⃗AM=(-1,1,❑√2) ,
{ ⃗n⋅⃗AB=2y=0
则 ,则令 z=1 ,得 ⃗n=(❑√2,0,1)
⃗n⋅⃗AM=-x+ y+❑√2z=0
7
学科网(北京)股份有限公司设 ⃗CP=λ⃗CE(0≤λ≤1),⃗BP=⃗BC+⃗CP=⃗BC+λ⃗CE=(-2-λ,-λ,❑√2λ) 设直线 BP 与平面 ABM 所
|⃗BP⋅⃗n| |2❑√2| 2❑√42
成角为 θ , 所以 sinθ=|cos<⃗n,⃗BP>|= = = .
|⃗BP|⋅|⃗n| ❑√3❑√4λ2+4λ+4 21
1
解得 λ= (负值舍去),所以点 P 为棱 CE 的中点,所以 EP 的长为 1.
2
18. (17 分)
(
b2
)
解: (1) 由题意知 P c, ,F (-c,0),F (c,0) ,显然点 P 在直线 y=1 的上方,
a 1 2
b2 c
因为直线 y=1 为 △PF F 的等线,所以 -1=2,e= =2,c2=a2+b2 2分 解得 a=1,b=❑√3 ,
1 2 a a
y2
所以 E 的方程为 x2- =1 ·4分
3
y2
(2)设 P(x ,y ) ,切线 m:y- y =k(x-x ) ,代入 x2- =1 得:
0 0 0 0 3
(3-k2)x2+2k(kx - y )x-(k2x2+ y2-2kx y +3)=0,
0 0 0 0 0 0
所以 Δ=[2k(kx - y )] 2 +4(3-k2)(k2x ❑ 2+ y ❑ 2-2kx y +3)=0 ,
0 0 0 0 0 0
该式可以看作关于 k 的一元二次方程 (x ❑ 2-1)k2-2x y k+ y ❑ 2+3=0 ,
0 0 0 0
x y x y 3x
k= 0 0 = 0 0 = 0
y y
所以 x2 0 -1 ( 1+ y2 0 ) -1 y 0 ,即 m 方程为 x 0 x- 3 0 =1(*)
3
当 m 斜率不存在时,也成立 6分
渐近线方程为 y=±❑√3x ,不妨设 A 在 B 上方,
1 1 1 1
x = ,x = x +x = + =2x
联立得 A y B y ,故 A B y y 0 ,
x - 0 x + 0 x - 0 x + 0
0 ❑√3 0 ❑√3 0 ❑√3 0 ❑√3
所以 P 是线段 AB 的中点 .7分
因为 F ,F 到过 O 的直线距离相等,则过 O 点的等线必满足: A,B 到该等线距离相等 且分居
1 2
两侧,所以该等线必过点 P ,即 OP 的方程为 y=❑√2x ,
{ y=❑√2x
由 y2 ,解得: P(❑√3,❑√6) .9分
x2- =1
3
8
学科网(北京)股份有限公司❑√3 3
y =❑√3x = = =❑√6+3
所以 A A y ❑√3x - y ,
x - 0 0 0
0 ❑√3
❑√3 -3
y =-❑√3x =- = =❑√6-3
所以 B B y ❑√3x + y ,
x + 0 0 0
0 ❑√3
1
所以 |y - y |=6 ,所以 S = |F F |⋅|y - y |=2|y - y |=12 11分
A B ABCD 2 1 2 A B A B
1
(3)设 G(x,y) ,由 ⃗OG= ⃗OP ,所以 x =3x,y =3 y ,
3 0 0
故曲线 Γ 的方程为 9x2-3 y2=1(x>0) 12分
9x 3 y y y y 1
由 (*) 知切线为 n 为 0 x- 0 =1 ,即 x x- 0 = 即 3x x- y y-1=0 13分
3 3 0 3 3 0 0
易知 A 与 F 在 n 的右侧, F 在 n 的左侧,分别记 F ,F ,A 到 n 的距离为 d ,d ,d , 由
2 1 1 2 1 2 3
1 1 ❑√3
x = ,y =❑√3⋅ =
(2) 知 A y A y y ,
x - 0 x - 0 x - 0
0 ❑√3 0 ❑√3 0 ❑√3
y 2y
| | | |
3x -❑√3 y -x + 0 2x - 0
| 3x ❑√3 y | 0 0 0 ❑√3 0 ❑√3
0 - 0 -1
所以 y y y y
x - 0 x - 0 x - 0 x - 0
0 ❑√3 0 ❑√3 0 ❑√3 0 ❑√3
2
d = = = =
3 ❑√9x2+ y2 ❑√9x2+ y2 ❑√9x2+ y2 ❑√9x2+ y2
0 0 0 0 0 0 0 0
|-6x -1| 6x +1 |6x -1| 6x -1
由 x ≥1 得 d = 0 = 0 ,d = 0 = 0 15分
0 1 ❑√9x2+ y2 ❑√9x2+ y2 2 ❑√9x2+ y2 ❑√9x2+ y2
0 0 0 0 0 0 0 0
6x -1 2 6x +1
因为 d +d = 0 + = 0 =d ,
2 3 ❑√9x2+ y2 ❑√9x2+ y2 ❑√9x2+ y2 1
0 0 0 0 0 0
所以直线 n 为 △AF F 的等线 .17分
1 2
19. (17 分)
a
解: (1) 因为 f'(x)= ,所以 f'(1)=a ,又因为 g'(x)=ex ,所以 g'(0)=1 ,
x
解得 a=1 1 分
所以 f (x) 在 (1,0) 处的切线方程为: y=a(x-1)=x-1 ,
9
学科网(北京)股份有限公司所以 g(x) 在 (0,1+b) 处的切线方程为: y=x+1+b ,
|2+b| 2+b
所以 ❑√2= = ,解得 b=0 3分
❑√2 ❑√2
(2)(法一) 由(1)知: P(1,0),Q(0,1) ,记直线 NP,ON 的倾斜角分别为 α,β ,斜率分 别为
k ,k ,所以 ∠ONP=α-β ,设 N(x,ex),x≠0 且 x≠1 ,
1 2
ex ex
-
k -k x-1 x ex
所以 tan∠ONP=tan(α-β)= 1 2 = = 5分
1+k k ex ex x2-x+e2x
1 2 1+ ⋅
x-1 x
ex ex(x2-3x+1-e2x)
令 m(x)= (x≠0,x≠1) ,则 m'(x)= ,
x2-x+e2x (x2-x+e2x) 2
当 x>0 时,设函数 n(x)=ex-x-1 ,则 n'(x)=ex-1>0 ,
所以 n(x) 在 (0,+∞) 单调递增,所以 n(x)≥n(0)=0 ,即 ex≥x+1>1 ,
所以 x2-3x+1-e2x≤x2-3x+1-(x+1) 2=-5x<0 ,
1
所以 m(x) 在 (0,1),(1,+∞) 均单调递减,且 m(1)= <1 6分
e
当 x<0 时, x2-3x+1-e2x>1-e2x>0 ,所以 m(x) 在 (-∞,0) 单调递增,
1
所以 m(x)0) 的零点为 x ,
1 1
1 1 1 √ 1
因为 h'(x)=ex+ -2≥x+1+ -2=x+ -1≥2❑ x⋅ -1=1>0 ,
x x x x
所以 h(x) 在 (0,+∞) 单调递增,
(1)
故 h =❑√e-ln2-1<❑√e-0.69-1=❑√e-1.69<0,h(1)=e-2>0 ,
2
1
所以 0) ,则 φ'(x)=ex-1>0 ,所以 φ(x) 在 (0,+∞) 单调递增,
所以 S=[❑√2(x -x )] 2 =2(ex 1-x ) 2 >2 ( ❑√e- 1) 2 17分
2 1 1 2
12
学科网(北京)股份有限公司