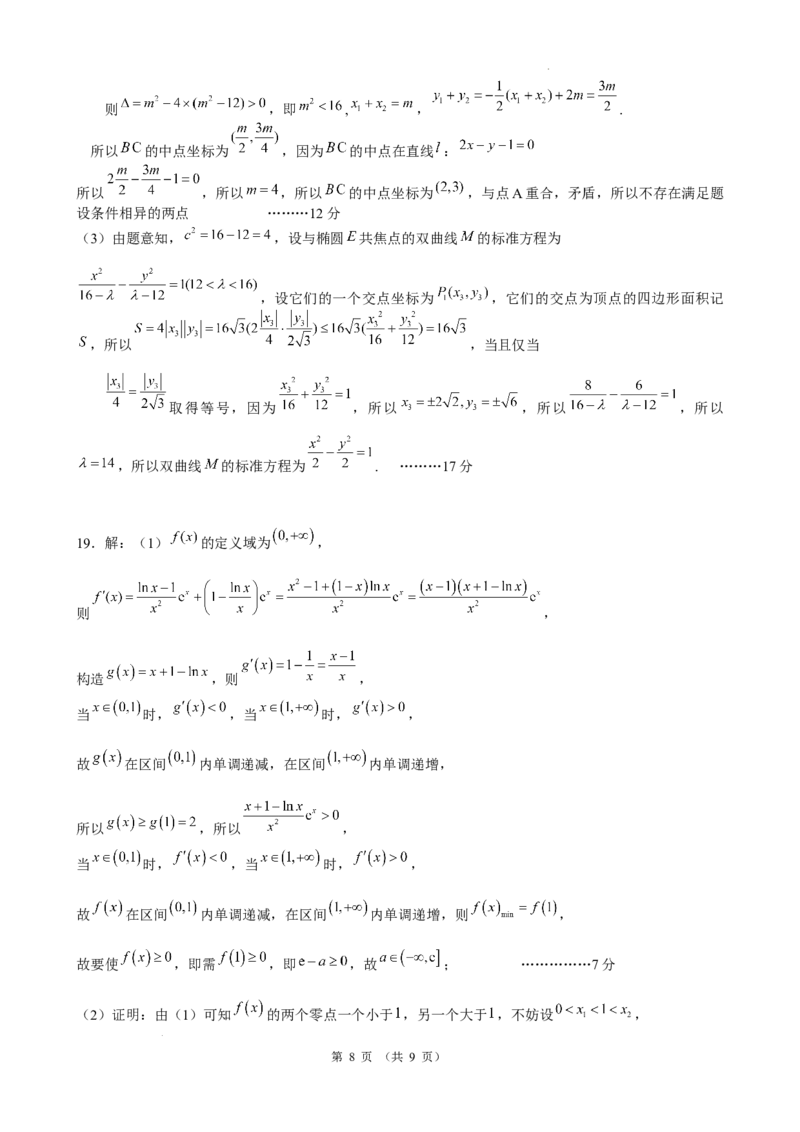文档内容
昆明一中 2024 届高三第 8 次联考
数学参考答案
命题、审题组教师 杨昆华 彭力 李文清 李春宣 丁茵 王在方 张远雄 李露 陈泳序 杨耕耘
一、选择题
题号 1 2 3 4 5 6 7 8
答案 C A A B D B D A
1.解析:因为 ,选C.
2.解析:因为 ,所以 ,所以 ,选A.
3.解析:设 与 夹角为 ,因为 ,所以
,当 时, 取最大值3,选A.
4.解析:因为 ,所以 点到圆心的距离恒为 ,所以点 的轨迹方程是以 为圆心,
为半径的圆,即 ,选B.
5.解析:过点 作 ,交 于点 ,
因为 , , , , 平面 ,所以 平面 ,
又 ,所以 平面 ,且 ,可得 ,
因为 , 分别为 , 的中点,则 ,
所以, , ,
因此 .
第 1 页 (共 9 页)
学科网(北京)股份有限公司选D.
6.解析:因为 ,
又因为 能被 整除,所以 能被13整除,所以 ,选B.
7.解析:为 ,所以方差大于 ,因此不能出现点数 6,因为 ,
, ,则其余的点数 都有可能出现,选D.
8.解析:设 ,则 ,得 ,则 在 上单调递增,在
上单调递减, , ,则 ,又 ,得 ,
所以 ,选A.
二、多选题
题号 9 10 11
答案 BD BC ABC
9.解析:因为分数在 内的频率为 ,所以第三组
的频数为 ,故A错误;
因为众数的估计值是频率分布直方图中最高矩形底边的中点的横坐标,从图中可看出众数的估计值为
分,故B 正确;
因为 , ,所以中位数位于
内,设中位数为 ,则 ,解得 ,所以中位数的估计值为 分,故C错误;
样 本 平 均 数 的 估 计 值 为
分,故D正确,选B D.
10.解析:对于A,已知 ,若 ,则需 ,易知当
与 重合时, 平面 , 平面 ,所以 ,故
可能成立,故A错误;
对于B,假设直线 与平面 垂直,又因为 ,则 ,显然
第 2 页 (共 9 页)
学科网(北京)股份有限公司不合题意,因此假设不成立,即直线 与平面 不可能垂直,故B正确;
对于C,当 为 的中点时,连接 , , ,可知直线 平面 ,则平面 为平面
z
,即平面 截正四棱柱所得截面多边形为△ ,所以截面多边
形的周长为 ,故C正确;
对于D, 以 为原点,直线 , , 分别为 , , 轴建立
o
y
x
如图所示坐标系,以题意可知 , ,则 ,设
,平面 的一个法向量为 ,所以
,又 ,所以 ,故D错误.
选BC
11.解析:令 ,得 ;令 ,则 ,得 ,A 对;令
,则 ,得 ,B对;
由于 ,
令 ,则 ,令 ,得 ,令 ,则 ,所以
既是奇函数又是偶函数,且 ,则 ,C对D错,选ABC.
三、填空题
12 . 解 析 : 抛 物 线 的 焦 点 为 , 准 线 方 程 为 , 根 据 题 意 可 得 ,
.
13.解析:由题意, ,得 ,令 ,则 ,
第 3 页 (共 9 页)
学科网(北京)股份有限公司得 ,所以 .
14.解析:设长方体 的高为 , 若 ,则 , ,则 ,若
A B C D
1 1 1 1
要长方体体积最大,则平面 内接于长方体,如图
可得 ,即 ,则 ,
所以长方体 的体积为
,
设 ,其中 ,则 ,令 ,得 ,当 时,
, 在 上单调递增;当 时, , 在 上单调递减,所以函数
在 处取得极大值,即最大值,则 ,因此该长方体的体积的最大值为 .
四、解答题
15.解:(1)选择①:因为 ,
所以 ,
,
两式相减得 ,
即 ,
因为 ,所以
所以数列 是以 为首项, 为公差的等差数列,
故 . ………6分
第 4 页 (共 9 页)
学科网(北京)股份有限公司选择②:因为 ,所以 ,
所以 ,所以 ,又因为 , ,所以 ,
所以数列 是以 为首项, 为公差的等差数列,
所以 . ………6分
选择③:因为 ,
又因为 ,所以 ,
所以 ,
又因为 ,所以 ,
所以 是以 为首项, 为公差的等差数列,所以 ,
所以 ,所以 ,检验 时也满足,
所以 . ………6分
(2)由(1)知: ,所以 ,
因为 ,
所以 ,
所以 ,
所以 . ………13分
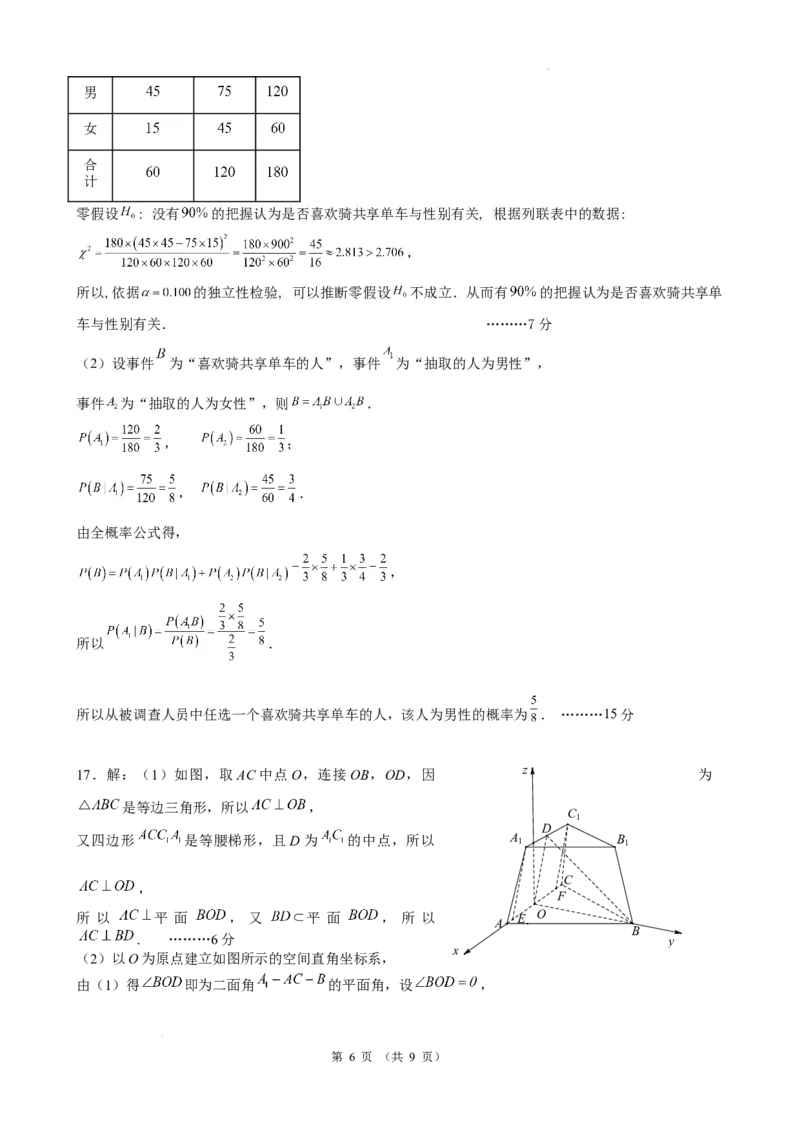
16.解:(1)由表格可得 列联表如下.
是否喜欢骑共享单车
性
合计
别
不喜欢 喜欢
第 5 页 (共 9 页)
学科网(北京)股份有限公司男
女
合
计
零假设 : 没有 的把握认为是否喜欢骑共享单车与性别有关, 根据列联表中的数据:
,
所以,依据 的独立性检验, 可以推断零假设 不成立.从而有 的把握认为是否喜欢骑共享单
车与性别有关. ………7分
(2)设事件 为“喜欢骑共享单车的人”,事件 为“抽取的人为男性”,
事件 为“抽取的人为女性”,则 .
, ;
, .
由全概率公式得,
,
所以 .
所以从被调查人员中任选一个喜欢骑共享单车的人,该人为男性的概率为 . ………15分
17.解:(1)如图,取AC中点O,连接OB,OD,因 z 为
是等边三角形,所以 ,
C
1
D
又四边形 是等腰梯形,且D为 的中点,所以 A 1 B 1
C
,
F
所 以 平 面 , 又 平 面 , 所 以 E O
A
B
. ………6分 y
x
(2)以O为原点建立如图所示的空间直角坐标系,
由(1)得 即为二面角 的平面角,设 ,
第 6 页 (共 9 页)
学科网(北京)股份有限公司作 于E,由 可得 ,
,故 ,
作 于F,同理可得 ,所以 ,
从而 , , , , , ,所以
,
,
,
设平面 的法向量为 ,则 ,所以 ,
从而
即 ,化简得: ,
解得: 或 (舍)
所以二面角 的大小为 . ………15分
18.解:(1)设 的平分线与 轴交于点 ,由题意知, , ,A
所以 ,所以 ,所以 ,所以 ,所以直线 的方程为
………5分
(2)假设存在两点 关于直线 对称,则 ,所以 ,
设直线 的方程为 ,联立 ,得 ,
第 7 页 (共 9 页)
学科网(北京)股份有限公司则 ,即 , , .
所以 的中点坐标为 ,因为 的中点在直线 :
所以 ,所以 ,所以 的中点坐标为 ,与点A重合,矛盾,所以不存在满足题
设条件相异的两点 ………12分
(3)由题意知, ,设与椭圆 共焦点的双曲线 的标准方程为
,设它们的一个交点坐标为 ,它们的交点为顶点的四边形面积记
,所以 ,当且仅当
取得等号,因为 ,所以 ,所以 ,所以
,所以双曲线 的标准方程为 . ………17分
19.解:(1) 的定义域为 ,
则 ,
构造 ,则 ,
当 时, ,当 时, ,
故 在区间 内单调递减,在区间 内单调递增,
所以 ,所以 ,
当 时, ,当 时, ,
故 在区间 内单调递减,在区间 内单调递增,则 ,
故要使 ,即需 ,即 ,故 ; ……………7分
(2)证明:由(1)可知 的两个零点一个小于 ,另一个大于 ,不妨设 ,
第 8 页 (共 9 页)
学科网(北京)股份有限公司因为 ,构造函数 , ,则 ,
故 在 单调递增,则由 ,
则由 可知 ,即 ,
即 ,即 ,
要证 ,即证 ,即证 ,
构造函数 ,则 ,
则 ,
故 在区间 内单调递减,则 ,即 ,
特别地,取 ,则有 ,即
即 ,故 . ……………17分
第 9 页 (共 9 页)
学科网(北京)股份有限公司