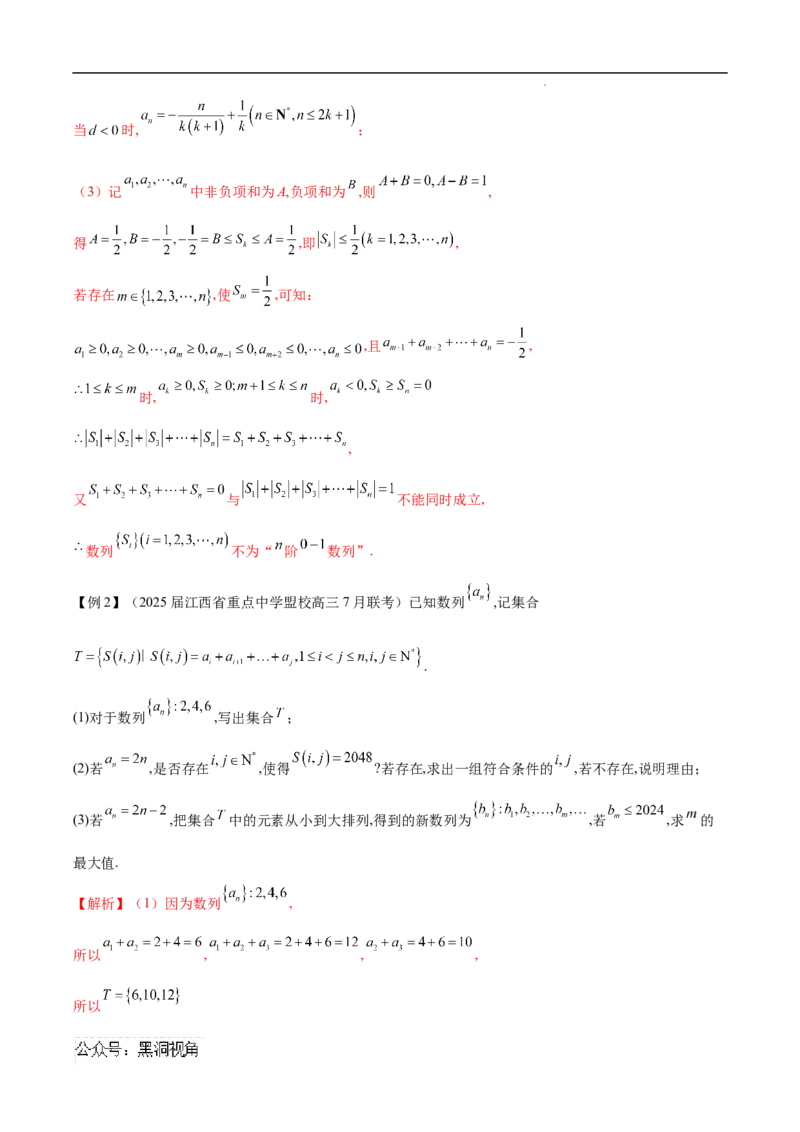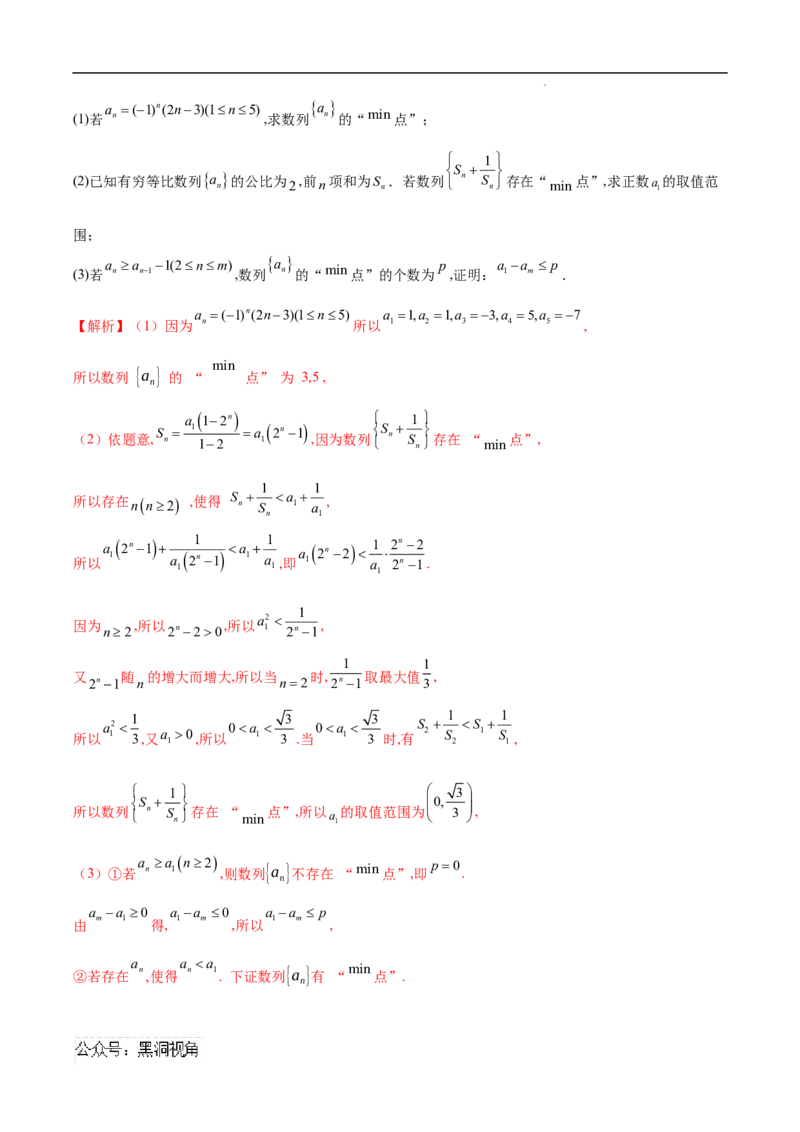专题09数列新定义问题（原卷版）_2024-2025高三（6-6月题库）_2025年02月试卷_02272025年高考数学压轴大题必杀技系列·数列

专题 9 数列新定义问题 新高考在试题形式、试卷结构、难度调控等方面深化改革,数列解答题的难度增加,作为压轴题出现 的概率变大, 为面对拔尖创新人才选拔培养等新要求,新高考试卷增加了新定义问题,数列是新定义问题的 重要载体,本专题总结数列中新定义问题的常见类型,供大家参考. （一）数列新定义问题的特点及求解策略 1.新定义试题通过新定义一个数学对象或数学运算,以此为基础为学生搭建思维平台,设置试题.该题型形 式新颖,考查功能显著,主要表现在四个方面：通过新定义创设数学新语境和话语体系；通过新情境搭建 试题框架,创设解题条件；通过新设问设置思维梯度,逐步深入,准确区分不同层次的学生；通过解题过程 展现学生数学思维和探究过程,实现对分析、推理、判断、论述等关键能力的考查. 2.通过给出一个新的定义,或约定一种新的运算,或给出几个新模型来创设新问题的情景,要求在阅读理解的 基础上,依据题目提供的信息,联系所学的知识和方法,实心信息的迁移,达到灵活解题的目的. 3.遇到数列新定义问题,应耐心读题,分析新定义的特点,弄清新定义的性质,按新定义的要求,“照章办事”,逐 条分析、运算、验证,使得问题得以解决. 4. 类比“熟悉数列"的研究方式,用特殊化的方法研究新数列,向“熟悉数列"的性质靠. 【例1】（2025届湖北省武汉市江汉区高三7月新起点摸底）若有穷数列 满足： 且 , 则称其为“ 阶 数列”. (1)若“6阶 数列”为等比数列,写出该数列的各项； (2)若某“ 阶 数列”为等差数列,求该数列的通项 （ ,用 表示）； (3)记“ 阶 数列” 的前 项和为 ,若存在 ,使 ,试问：数列 学科网（北京）股份有限公司能否为“ 阶 数列”？若能,求出所有这样的数列 ；若不能,请说明理由. 【解析】（1）设 成公比为 的等比数列,显然 , 则有 ,得 ,解得 , 由 ,得 ,解得 , 所以数列 或 为所求； （2）设等差数列 的公差为 , , ,即 ,当 时,矛盾, 当 时, , ,即 ,由 得 ,即 , , 当 时,同理可得 ,即 , 由 得 ,即 , , 综上所述,当 时, , 学科网（北京）股份有限公司当 时, ； （3）记 中非负项和为A,负项和为 ,则 , 得 ,即 , 若存在 ,使 ,可知： ,且 , 时, 时, , 又 与 不能同时成立, 数列 不为“ 阶 数列”. 【例2】（2025届江西省重点中学盟校高三7月联考）已知数列 ,记集合 . (1)对于数列 ,写出集合 ； (2)若 ,是否存在 ,使得 ?若存在,求出一组符合条件的 ,若不存在,说明理由； (3)若 ,把集合 中的元素从小到大排列,得到的新数列为 ,若 ,求 的 最大值. 【解析】（1）因为数列 , 所以 , , , 所以 学科网（北京）股份有限公司（2）假设存在 ,使得 ,则有 , 由于 与 奇偶性相同,所以 与 奇偶性不同, 又因为 , ,所以 中必有大于等于3的奇数因子 这与 无1以外的奇数因子矛盾,故不存在 ,使得 ； （3）由题意得 , 当 , 时, , 除 , 外, , , 其中 与 一奇一偶,则 能拆成奇数与偶数之乘积, 在正偶数中,只有 无法拆成一个大于2的奇数与一个不小于2的偶数之乘积, 又 中的元素均为偶数,故 , 故2至2024偶数中除去4,8,16,32,64,128,256,512,1024, 所以 ,故 的最大值为 ． （二）定义一类新数列 此类问题,通常把满足某些条件的数列定义为一类新数列,然后利用这些条件求解所给问题. 【例3】（2024届新疆部分学校高三4月二模）我们把满足下列条件的数列 称为 数列： ①数列 的每一项都是正偶数； ②存在正奇数m,使得数列 的每一项除以m所得的商都不是正偶数． (1)若a,b,c是公差为2的等差数列,求证：a,b,c不是 数列； (2)若数列 满足对任意正整数p,q,恒有 ,且 ,判断数列 是否是 数列,并证 学科网（北京）股份有限公司明你的结论； (3)已知各项均为正数的数列 共有100项,且对任意 ,恒有 ,若数列 为 数列,求满足条件的所有两位数k 值的和． 【解析】（1）若 a,b,c 是 数列, 则 a,b,c 都是正偶数, 设 ,则 若 , 则 除以 3 为 , 是正偶数, 与题中条件 (2) 矛盾, 若 , 则 除以 3 为 , 是正偶数, 与题中条件 (2) 矛盾, 若 , 则 除以 3 为 , 是正偶数, 与题中条件 (2) 矛盾, 所以 a,b,c 不是 数列. （2）在 中, 令 , 得 , 所以数列 是首项为 8 , 公比为 8 的等比数列, 所以 , 因为 是正偶数, 所以数列 的每一项都满足题中条件 (1), 因为 , 能被 7 整除, 所以 除以 7 的余数为 1 , 即数列 的每一项被 7 除余 1 , 一定不是正整数, 所以一定不是正偶数, 即数列 的每一项都满足题中条件(2), 学科网（北京）股份有限公司所以数列 是 数列. （3）因为 , 所以 , , 得 . 因为 , 所以 , , 得 . 因为 , 所以 . 在 中, 分别令 , 得 , 所以数列 是首项为 , 公差为 的等差数列, 所以 . 若数列 是 数列, 则 是正偶数, 除以 111 所得的商都不是正偶数, 学科网（北京）股份有限公司因为 , 且 , 所以当 为 3 或 37 的正偶数倍时, 数列 不是 数列, 所以满足条件的所有两位数 值的和为 . 【例4】（2024届江苏省江阴市成化高级中学高三下学期调研）如果一个数列从第二项起,每一项与它前一 项的比都大于3,则称这个数列为“ 型数列”. (1)若数列 满足 ,判断 是否为“ 型数列”,并说明理由； (2)已知正项数列 为“ 型数列”, ,数列 满足 ,n∈N*, 是等比数列,公比为正整 数,且不是“ 型数列”, ①求证：数列 为递增数列； ②求数列 的通项公式. 【解析】（1） 不满足“ 型数列”定义,数列 不是“ 型数列”； （2）①∵正项数列 为“ 型数列”, ∴数列 为递增数列 ②设数列 的公比为 , ,又因为数列 不是“ 型数列”,可得 可得 ,即得 ； 学科网（北京）股份有限公司又数列 为“ 型数列”,可得 ； 由①知 为递增数列,因此当 趋近于正无穷大时, 趋近于 ,即可得 ； 综上可得 ,即 ,可得 ； 所以数列 是以 为首项,公比为 的等比数列； 即可得 ,可得 ；所以数列 的通项公式为 . （三）定义一个新运算 此类问题一般是定义一个临时的运算法则,然后按照这个运算法则去求解,求解的关键是理解所给的运算法 则,然后“按章办事”. a  S a 5 b  【例5】(2024届天津市滨海高考模拟检测)已知等差数列 n 的前 n 项和为 n, 3 ,S =63,数列 n 是公 9 b b b 14 bbb 64 比大于1的等比数列,且 1 2 3 , 1 2 3 ． a  b  (1)求 n , n 的通项公式； a  b  b a a b (2)数列 n , n 的所有项按照“当 n 为奇数时, n放在 n的前面；当 n 为偶数时, n放在 n的前面”的要求 c  b a a b b a a c  T 进行“交叉排列”,得到一个新数列 n ： 1, 1, 2, 2, 3, 3, 4,…,求数列 n 的前7项和 7及前4n+3项和 T ； 4n+3 n a 2d 2n1n2 d  i n1i d  (3)是否存在数列 n ,满足等式 i1 成立,若存在,求出数列 n 的通项公式,若不存在, 请说明理由． d a 5 【解析】（1）设等差数列{a }的公差为 , 3 ,S =63 n 9 9a a  S  1 9 9a 63 可知 9 2 5 ,所以a =7． 5 学科网（北京）股份有限公司a 5 a a n3d n2 又 3 ,所以数列{a }的公差 d 1 ,所以 n 3 , n q b b b 14 bbb 64 设等比数列{b }的公比为 , 1 2 3 , 1 2 3 ． n b bqbq2 14 b3q3 64 bq4 2q25q20 所以 1 1 1 , 1 ．得到 1 ,联立得 1 q 解得 q=2 或 2 （舍去）,代入bq4中,解得b 2 1 1 b 2n 得数列{b }的通项公式为 n ． n T b a a b b a a a a a a b b b 32 （2）由题意 7 1 1 2 2 3 3 4 1 2 3 4 1 2 3 T b a a b b a a b b a a b b a a 4n3 1 1 2 2 3 3 4 4 2n1 2n1 2n 2n 2n1 2n1 2n2 a a a a a a a a b b b b b b  1 2 3 4 2n1 2n 2n1 2n2 1 2 3 2n1 2n 2n1 a a 2n2 2  122n1  1 2n 2 2  12 =4n+1+2n2+9n+5 n （3）由已知 a 2d 2n1n2得 ① i n1i d 2d 3d nd 2n1n2 i1 n n1 n2 1 d 2d 3d n1d 2nn1 当 n2 时, n1 n2 n3 1 ②, d d d d 2n1 ①②两式相减得： n n1 n2 1 , n1 d 211121 d d d d 2n1 当 时, 1 也符合 n n1 n2 1 ③ d d d d 2n1 nN* 所以 n n1 n2 1 ,对于 都成立． n2 d d d 2n11 又当 时 n1 n2 1 ④成立 d 2n1 n1 d 2n1 ③④两式相减得： n ,经检验 也符合故存在 n ． （四）定义数列的新性质 此类问题,通常是总结出数列的一个性质,然后判断所给数列是否具有此性质,或根据数列的该性质去求解或 验证某些结论. 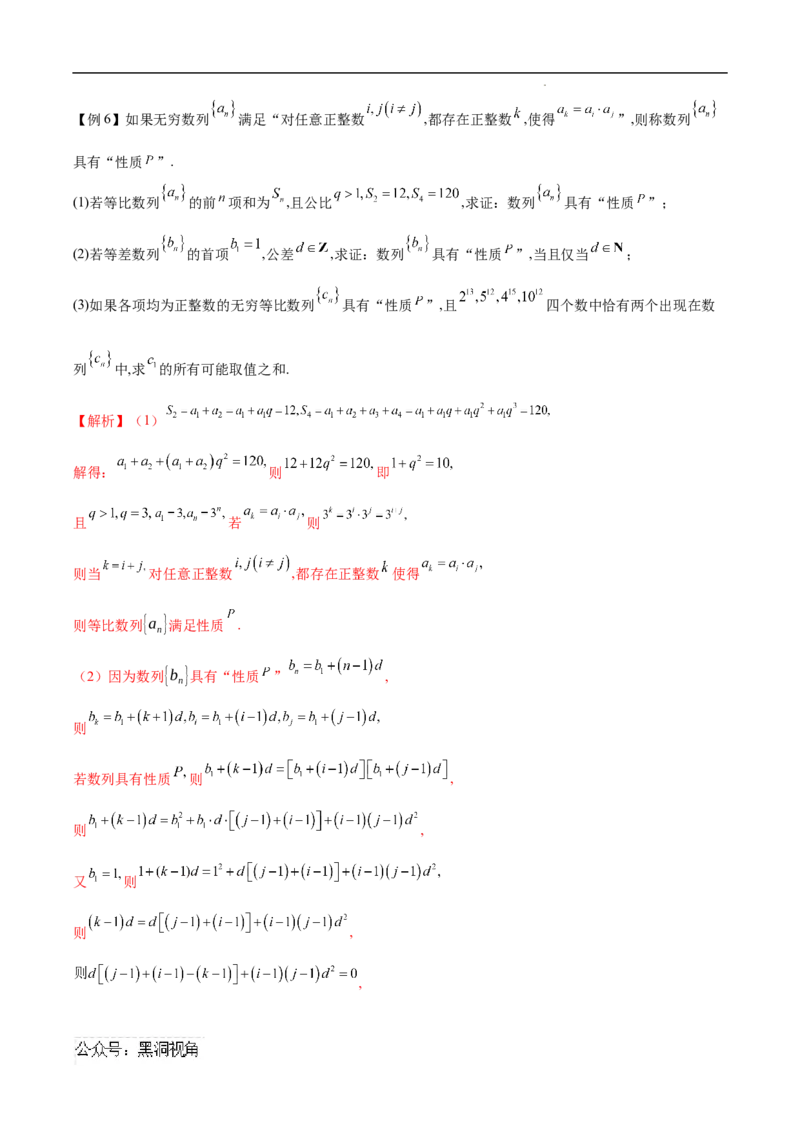学科网（北京）股份有限公司【例6】如果无穷数列 满足“对任意正整数 ,都存在正整数 ,使得 ”,则称数列 具有“性质 ”. (1)若等比数列 的前 项和为 ,且公比 ,求证：数列 具有“性质 ”； (2)若等差数列 的首项 ,公差 ,求证：数列 具有“性质 ”,当且仅当 ； (3)如果各项均为正整数的无穷等比数列 具有“性质 ”,且 四个数中恰有两个出现在数 列 中,求 的所有可能取值之和. 【解析】（1） 解得： 则 即 且 若 则 则当 对任意正整数 ,都存在正整数 使得 则等比数列{a }满足性质 . n （2）因为数列{b }具有“性质 ” , n 则 若数列具有性质 则 , 则 , 又 则 则 , , 学科网（北京）股份有限公司则 , 又 则当 时上式成立, 当 时. , 则 因为 则 时,则 则 则 则 反之,若 则 则上面各式成立,则数列{b }具有“性质 ” n 综上数列{b }具有“性质 ”,当且仅当 . n （3）从 这四个数中任选两个,共有以下6种情况： , ； , ； , ; , ; , ; , . ①对于 , 因为 为正整数,可以认为{a }是等比数列中的项, ,首项的最小值为1. n 下面说明此数列具有性质P： = , = ,任取 , ,则 , 为正整数,因此此数列具有性质P, ②对于 , .因为 为正整数,认为是等比数列{a }中的项, , n 首项的最小值为 ,下面说明此数列不具有性质P： , ,若 不为等比数列{a }中的项, n 因此此数列不具有性质P,同理可得 , ； , ； , ； , 每组所在等比数列{a }不具有“性质P’’ n 学科网（北京）股份有限公司（五）定义一个新情景 此类问题通过创设数学新语境和话语体系,通过新情境搭建试题框架. 【例7】（2025届湖北省武汉市硚口区部分高中高三起点考试）定义：在一个有穷数列的每相邻两项之间 插入这两项的和,形成新的数列,我们把这样的操作称为该数列的一次“和扩充”,例如：数列 经过第一 次“和扩充”后得到数列 ；第二次“和扩充”后得到数列 .设数列 经过 次 “和扩充”后得到的数列的项数为 ,所有项的和为 . (1)若 ,求 ； (2)若 ,求正整数 的最小值； (3)是否存在数列 ,使得数列 为等比数列？请说明理由. 【解析】（1） ,第一次“和扩充”后得到数列 , 第二次“和扩充”后得到数列 , , ； （2）数列经每一次“和扩充”后是在原数列的相邻两项中增加一项, 数列 经过 次“和扩充”后得到的数列的项数为 , 则经第 次“和扩充”后增加的项数为 , 所以 ,所以 , 其中数列 经过1次“和扩充”后,得到 , 故 ,故 是首项为4,公比为2的等比数列, 所以 ,故 ,则 ,即 , 学科网（北京）股份有限公司又 ,解得 ,最小值为10； （3）因为 , ,依次类推, , 故 , 若使 为等比数列,则 或 . （六）具有高等数学背景的数列新定义 数列的极限、收敛性及子数列等具有高等数学背景的数列问题,常出现在高中模拟试卷中. 【例8】（湖北省宜荆荆高三下学期适应性考试）龙泉游泳馆为给顾客更好的体验,推出了A和B两个套餐 服务,顾客可选择A和B两个套餐之一,并在App平台上推出了优惠券活动,下表是该游泳馆在App平台10天 销售优惠券情况． 日期t 1 2 3 4 5 6 7 8 9 10 销售量 千张 1.9 1.98 2.2 2.36 2.43 2.59 2.68 2.76 2.7 0.4 经计算可得： . (1)因为优惠券购买火爆,App平台在第10天时系统出现异常,导致当天顾客购买优惠券数量大幅减少,已知销 售量y和日期t呈线性关系,现剔除第10天数据,求y关于t的经验回归方程 结果中的数值用分数表示 ； (2)若购买优惠券的顾客选择A套餐的概率为 ,选择B套餐的概率为 ,并且A套餐可以用一张优惠券,B套 餐可以用两张优惠券,记App平台累计销售优惠券为n张的概率为 ,求 ； 学科网（北京）股份有限公司(3)记（2）中所得概率 的值构成数列 . ①求 的最值； ②数列收敛的定义：已知数列 ,若对于任意给定的正数 ,总存在正整数 ,使得当 时, , （ 是一个确定的实数）,则称数列 收敛于 .根据数列收敛的定义证明数列 收敛． 参考公式： . 【解析】（1）解：剔除第10天的数据,可得 , , 则 , 所以 , 可得 ,所以 . （2）解：由题意知 ,其中 , 所以 ,又由 , 所以 是首项为1的常数列,所以 所以 ,又因为 , 所以数列 是首项为 ,公比为 的等比数列, 学科网（北京）股份有限公司故 ,所以 . （3）解：①当 为偶数时, 单调递减, 最大值为 ； 当 为奇数时, 单调递增,最小值为 , 综上可得,数列 的最大值为 ,最小值为 . ②证明：对任意 总存在正整数 , 其中 表示取整函数 , 当 时, ,所以数列 收敛. （七）集合背景中的数列新定义问题 不少数列问题,常使用集合语言进行“包装”,求解此类问题的关键是把问题还原为数列问题. 【例9】已知数集 （ ）,若对任意的 （ ）, 与 两数中至少有一个属于A,则称数集A具有性质P． (1)分别判断数集B= 与数集C= 是否具有性质 ,并说明理由； (2)若数集A具有性质P． ①当 时,证明 ,且 成等比数列； ②证明： ． 【解析】（1）数集 具有性质 , 不具有性质 ,理由如下： 因为 , , , , , 都属于数集 ,所以 具有性质 ； 因为 , 都不属于数集 ,所以 不具有性质 ． 学科网（北京）股份有限公司（2）①当 时, , ． 因为 ,所以 , ,所以 与 都不属于A, 因此 , ,所以 ． 因为 ,且 ,所以 , 且 ,所以 ,所以 成等比数列． ②因为 具有性质 ,所以 , 至少有一个属于A, 因为 ,所以 , ,因此 , ． 因为 ,所以 （ ）, 故当 时, , ,（ ）, 又因为 , 则 , , , , , 可得 , 所以 . 【例10】（2024届湖南省长沙市长郡中学高三下学期二模）集合论在离散数学中有着非常重要的地位.对 于非空集合A和B,定义和集 ABab aA,bB ,用符号 d(AB) 表示和集AB内的元素个数. A1,3,5 B1,2,6 C 1,2,6,x AB AC x (1)已知集合 , , ,若 ,求 的值； 学科网（北京）股份有限公司  (2)记集合 A n 1,2,  ,n , B n  2,2 2,  ,n 2 , C n  A n B n, a n为C n 中所有元素之和,nN*,求证： 1 2 n    2( 21)  ； a a a 1 2 n m  m3,mN* d(AB)2m1 (3)若A与B都是由 个整数构成的集合,且 ,证明：若按一定顺序排列,集合 A与B中的元素是两个公差相等的等差数列. AB{2,3,4,5,6,7,9,11} 【解析】（1）由题： , 所以1x,3x,5xAB且x1,2,6, 从而1x5,3x7,5x9,故x4. i i A 2j 2j B i  2j i  2j i i j j {1,2, ,n} （2）若 1, 2 n, 1, 2 n,使 1 1 2 2,其中 1, 2, 1, 2  , 2j  j i i j  j i i 则 1 2 2 1,故 1 2, 1 2.   C  i j 2 i, jN*,1i, jn n , a (11 2)(12 2) (1n 2)(2 2)(22 2) (2n 2) (n 2) n    (1n)n n(1n) 1 2 (n2 2) (nn 2)n n 2   n2n3 ,  2 2 2 1 2 n 2  1 1 1   1             2( 21)1 2( 21) a a a 2112 23 n(n1)  n1 . 1 2 n （3）设集合 Aa 1 ,a 2 ,  ,a m  , Bb 1 ,b 2 ,  ,b m  ,其中 a 1 a 2   a m, b 1 b 2   b m. a b a b  a b a b  a b 则 1 1 2 1  m 1 m 2  m m, 2m1 d(AB)2m1 AB 这里共 个不同元素,又 ,所以上面为和集 中的所有元素. a b a b a b  a b a b  a b 又 1 1 1 2 2 2  m 2 m 3  m m, 这里共2m1个不同元素,也为合集AB中的所有元素, a b a b a a b b 所以有 2 1 1 2,即 2 1 2 1. 学科网（北京）股份有限公司a b a b  a b a b  a b a b  a b 1 1 1 2  1 k 2 k  m k m k1  m m 一般地,由 , a b  a b a b a b  a b  a b 1 1  1 k 1 k1 2 k1  m k1  m m , a b a b a a b b 1km1 可得 2 k 1 k1,即 2 1 k1 k . b b a a 1km1 同理可得 2 1 k1 k ,得证. 【例1】（2025届广西“飞天”校际高三上学期7月考试）数列 是正项递增数列,由数列 中所有项 构成集合A,它的任意一个子集记为 ,定义集合B是每一个子集中的所有数之和（即分别写出1个数,2个数, ……n个数之和）. (1)若 ,写出 , 以及集合B； (2) ,将集合B中的元素分成n组,要求每组中最大项与最小项之比不超过2,证明一个符合题意的分组； (3) ,将集合B中的元素分成n组,要求与（2）相同,证明存在这个分组. 【解析】（1） 或 或 , , ； （2）不难发现 共有 个数, 不妨让最大数与最小数之比 , 可以分为[1,2], , ,……, , 假设分为n组,这样最后一个数是第 个, 学科网（北京）股份有限公司只需证明 , 令 ,只需 , , （其中 是 的导数）, 所以 , 所以 ,即不必分至n组即可将 个数全部分完, 在已经分好的组中再多分几组,均可满足题意, 仅 一组中还可再分 组, 显然成立, 故可分至n组,故该分组符合题意； （3）要证 ,其中 ,s是某些数之和, 只需证明 ,假设 ,从而 , 使得 , 所以 , 所以 ,故存在这样的分组. 【例2】（2024届甘肃省兰州第一中学高三下学期测试）信息论之父香农（Shannon）在1948年发表的论 文“通信的数学理论”中指出,任何信息都存在冗余,冗余大小与信息中每个符号（数字、字母或单词）的 出现概率或者说不确定性有关,香农借鉴了热力学的概念,把信息中排除了冗余后的平均信息量称为“信息 熵”,并给出了计算信息熵的数学表达式．设随机变量X所有取值为 ,且 ,定义 的信息熵 (1)当 时,求 的值； 学科网（北京）股份有限公司(2)当 时,若 ,探究 与 的关系,并说明理由； (3)若 ,求此时的信息摘 ． 【解析】（1）若 ,则 ,因此 . （2） 与 正相关,理由如下： 当 时, ,则 , 令 ,则 ,其中 ,所以 则 , 所以函数 在 上单调递增,所以 与 正相关. （3）因为 ,所以 , 故 ,而 , 于是 , 整理得 , 令 ,则 , 两式相减得 , 因此, ,所以 . 【例3】（2024届安徽省芜湖市第一中学高三最后一卷）对于数列 ,如果存在正整数 ,当任意 学科网（北京）股份有限公司正整数 时均有 ,则称 为 的“ 项递增相伴数列”．若 可 取任意的正整数,则称 为 的“无限递增相伴数列”． (1)已知 ,请写出一个数列 的“无限递增相伴数列 ”,并说明理由？ (2)若 满足 ,其中 是首项 的等差数列,当 为 的“无限递增相伴数列” 时,求 的通项公式： (3)已知等差数列 和正整数等比数列 满足： ,其中k是正整数,求 证：存在正整数k,使得 为 的“2024项递增相伴数列”． 【解析】（1）由于 ,我们可以取 ,此时恒有 , 再由 ,当 时, , 所以恒有 ,即 满足题意. （2） 设 , 当 为 的“无限递增相伴数列”时 对任意 恒成立 ,当 时, ,因为 ,所以 ,即 . （3）证明：取 ,若存在这样的正整数k使得 成立, 学科网（北京）股份有限公司所以 , 由 ,得 , 于是 , 又因为 ,所以当 时, , 而 时, , 所以 ,最后说明存在正整数k使得 , 由 , 上式对于充分大的k成立,即总存在满足条件的正整数k a nm 【例4】（2024届福建省泉州第一中学高三下学期适应性测试）已知有穷正项数列 n ,若将每个项 依次围成一圈,满足每一项的平方等于相邻两项平方的乘积,则称该数列可围成一个“HL-Circle”．例如：数  1 1  1,1,1,2,1, , ,1,2 列  2 2 都可围成“HL-Circle”． a a m5 a 1 (1)设 ,当 时,是否存在 使该数列可围成“HL-Circle”,并说明理由： a  (2)若 n 的各项不全相等,且可围成“HL-Circle”． （i）求m的取值集合； a a  a a2a2 a2 maa a ,m7 （ii）求证： 1 2  6 7 8  m 1 2 m ． a2 a2 a2 a  a a a 【解析】（1）由定义可得 i i1 i1,而 n 为正项数列,故 i i1 i1, a aa ,a a a ,a a a ,a aa ,a a a 2 1 3 3 2 4 4 3 5 5 1 4 1 5 2 故 , 学科网（北京）股份有限公司1 a  由最后两式可得 2 a ,故 a 1 ,故 a a a 且 a a , 4 3 1 2 4 5 a a a a 1 a1 a 1 a a a 1 结合 5 4 1可得 1 即 ,故 2 ,故 3 4 5 . a  a  1,1,1,1,1 故存在 a1 ,使得数列 n 可围成“HL-Circle”,此时数列 n 为： . a  （2）（i）若 n 的各项不全相等,且可围成“HL-Circle”． a2 a2 a2 (1nm),a2 a2 a2,a2 a2a2 则由 n n1 n1 m m1 1 1 m 2, a  a a a (1nm),a a a,a a a 结合 n 为正项数列可得 n n1 n1 m m1 1 1 m 2, aa a 1 1 2 m 诸式相乘后可得 , a a a (1nm1) m m n n1 n1 又上述关系式即为 (若下标大于 ,则取下标除以 的余数). a a a (1nm1) n1 n n2 故 , 1 a  (1nm1) 故 n1 a (若下标大于m,则取下标除以m的余数). n2 a a (1nm1) m m n1 n5 所以 (若下标大于 ,则取下标除以 的余数). m6pr,0r5 设 , a aa a aa a 1 a 1 a 1 若 r 1 ,则 m 1 m1即为 1 1 m1,故 m1 ,从而 6 , 3 , a a a a aa a 1 a 1 a a 1 而 1 m 2,故 1 1 2,故 2 ,故 1 ,从而 4 5 , a  a aa a aa a2 a a a a2 此时 n 均为1,与题设矛盾.若 r 2 ,则 m 1 m1即为 2 1 m1 1 ,而 1 2 m 2, a a 1 a a a a 1 a  1 2 ,故 3 4 5 6 ,此时 n 均为1,与题设矛盾. r3 a aa a aa a aa a 1 a 1 若 ,则 m 1 m1即为 3 1 2,而 2 1 3,所以 1 ,故 4 , 学科网（北京）股份有限公司a a a a a a a a a 1 a a 1 3 2 1 2 m 2 3 3 2 5 6 从而 ,而 ,故 ,故 , 此时 a n  均为1,与题设矛盾.若 r 4 ,则 a m a 1 a m1即为 a 4 a 1 a 3,而 a 3 a 2 a 4,所以 a 1 a 2 1 , 1 a a2  而a a a a a ,故 a a ,故 4 1 a ,故 a 1 , 1 2 m 2 4 3 1 1 1 故 a 2 a 3 1 ,故 a 4 1 ,故 a 5 a 6 1 ,此时 a n  均为1,与题设矛盾. 1 a a aa aa a  1 若r =5,则 m 5 1 m1 1 4 1 a ,故a a a a , 1 1 2 m 2 a a a  2 1 a  3 1 故 3 a ,故a a a a 1,故a 1,故 2 a ,故 a 1 , 1 4 5 3 3 6 4 1 a  m6k,kN*,k 2 此时 n 均为1,与题设矛盾.综上, . 1 1 a a a a a a (a  )(a  )( 2  1)6 （ii）由均值不等式得 1 2 3 6 1 a 2 a a a , 1 2 1 2 a a a 1 1 2 3 由上面三组数内必有一组不相等,否则 , a a a 1 a a a a 6 4 5 m 1 2 3 6 从而 与题设矛盾,故等号不成立,从而 , 又m6k,由④和⑥得 1 1 1 (k1) (a2 a2 a2 )6(k1) a2a2 (a2a2)(a2 a2 ) 1 a2 ２ a2 ３ a2 7 m 7 12 6k5 6k 1 ２ ３ 因此由⑤得： a a a a a2a2 66(k1)6k mmaa a a 1 2 3 6 7 m 1 2 3 m． 故原式得证. a  m(m2) 【例5】（2024届重庆市开州中学高三下学期高考模拟）设有穷数列 n 的项数为 ,若正整数 k(2k m) 满足： nk, a n a k,则称 k 为数列 a n  的“ min 点”． 学科网（北京）股份有限公司a (1)n(2n3)(1n5) a  (1)若 n ,求数列 n 的“ min 点”；  1  S   (2)已知有穷等比数列 a n  的公比为 2 ,前 n 项和为S n ．若数列 n S n 存在“ min 点”,求正数a 1 的取值范 围； a a 1(2nm) a  p a a  p (3)若 n n1 ,数列 n 的“ min 点”的个数为 ,证明： 1 m ． a (1)n(2n3)(1n5) a 1,a 1,a 3,a 5,a 7 【解析】（1）因为 n 所以 1 2 3 4 5 , min 所以数列 {a } 的 “ 点” 为 3,5 , n a  12n  1  （2）依题意, S n  1 12 a 1  2n1  ,因为数列   S n  S n  存在 “ min 点”, 1 1 S  a  所以存在 nn2 ,使得 n S 1 a , n 1 所以 a 1  2n1   a 1  2 1 n1  a 1  a 1 1 ,即 a 1  2n2   a 1 1  2 2 n n  1 2 . 1 a2  因为 ,所以 ,所以 , n2 2n20 1 2n1 1 1 又 随 的增大而增大,所以当 时, 取最大值 , 2n1 n n2 2n1 3 1 3 3 1 1 a2  0a  0a  S  S  所以 1 3,又 a 1 0 ,所以 1 3 .当 1 3 时,有 2 S 2 1 S 1 ,  1   3 所以数列   S n  S n   存在 “ min 点”,所以 a 1 的取值范围为    0, 3    , （3）①若 a n a 1 n2 ,则数列{a }不存在 “ min 点”,即 p0 . n a a 0 a a 0 a a  p m 1 1 m 1 m 由 得, ,所以 , a a a ②若存在 n ,使得 n 1 . 下证数列{a }有 “ min 点”. n 学科网（北京）股份有限公司min 证明: 若a