文档内容
2024~2025学年第一学期福建省部分学校教学联盟高中入学适应性检测
高二数学参考答案
一、单项选择题:本题共8小题,每小题5分,共40分。在每小题所给出的四个选项中,只有一个选
项是符合题目要求的。
题号 1 2 3 4 5 6 7 8
答案 C C B D B B C D
二、多项选择题:本题共3小题,每小题6分,共18分。在每小题所给出的四个选项中,有多个选项
是符合题目要求的。全部选对的得6分,部分选对的得部分分,有选错或不选的得0分。
题号 9 10 11
答案 ABD BC ACD
三、填空题:本题共3小题,每小题5分,共15分。
12. 13. 14.
四、解答题:本题共5小题,共77分。解答时应写出文字说明、证明过程或演算步骤。
15.(13分)
解:(1)因为 ,则 ,
可得 ,
则 ,
若 ,则 ,且B∈(0,π),所以 ;
若 ,则 ,即 ,
且 ,所以 ,
但 ,由正弦定理可得 ,不合题意;
综上所述: .
(2)因为 ,则 ,
在 中,由余弦定理可得 ,
1
学科网(北京)股份有限公司即 ,
整理可得 ,解得 或 (舍去),
则 ,所以 的面积 .
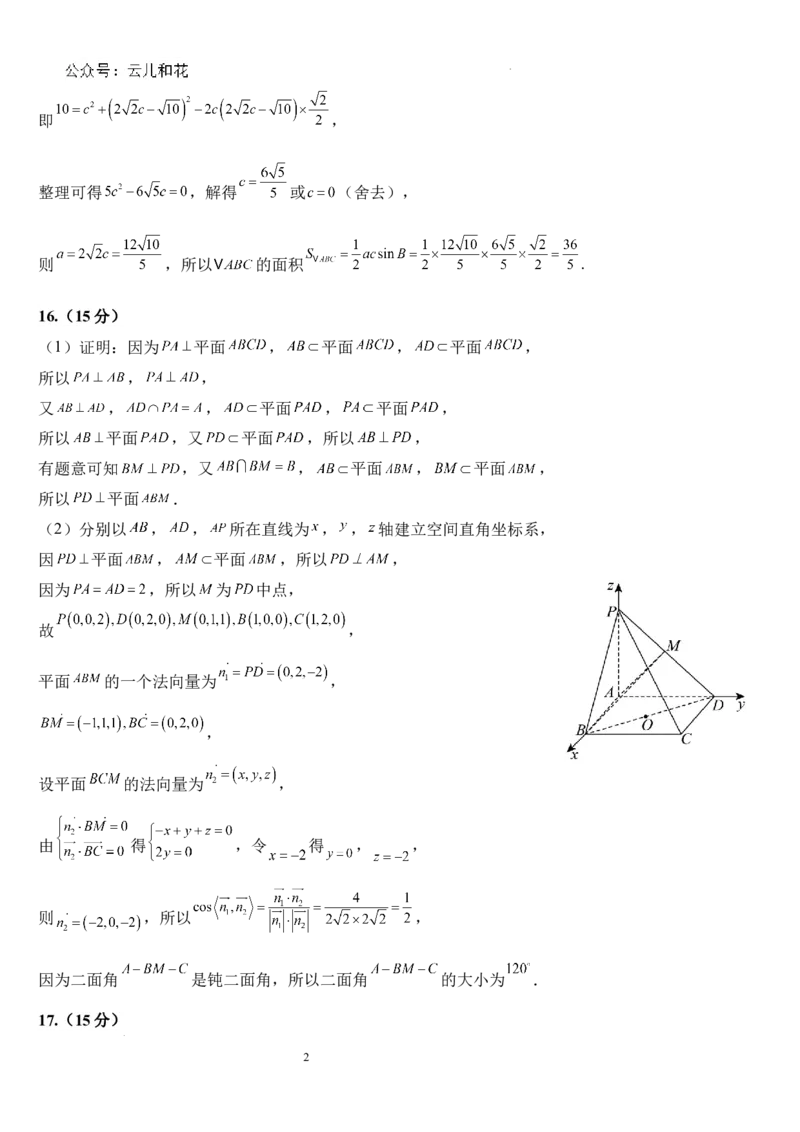
16.(15分)
(1)证明:因为 平面 , 平面 , 平面 ,
所以 , ,
又 , , 平面 , 平面 ,
所以 平面 ,又 平面 ,所以 ,
有题意可知 ,又 , 平面 , 平面 ,
所以 平面 .
(2)分别以 , , 所在直线为 , , 轴建立空间直角坐标系,
因 平面 , 平面 ,所以 ,
因为 ,所以 为 中点,
故 ,
平面 的一个法向量为 ,
,
设平面 的法向量为 ,
由 得 ,令 得 , ,
则 ,所以 ,
因为二面角 是钝二面角,所以二面角 的大小为 .
17.(15分)
2
学科网(北京)股份有限公司(1)证明:三棱台 中, ,则 ,
有 ,得 ,所以 ,
又 ,所以在平面 内, ,有 ,
平面 平面 ,
所以 平面 .
(2)解:已知平面 平面ABC,平面 平面 , ,
平面 ,所以 平面 ,由 平面 ,得 ,
又 平面ABC, 平面ABC,
所以 平面ABC,由 平面ABC,得 .
以B为坐标原点 的方向分别为x轴,y轴,z轴正方向,建立如图空间直角坐标系.
则有 ,
,
因为 ,所以 ,
设向量 ,且满足: ,
则有 ,令 ,
在 的投影数量为 ,
3
学科网(北京)股份有限公司异面直线 与DE的距离 .
18.(17分)
(1)证明:因为E为边AB的中点,所以 .
又 ,即 ,即 .
,
所以 .
又因为 ,所以 ,即 .
因为 平面 ,
所以 平面 .
因为 平面 ,所以 .
(2)解:(i)由余弦定理可得 ,
所以 ,
所以 .
(ii)由(1)可知, 平面 ,
所以 即为 与平面 所成角.
4
学科网(北京)股份有限公司因为 ,所以 , ,
所以 ,得 .
设 到平面 的距离为 ,点 到直线 的距离为 ,
则
.
因为 ,
又 ,所以 .
19.(17分)
解:(1)记平面 , 的法向量为 ,设直线 的方向向量 ,
因为直线 为平面 和平面 的交线,
所以 , ,即 ,取 ,则 ,
所以直线 的单位方向向量为 .
(2)设 ,
由平面 经过点 , ,
所以 ,解得 ,即 ,
所以记平面 的法向量为 ,
5
学科网(北京)股份有限公司与(1)同理, 与 确定的交线方向向量为 ,
所以 ,即 ,解得 .
(3)由集合 知, 由一个边长是4的正方体和6个高为2的正
四棱锥构成,如图所示,
, ,
设几何体 相邻两个面(有公共棱)所成二面角为 ,
平面 ,设平面 法向量 ,
平面 ,设平面 法向量 ,
所以 ,
所以几何体 相邻两个面(有公共棱)所成二面角为 .
6
学科网(北京)股份有限公司