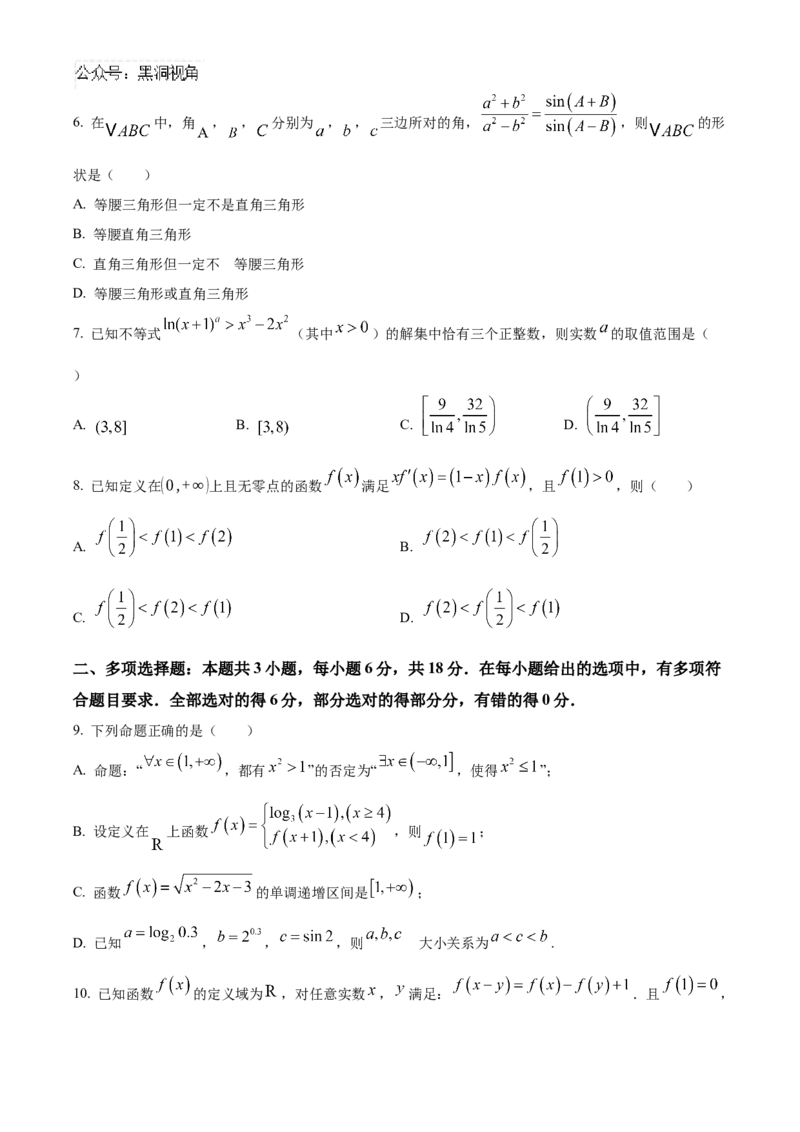文档内容
高三数学自主学习效果评估
2024.10
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有
一项符合题目要求的.
1. 已知角 终边上一点 ,则 ( )
A. B. C. D. 不确定
2. 已知集合 , ,则集合 的真子集个数为( )
A. 7 B. 4 C. 3 D. 2
3. 设a,b都是不等于1的正数,则“ ”是“ ”的( )
A. 充要条件 B. 充分不必要条件
C. 必要不充分条件 D. 既不充分也不必要条件
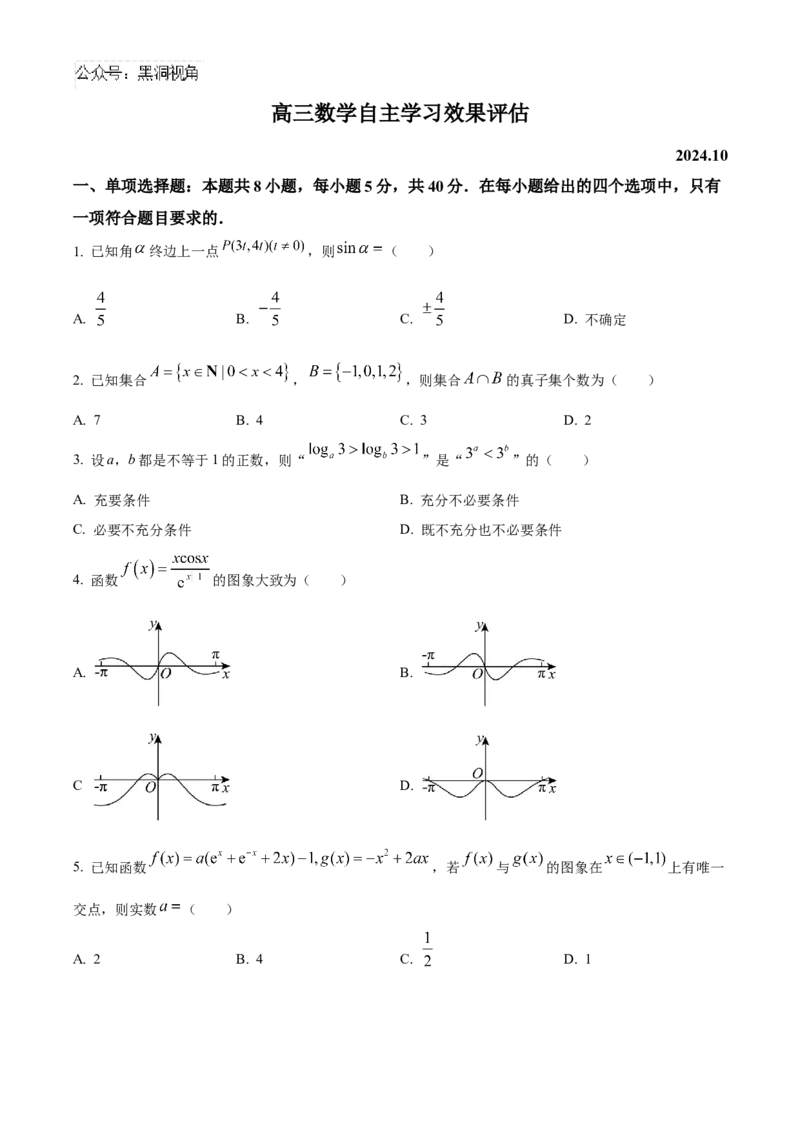
4. 函数 的图象大致为( )
A. B.
C D.
.
5. 已知函数 ,若 与 的图象在 上有唯一
交点,则实数 ( )
A. 2 B. 4 C. D. 16. 在 中,角 , , 分别为 , , 三边所对的角, ,则 的形
状是( )
A. 等腰三角形但一定不是直角三角形
B. 等腰直角三角形
C. 直角三角形但一定不 等是腰三角形
D. 等腰三角形或直角三角形
7. 已知不等式 (其中 )的解集中恰有三个正整数,则实数 的取值范围是(
)
A. B. C. D.
8. 已知定义在(0,+∞)上且无零点的函数 满足 ,且 ,则( )
A. B.
C. D.
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符
合题目要求.全部选对的得6分,部分选对的得部分分,有错的得0分.
9. 下列命题正确的是( )
A. 命题:“ ,都有 ”的否定为“ ,使得 ”;
B. 设定义在 上函数 ,则 ;
C. 函数 的单调递增区间是 ;
的
D. 已知 , , ,则 大小关系为 .
10. 已知函数 的定义域为 ,对任意实数 , 满足: .且 ,当 时, .则下列选项正确的是( )
A. B.
C. 为奇函数 D. 为 上的减函数
11. 已知函数 ,则 ( )
的
A. 函数 最小正周期为
B. 函数 的图象为中心对称图形
C. 函数 在 上单调递增
D. 关于 的方程 在 上至多有3个解
三、填空题:本题共3小题,每小题5分,共15分.
12. _________.
13. 已知幂函数 的图象过点 ,则 的解集为______.
14. 已知 的角 , , 满足 ,其中符号 表示不
大于 的最大整数,若 ,则 ______.
四、解答题:本小题共5小题,计77分.解答应写出必要的文字说明、证明过程或演算步骤.
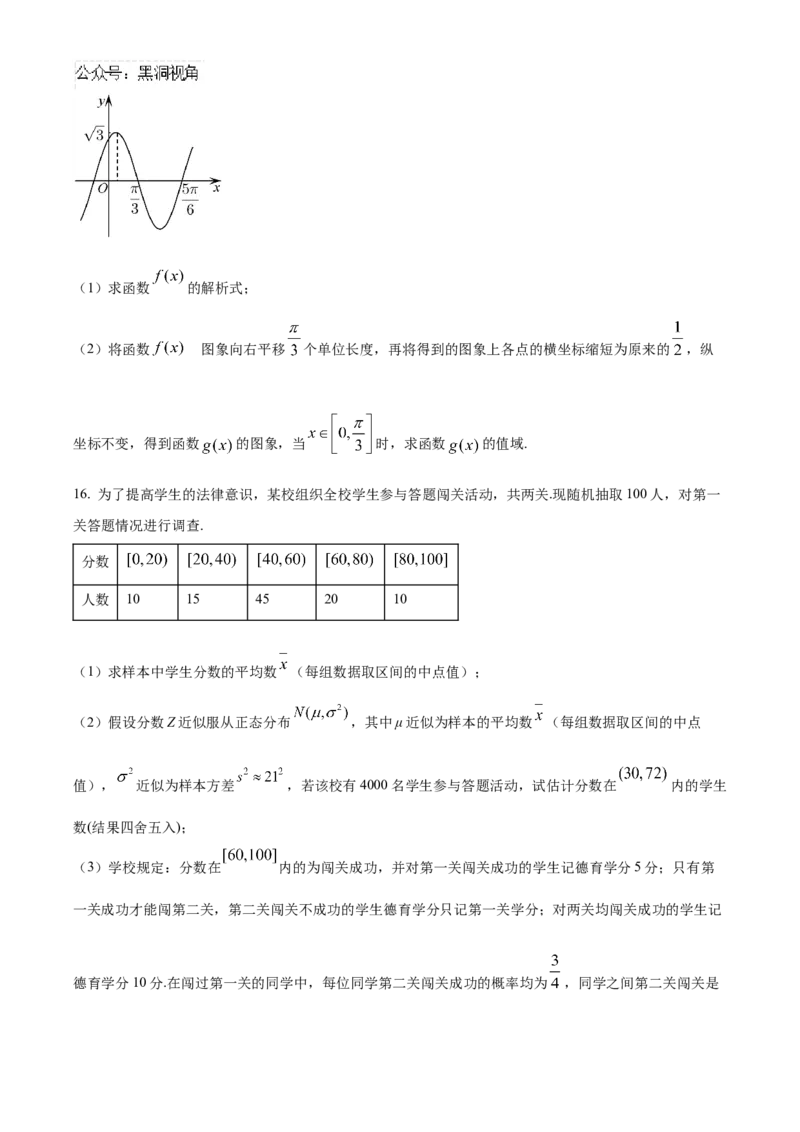
15. 已知函数 的部分图象,如图所示.(1)求函数 的解析式;
(2)将函数 的图象向右平移 个单位长度,再将得到的图象上各点的横坐标缩短为原来的 ,纵
坐标不变,得到函数 的图象,当 时,求函数 的值域.
16. 为了提高学生的法律意识,某校组织全校学生参与答题闯关活动,共两关.现随机抽取100人,对第一
关答题情况进行调查.
分数
人数 10 15 45 20 10
(1)求样本中学生分数的平均数 (每组数据取区间的中点值);
(2)假设分数Z近似服从正态分布 ,其中μ近似为样本的平均数 (每组数据取区间的中点
值), 近似为样本方差 ,若该校有4000名学生参与答题活动,试估计分数在 内的学生
数(结果四舍五入);
(3)学校规定:分数在 内的为闯关成功,并对第一关闯关成功的学生记德育学分5分;只有第
一关成功才能闯第二关,第二关闯关不成功的学生德育学分只记第一关学分;对两关均闯关成功的学生记
德育学分10分.在闯过第一关的同学中,每位同学第二关闯关成功的概率均为 ,同学之间第二关闯关是相互独立的.从第一关闯关成功的学生中随机抽取2人,记2人本次活动总分为随机变量X,求X的分布列
与数学期望.
(参考数据:若随机变量 ,则
)
17. 如图,在四棱锥 中, 为等边三角形, 为 的中点, ,平面
平面 .
(1)证明:平面 平面 ;
(2)若 , , ,直线 与平面 所成角的正弦值为 ,求三棱锥
的体积.
18. 在 中,设角A,B,C所对的边分别是a,b,c,且满足 .
(1)求角B;
(2)若 ,求 面积的最大值;
(3)求 的取值范围.
19. 已知函数 ,其中 .
(1)讨论函数 的单调性;(2)若 ,证明:函数 有唯一的零点;
(3)若 ,求实数a的取值范围.高三数学自主学习效果评估
2024.10
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有
一项符合题目要求的.
【1题答案】
【答案】C
【2题答案】
【答案】C
【3题答案】
【答案】B
【4题答案】
【答案】A
【5题答案】
【答案】C
【6题答案】
【答案】C
【7题答案】
【答案】D
【8题答案】
【答案】D
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符
合题目要求.全部选对的得6分,部分选对的得部分分,有错的得0分.
【9题答案】
【答案】BD
【10题答案】
【答案】ACD
【11题答案】
【答案】AC
三、填空题:本题共3小题,每小题5分,共15分.
【12题答案】【答案】 ##
【13题答案】
【答案】
【14题答案】
【答案】5
四、解答题:本小题共5小题,计77分.解答应写出必要的文字说明、证明过程或演算步骤.
【15题答案】
【答案】(1)
(2)
【16题答案】
【答案】(1)
(2)2730人 (3)
【17题答案】
【答案】(1)证明见解析;
(2) 或
【18题答案】
【答案】(1)
(2)
(3)【19题答案】
【答案】(1)答案见解析
(2)证明见解析 (3)