文档内容
2024 学年第一学期初三年级 10 月学情摸查数学试卷
第一部分 选择题(共30分)
一、选择题(本大题共10小题,每小题3分,满分30分)
1.下列四个2024年巴黎奥运会项目图标中,不是中心对称图形的是( )
A. B. C. D.
2.在平面直角坐标系中,点P1,2关于原点对称的点的坐标是( )
A.(1,-2) B.(-1,2) C.(1,2) D.(-2,-1)
3.下列关于二次函数y 3x2 1的图象说法中,错误的是( )
A.它的对称轴是直线x0 B.它的图象有最低点
C.它的顶点坐标是(0,-1) D.在对称轴的左侧,y随着x的增大而增大
15
4.用配方法解方程x2 x 0时,变形结果正确的是( )
4
2 2
1 1 7
A. x 4 B. x
2 2 2
2 2
1 1 7
C. x 4 D. x
4 4 2
5.已知一元二次方程x2 x20的一个根为m,则2023m2 m的值是( )
A.2020 B.2021 C.2023 D.2025
6.已知抛物线y x2 2x1,则当0 x3时,函数的最大值为( )
A.-2 B.-1 C.0 D.2
7.在如图所示的正方形网格中,四边形ABCD绕某一点旋转某一角度得到四形ABCD(所有顶点都是网
格线交点),在网格线交点M,N,P,Q中,可能是旋转中心的是( )
A.点M B.点N C.点P D.点Q
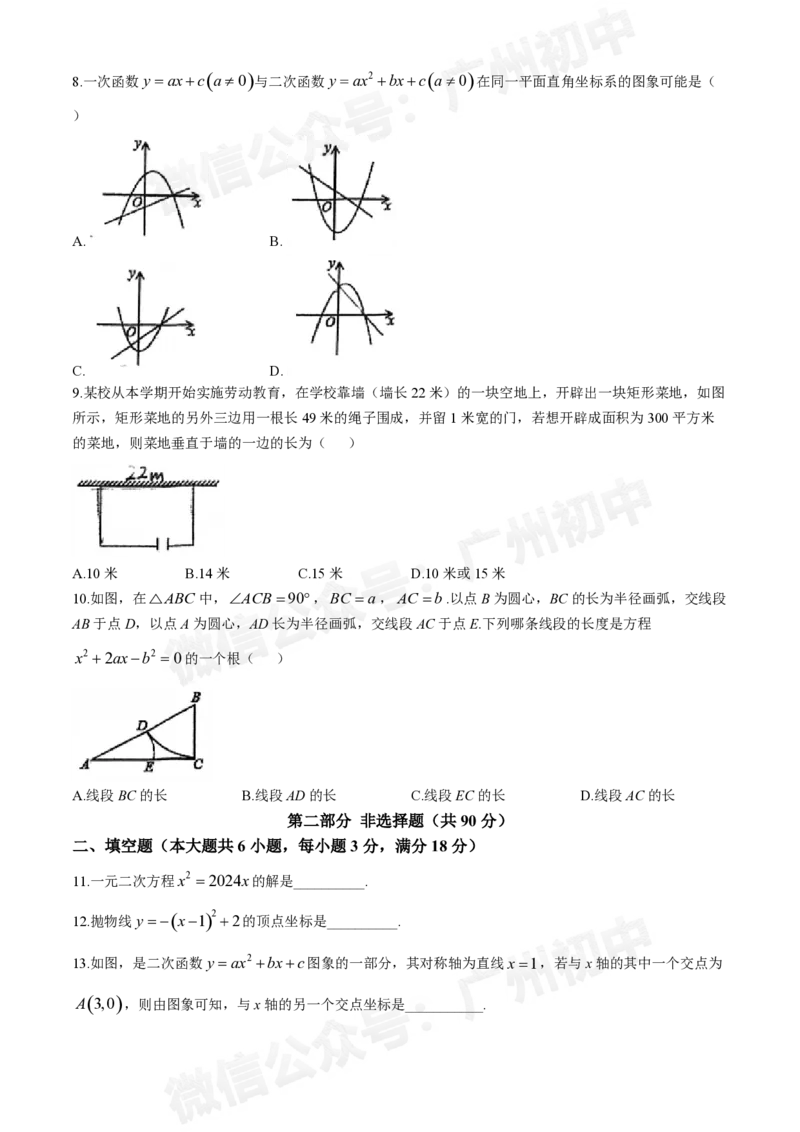
学科网(北京)股份有限公司8.一次函数y axca 0与二次函数y ax2 bxca0在同一平面直角坐标系的图象可能是(
)
A. B.
C. D.
9.某校从本学期开始实施劳动教育,在学校靠墙(墙长22米)的一块空地上,开辟出一块矩形菜地,如图
所示,矩形菜地的另外三边用一根长49米的绳子围成,并留1米宽的门,若想开辟成面积为300平方米
的菜地,则菜地垂直于墙的一边的长为( )
A.10米 B.14米 C.15米 D.10米或15米
10.如图,在△ABC中,ACB90,BC a,AC b.以点B为圆心,BC的长为半径画弧,交线段
AB于点D,以点A为圆心,AD长为半径画弧,交线段AC于点E.下列哪条线段的长度是方程
x2 2axb2 0的一个根( )
A.线段BC的长 B.线段AD的长 C.线段EC的长 D.线段AC的长
第二部分 非选择题(共90分)
二、填空题(本大题共6小题,每小题3分,满分18分)
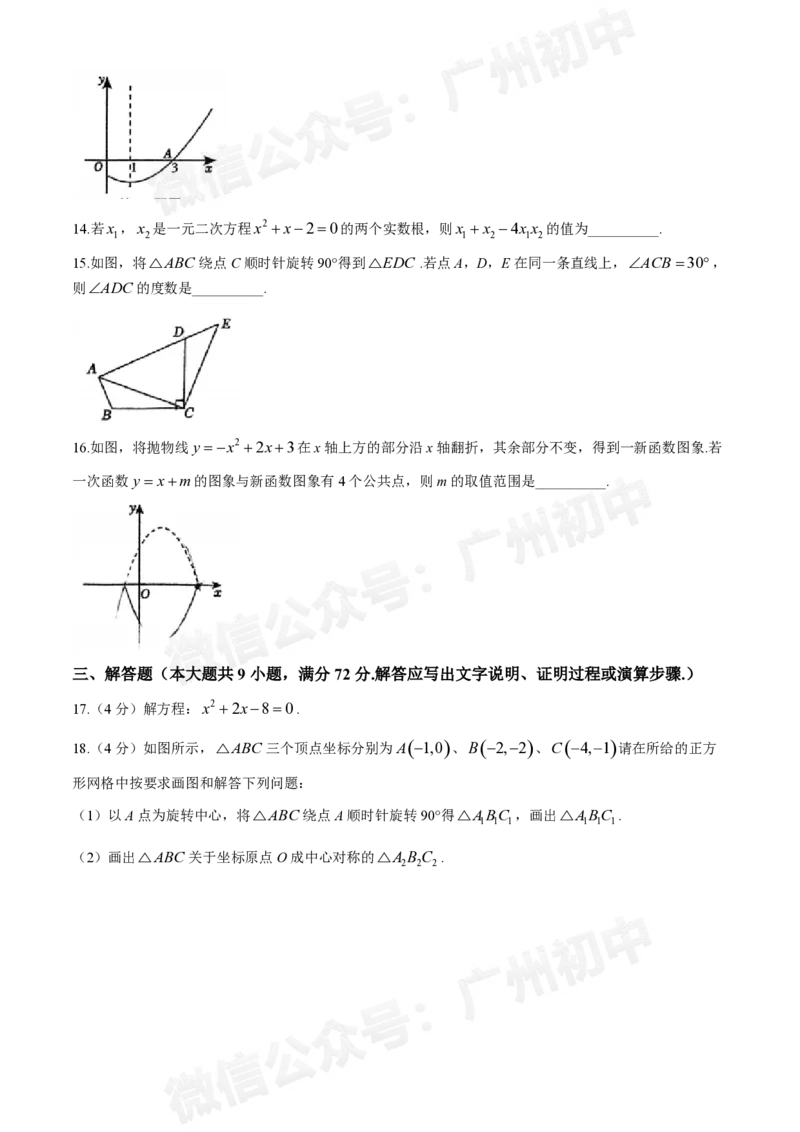
11.一元二次方程x2 2024x的解是__________.
12.抛物线y
x12
2的顶点坐标是__________.
13.如图,是二次函数y ax2 bxc图象的一部分,其对称轴为直线x1,若与x轴的其中一个交点为
A3,0,则由图象可知,与x轴的另一个交点坐标是___________.
学科网(北京)股份有限公司14.若x ,x 是一元二次方程x2 x20的两个实数根,则x x 4x x 的值为__________.
1 2 1 2 1 2
15.如图,将△ABC绕点C顺时针旋转90°得到△EDC .若点A,D,E在同一条直线上,ACB30,
则ADC的度数是__________.
16.如图,将抛物线y x2 2x3在x轴上方的部分沿x轴翻折,其余部分不变,得到一新函数图象.若
一次函数y xm的图象与新函数图象有4个公共点,则m的取值范围是__________.
三、解答题(本大题共9小题,满分72分.解答应写出文字说明、证明过程或演算步骤.)
17.(4分)解方程:x2 2x80.
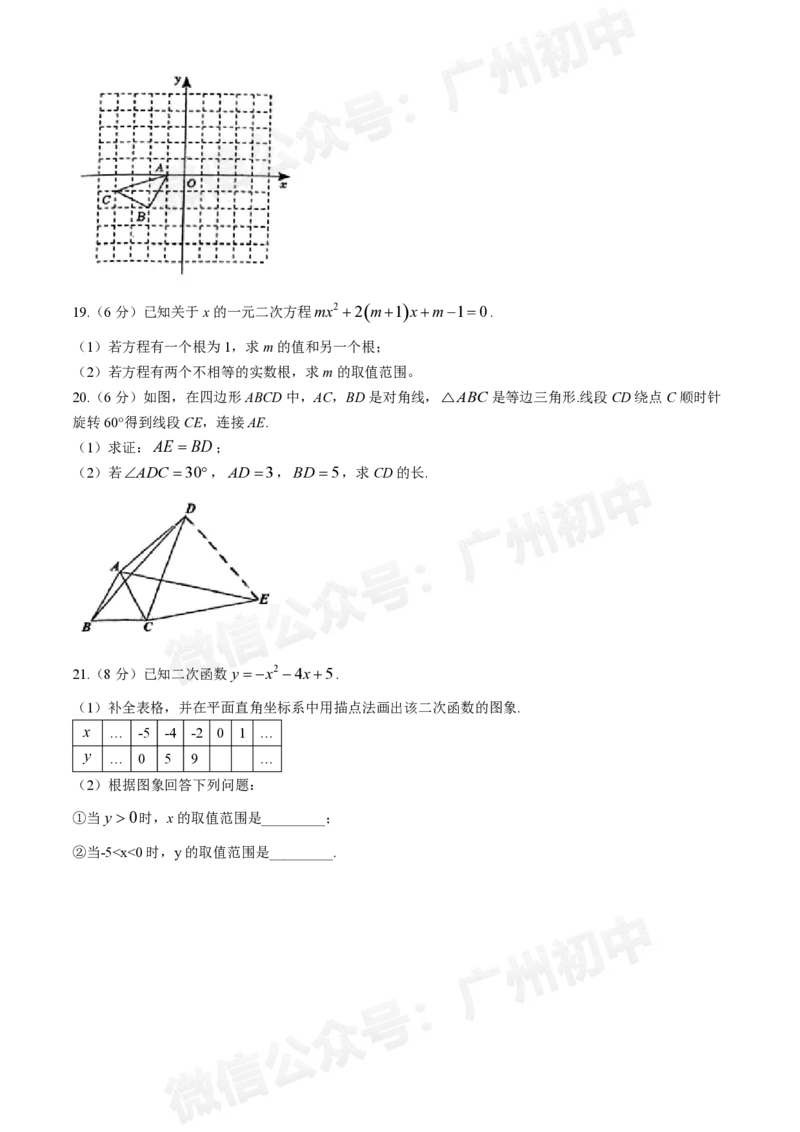
18.(4分)如图所示,△ABC三个顶点坐标分别为A1,0、B2,2、C4,1请在所给的正方
形网格中按要求画图和解答下列问题:
(1)以A点为旋转中心,将△ABC绕点A顺时针旋转90°得△ABC ,画出△ABC .
1 1 1 1 1 1
(2)画出△ABC关于坐标原点O成中心对称的△A B C .
2 2 2
学科网(北京)股份有限公司19.(6分)已知关于x的一元二次方程mx2 2m1xm10.
(1)若方程有一个根为1,求m的值和另一个根;
(2)若方程有两个不相等的实数根,求m的取值范围。
20.(6分)如图,在四边形ABCD中,AC,BD是对角线,△ABC是等边三角形.线段CD绕点C顺时针
旋转60°得到线段CE,连接AE.
(1)求证:AE BD;
(2)若ADC 30,AD3,BD5,求CD的长.
21.(8分)已知二次函数y x2 4x5.
(1)补全表格,并在平面直角坐标系中用描点法画出该二次函数的图象.
x … -5 -4 -2 0 1 …
y
… 0 5 9 …
(2)根据图象回答下列问题:
①当y 0时,x的取值范围是_________;
②当-5