铁一中学2024-2025学年九年级10月月考数学试题答案解析_广州九上月考+期中+期末+一模二模+中考真题_九上月考_初三上十月考

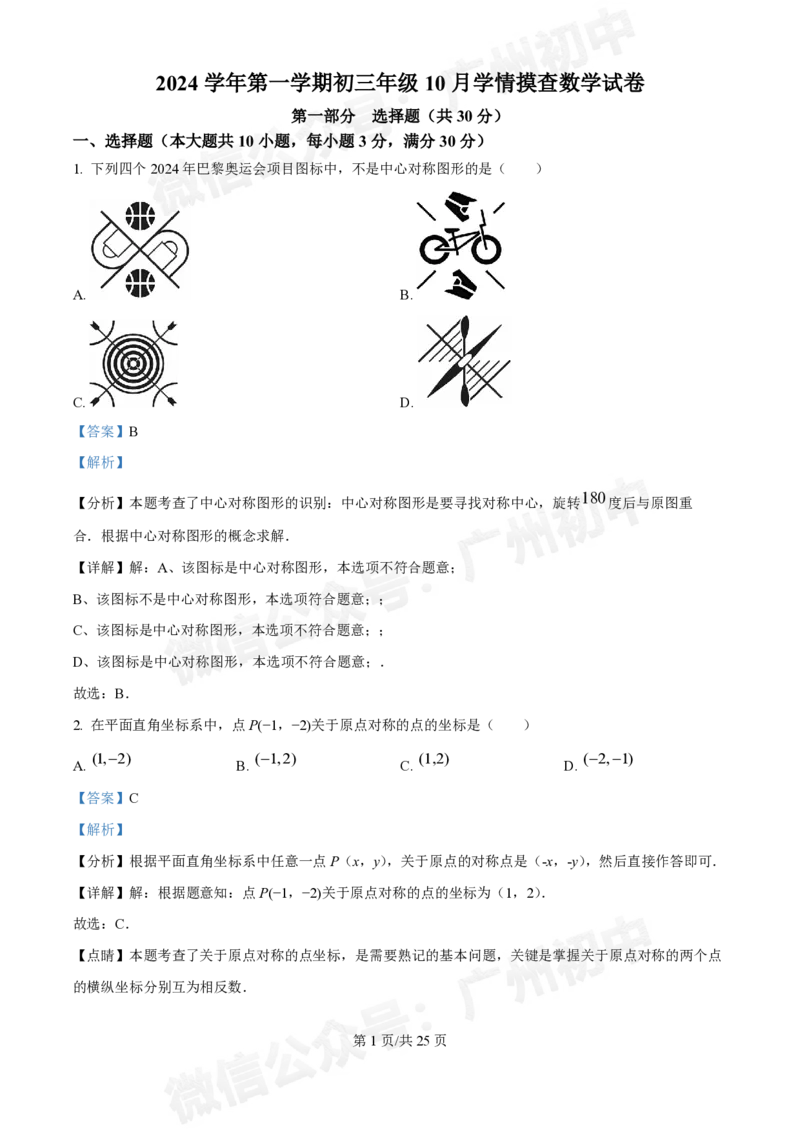
2024 学年第一学期初三年级 10 月学情摸查数学试卷 第一部分 选择题（共30分） 一、选择题（本大题共10小题，每小题3分，满分30分） 1. 下列四个2024年巴黎奥运会项目图标中，不是中心对称图形的是（ ） A. B. C. D. 【答案】B 【解析】 180 【分析】本题考查了中心对称图形的识别：中心对称图形是要寻找对称中心，旋转 度后与原图重 合．根据中心对称图形的概念求解． 【详解】解：A、该图标是中心对称图形，本选项不符合题意； B、该图标不是中心对称图形，本选项符合题意；； C、该图标是中心对称图形，本选项不符合题意；； D、该图标是中心对称图形，本选项不符合题意；． 故选：B． 2. 在平面直角坐标系中，点P(−1，−2)关于原点对称的点的坐标是（ ） (1,2) (1,2) (1,2) (2,1) A. B. C. D. 【答案】C 【解析】 【分析】根据平面直角坐标系中任意一点P（x，y），关于原点的对称点是（-x，-y），然后直接作答即可． 【详解】解：根据题意知：点P(−1，−2)关于原点对称的点的坐标为（1，2）． 故选：C． 【点睛】本题考查了关于原点对称的点坐标，是需要熟记的基本问题，关键是掌握关于原点对称的两个点 的横纵坐标分别互为相反数． 第1页/共25页 学科网（北京）股份有限公司y 3x2 1 3. 下列关于二次函数 的图象说法中，错误的是（ ） x0 A. 它的对称轴是直线 B. 它的图象有最低点 0,1 C. 它的顶点坐标是 D. 在对称轴的左侧，y随着x的增大而增大 【答案】D 【解析】 x0 【分析】本题主要考查了二次函数的性质，根据解析式可知，函数开口向上，对称轴为直线 ，顶点 0,1 坐标为 ，则函数有最小值，在对称轴左侧y随着x的增大而减小，据此可得答案． x0 【详解】解：A、它的对称轴是直线 ，原说法正确，不符合题意； B、由二次项系数大于0可知，函数开口向上，则它的图象有最低点，原说法正确，不符合题意； 0,1 C、它的顶点坐标是 ，原说法正确，不符合题意； D、函数开口向上，在对称轴的左侧，y随着x的增大而减小，原说法错误，符合题意； 故选：D． 15 x2 x 0 4 4. 用配方法解方程 时，变形结果正确的是（ ） 2 2 2 2  1  1 7  1  1 7 x 4 x  x 4 x           2  2 2  4  4 2 A. B. C. D. 【答案】A 【解析】 【分析】本题考查了配方法解一元二次方程，掌握配方法的步骤是解题的关键．根据配方法的步骤先把常 数项移到等号的右边，再在等式两边同时加上一次项系数一半的平方，配成完全平方的形式，从而得出答 案． 15 x2 x 0 4 【详解】解：∵ ， 15 x2 x 4 ∴ ， 第2页/共25页 学科网（北京）股份有限公司1 15 1 x2 x   ∴ 4 4 4， 2  1 x 4    2 ∴ ； 故选：A． 5. 已知一元二次方程 x2 x20 的一个根是 m ，则2023m2 m的值是（ ） 2020 2021 2023 2025 A. B. C. D. 【答案】B 【解析】 【分析】此题考查了一元二次方程的解，把xm代入方程求出 m2 m20 ，然后利用整体代入求值 即可，解题的关键是熟记把方程的解代入原方程，等式左右两边相等． 【详解】解：将xm代入原方程得： m2 m20 ， m2 m 2 ∴ ， 2023m2 m2023  m2 m  202322021 则 ， 故选：B． y  x2 2x1 0 x3 6. 已知抛物线 ，则当 时，函数的最大值为（ ） A. 2 B. 1 C. 0 D. 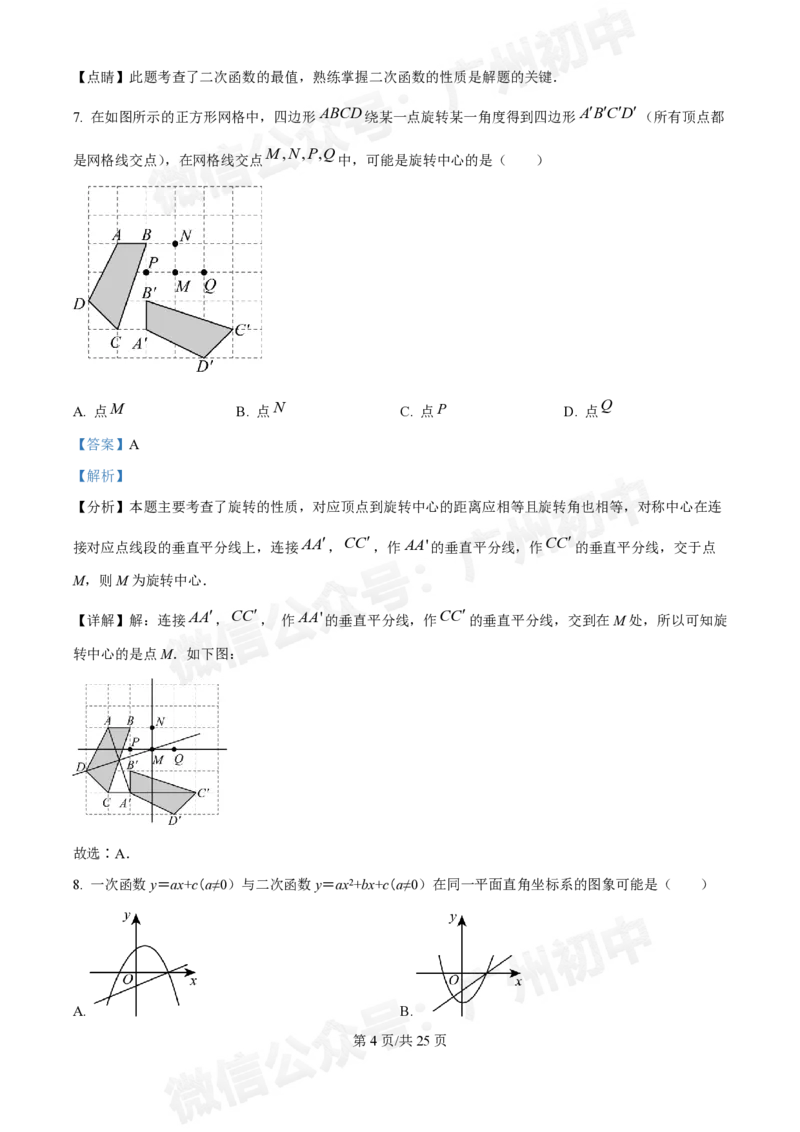2 【答案】D 【解析】 y  x2 2x1 【分析】把抛物线 化为顶点式，得到对称轴为 x1 ，当 x1 时，函数的最小值为2， x0 x3 再分别求出 和 时的函数值，即可得到答案． y  x2 2x1x12 2 【详解】解：∵ ， ∴对称轴为 x1 ，当 x1 时，函数的最小值为2， x0 y  x2 2x11 x3 y 32 2312 当 时， ，当 时， ， 0 x3 ∴当 时，函数的最大值为2， 故选：D 第3页/共25页 学科网（北京）股份有限公司【点睛】此题考查了二次函数的最值，熟练掌握二次函数的性质是解题的关键． ABCD ABCD 7. 在如图所示的正方形网格中，四边形 绕某一点旋转某一角度得到四边形 （所有顶点都 M,N,P,Q 是网格线交点），在网格线交点 中，可能是旋转中心的是（ ） A. 点M B. 点 N C. 点P D. 点 Q 【答案】A 【解析】 【分析】本题主要考查了旋转的性质，对应顶点到旋转中心的距离应相等且旋转角也相等，对称中心在连 接对应点线段的垂直平分线上，连接AA ， CC ，作AA'的垂直平分线，作 CC 的垂直平分线，交于点 M，则M为旋转中心． 【详解】解：连接AA ， CC ， 作AA'的垂直平分线，作 CC 的垂直平分线，交到在M处，所以可知旋 转中心的是点M．如下图： 故选∶A． 8. 一次函数y＝ax+c（a≠0）与二次函数y＝ax2+bx+c（a≠0）在同一平面直角坐标系的图象可能是（ ） A. B. 第4页/共25页 学科网（北京）股份有限公司C. D. 【答案】D 【解析】 【分析】根据直线和抛物线解析式知y＝ax+c与y＝ax2+bx+c与y轴交于同一点（0，c），据此可得． 【详解】在y＝ax+c中，当x＝0时，y＝c，∴y＝ax+c与y轴的交点为（0，c）； 在y＝ax2+bx+c中，当x＝0时，y＝c，∴y＝ax2+bx+c与y轴的交点为（0，c），则y＝ax+c与y＝ax2+bx+c与 y轴交于同一点（0，c）． 故选D． 【点睛】本题考查了二次函数的图象和一次函数的图象，解题的关键是明确一次函数和二次函数的性质． 9. 某校从本学期开始实施劳动教育，在学校靠墙（墙长22米）的一块空地上，开辟出一块矩形菜地，如 300 图所示，矩形菜地的另外三边用一根长49米的绳子围成，并留1米宽的门，若想开辟成面积为 平方 米的菜地，则菜地垂直于墙的一边的长为（ ） A. 10米 B. 14米 C. 15米 D. 10米或15米 【答案】C 【解析】 【分析】本题考查的是一元二次方程的应用，找准等量关系列出方程是解题的关键． 根据题意，设菜地垂直于墙的一边的长为x米，则根据图形并利用长宽和面积，建立方程并求解即可． 4912x 【详解】解：设菜地垂直于墙的一边的长为x米，则平行于墙的一边的长为 米， x4912x300 由题意得： ， x 10 x 15 解得 1 ， 2 ， 4912x30 当菜地垂直于墙的一边的长为10米时，平行于墙的一边的长为 米，大于墙长的22米， x 10 ∴ 1 不合题意，舍去， 第5页/共25页 学科网（北京）股份有限公司∴菜地垂直于墙的一边的长为15米． 故选：C． 10. 如图，在△ABC中，∠ACB＝90°，BC＝a，AC＝b．以点B为圆心，BC的长为半径画弧，交线段AB 于点D，以点A为圆心，AD长为半径画弧，交线段AC于点E．下列哪条线段的长度是方程 x2+2ax－b2＝0的一个根（ ） 的 A. 线段AD 长 B. 线段BC的长 C. 线段EC的长 D. 线段AC的长 【答案】A 【解析】 x2 2axb2 0 【分析】由方程 的解结合线段的和差可以得到答案． Qx2 2axb2 0, 【详解】解： (2a)2 41(b2)4a2 4b2 ， 2a 4a2 4b2 x 2 ， Q ∠ACB＝90°，BC＝a，AC＝b， a2 b2  AB2, 2a2AB x a AB, 2 x a AB,x aAB, 1 2 Q ABa  ABBC  ABBD AD, 线段AD的长是 x2 2axb2 0 的根， 故选：A． 【点睛】本题考查一元二次方程的解法，掌握公式法解一元二次方程是解题关键． 第二部分 非选择题（共90分） 二、填空题（本大题共6小题，每小题3分，满分18分） x2 2024x 11. 一元二次方程 的解是________． 第6页/共25页 学科网（北京）股份有限公司x 0，x 2024 【答案】 1 2 【解析】 【分析】本题主要考查了解一元二次方程．熟练掌握因式分解法解一元二次方程，是解决问题的关键． 移项，提公因式x，化成两个一元一次方程解答即可． x2 2024x 【详解】∵ ， x2 2024x0 ∴移项得， ， xx20240 分解因式得， ， ∴x0，x20240， x 0，x 2024 ∴ 1 2 ． x 0，x 2024 故答案为： 1 2 ． y (x1)2 2 12. 抛物线 的顶点坐标是__________． (1,2) 【答案】 【解析】 【分析】直接利用顶点式的特点可求顶点坐标． Q y(x1)2 2 【详解】解： 是抛物线的顶点式， (1,2) 顶点坐标为 ． (1,2) 故答案为： ． 【点睛】此题考查二次函数的性质，掌握顶点式得性质是解决问题的关键． y ax2 bxc x1 x 13. 如图，是二次函数 图象的一部分，其对称轴为直线 ，若与 轴的其中一个交点 A(3,0) x 为 ，则由图象可知，与 轴的另一个交点坐标是______． 第7页/共25页 学科网（北京）股份有限公司(1,0) 【答案】 【解析】 x 【分析】本题主要考查的是抛物线与 轴的交点，利用抛物线的对称性求解是解题的关键．利用抛物线的 x 对称性即可求得抛物线与 轴的另一个交点坐标． 【详解】解：Q点 (1,0) 与 (3,0) 关于直线 x1 对称， 抛物线与 x 轴的另一个交点坐标为 (1,0) ． (1,0) 故答案为： ． x x x2 x20 x x 4x x 14. 若 1， 2是一元二次方程 的两个实数根，则 1 2 1 2的值为 _____________． 【答案】7 【解析】 【分析】本题考查了一元二次方程根与系数的关系，正确理解一元二次方程根与系数的关系是解题的关 x x 1 x x  2 x x 4x x 键．根据一元二次方程根与系数的关系，得到 1 2 ， 1 2 ，再代入 1 2 1 2即得答 案． x x 1 x x  2 【详解】根据题意，得 1 2 ， 1 2 ， x x 4xx 14(2)187 1 2 1 2 ． 故答案为：7． 15. 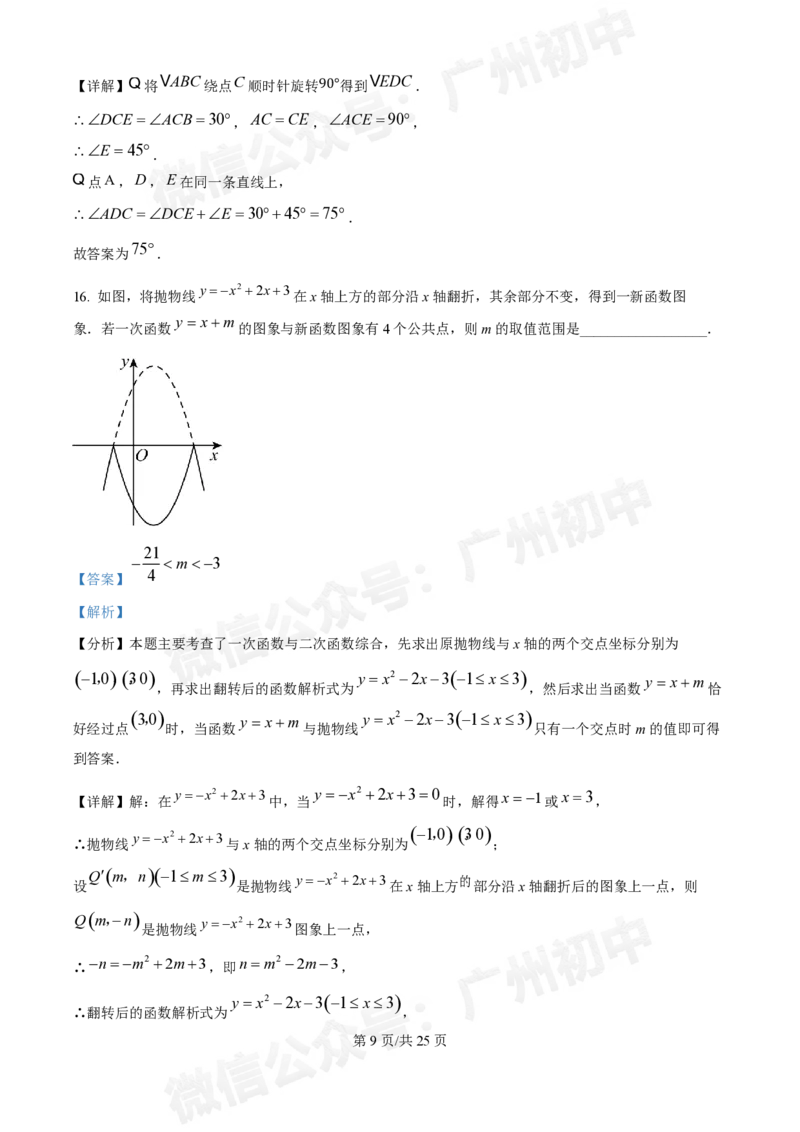如图，将 VABC绕点C顺时针旋转90°得到 △EDC ．若点A，D，E在同一条直线上， ACB30 ，则ADC 的度数是__________． 75 75 【答案】 ## 度 【解析】 【分析】本题主要考查了旋转的性质，等腰三角形的性质与判定，根据旋转的性质求出E和 DCE 度 ADC DCEE 数，利用三角形外角的性质 即可． 第8页/共25页 学科网（北京）股份有限公司【详解】Q将 VABC 绕点C顺时针旋转90°得到 VEDC ． DCE ACB30 AC CE ACE 90 ， ， ， E 45 ． Q点A，D，E在同一条直线上， ADC DCEE 304575 ． 75 故答案为 ． yx2 2x3 16. 如图，将抛物线 在x轴上方的部分沿x轴翻折，其余部分不变，得到一新函数图 y  xm 象．若一次函数 的图象与新函数图象有4个公共点，则m的取值范围是__________________． 21  m3 【答案】 4 【解析】 【分析】本题主要考查了一次函数与二次函数综合，先求出原抛物线与x轴的两个交点坐标分别为 1，0，，30 y  x2 2x31 x3 y  xm ，再求出翻转后的函数解析式为 ，然后求出当函数 恰 3，0 y  xm y  x2 2x31 x3 好经过点 时，当函数 与抛物线 只有一个交点时m的值即可得 到答案． 【详解】解：在 yx2 2x3 中，当 y x2 2x30 时，解得x1或 x3 ， yx2 2x3 1，0，，30 ∴抛物线 与x轴的两个交点坐标分别为 ； Qm，n1m3 yx2 2x3 的 设 是抛物线 在x轴上方 部分沿x轴翻折后的图象上一点，则 Qm，n yx2 2x3 是抛物线 图象上一点， nm2 2m3 nm2 2m3 ∴ ，即 ， y  x2 2x31 x3 ∴翻转后的函数解析式为 ， 第9页/共25页 学科网（北京）股份有限公司当函数 y  xm 恰好经过点 3，0 时，则03m，解得 m3 ， y  xm y  x2 2x31 x3 当函数 与抛物线 只有一个交点时， y  xm  y  x2 2x3 x2 3x3m0 联立 得 ， 21 Δ32 43m0 m 4 当 时， ， 21  m3 ∴由函数图象可知，当 4 时，一次函数 y  xm 的图象与新函数图象有4个公共点， 21  m3 故答案为： 4 ． 三、解答题（本大题共9小题，满分72分．解答应写出文字说明、证明过程或演算步骤．） x2 2x80 17. 解方程： ． x 4，x 2 【答案】 1 2 【解析】 【分析】本题主要考查了解一元二次方程，把方程左边利用十字相乘法进行因式分解，然后解方程即可． x2 2x80 【详解】解：∵ ， x4x20 ∴ ， ∴x40或 x20 ， x 4，x 2 解得 1 2 ． A1,0 B2,2 C4,1 18. 如图所示， VABC三个顶点坐标分别为 、 、 请在所给的正方形网格中 按要求画图和解答下列问题： 第10页/共25页 学科网（北京）股份有限公司（1）以A点为旋转中心，将 VABC绕点A顺时针旋转90°得 △A 1 B 1 C 1，画出 △A 1 B 1 C 1． （2）画出 VABC关于坐标原点 O 成中心对称 的△A 2 B 2 C 2． 【答案】（1）见解析 （2）见解析 【解析】 【分析】本题主要考查了坐标与图形变化—旋转和中心对称： 90 （1）分别作出点B、C绕点A顺时针旋转 得到的对应点，再与点A首尾顺次连接即可； （2）分别作出三个顶点关于原点的对称点，再首尾顺次连接即可． 【小问1详解】 △ABC 解：如图所示， 1 1 1即为所求； 【小问2详解】 △ABC 解：如图所示， 2 2 2即为所求； 第11页/共25页 学科网（北京）股份有限公司mx2 2m1xm10 19. 已知关于x的一元二次方程 ． （1）若方程有一个根为1，求m的值和另一个根； （2）若方程有两个不相等的实数根，求m的取值范围． 1 m 【答案】（1） 4 ， x5 ； 1 m （2） 3且 m0 ． 【解析】 【分析】本题考查了一元二次方程根的判别式，一元二次方程定义和解，根与系数关系等知识．熟知一元 ax2bxc0(a0) b2 4ac  0 二次方程 的根与 有如下关系：当 时，方程有两个不相等的两个实  0 0 数根；当 时，方程有两个相等的两个实数根；当 时，方程无实数根是解题的关键． x1 （1）由于 是方程的一个根，直接把它代入方程即可求出m的值，再根据根与系数关系求出方程的另 一个根即可； m0  0 （2）根据方程定义得到 ，根据根的判别式公式，令 ，得到关于m的一元一次不等式，解之 即可． 【小问1详解】 mx2 2m1xm10 m2m1m10 x1 解：把 代入 得： ， 第12页/共25页 学科网（北京）股份有限公司1 m 4 ； 1 3 5  x2  x 0 4 2 4 x2 6x50 ∴方程为 ，即 ， x x 16 设方程的另一个根为 1，则 1 ， x 5 ∴ 1 ， x5 即方程另一个根为 ； 【小问2详解】 m0 解：根据一元二次方程定义得到， ， 又Q方程有两个不相等的实数根， Δ4m12 4mm10  ， 即4(𝑚+1)2‒4𝑚(𝑚‒1)>0， 12m40 则 1 m ∴ 3． 1 m ∴m的取值范围为 3且 m0 ． 20. 如图，在四边形 ABCD 中， AC ，BD是对角线， VABC是等边三角形．线段 CD 绕点C顺时针旋 转 60 得到线段 CE ，连接AE． （1）求证：AE  BD； （2）若ADC30， AD3 ， BD5 ，求 CD 的长． 【答案】（1）见解析 （2）4 【解析】 第13页/共25页 学科网（北京）股份有限公司【分析】(1)证明 VACE≌VBCD即可． (2)连接DE，证明 △DCE 是等边三角形，得到 ADC 90 ，利用勾股定理计算即可． 【小问1详解】 ∵ VABC是等边三角形， AC  BC,BCA60 ∴ ； CD 60 CE ∵线段 绕点C顺时针旋转 得到线段 ， CE CD,DCE 60 ∴ ； ∴BCAACDDCEACD； BCDACE ∴ ； BC  AC  BCDACE  CDCE  ∵ ， VACE≌VBCDSAS ∴ ∴AE  BD． 【小问2详解】 连接DE， CD 60 CE ∵线段 绕点C顺时针旋转 得到线段 ， CE CD,DCE 60 ∴ ； △DCE ∴ 是等边三角形， DE CD,CDE 60 ∴ ； ∵ADC30， AD3 ， BD5 ， AE  BD5,ADC 90 ∴ ； 第14页/共25页 学科网（北京）股份有限公司DE  AE2 AD2 4 ∴ ； CD4 ∴ ． 【点睛】本题考查了等边三角形的判定和性质，三角形全等的判定和性质，旋转的性质，勾股定理，熟练 掌握等边三角形的判定和性质，勾股定理是解题的关键． y x2 4x5 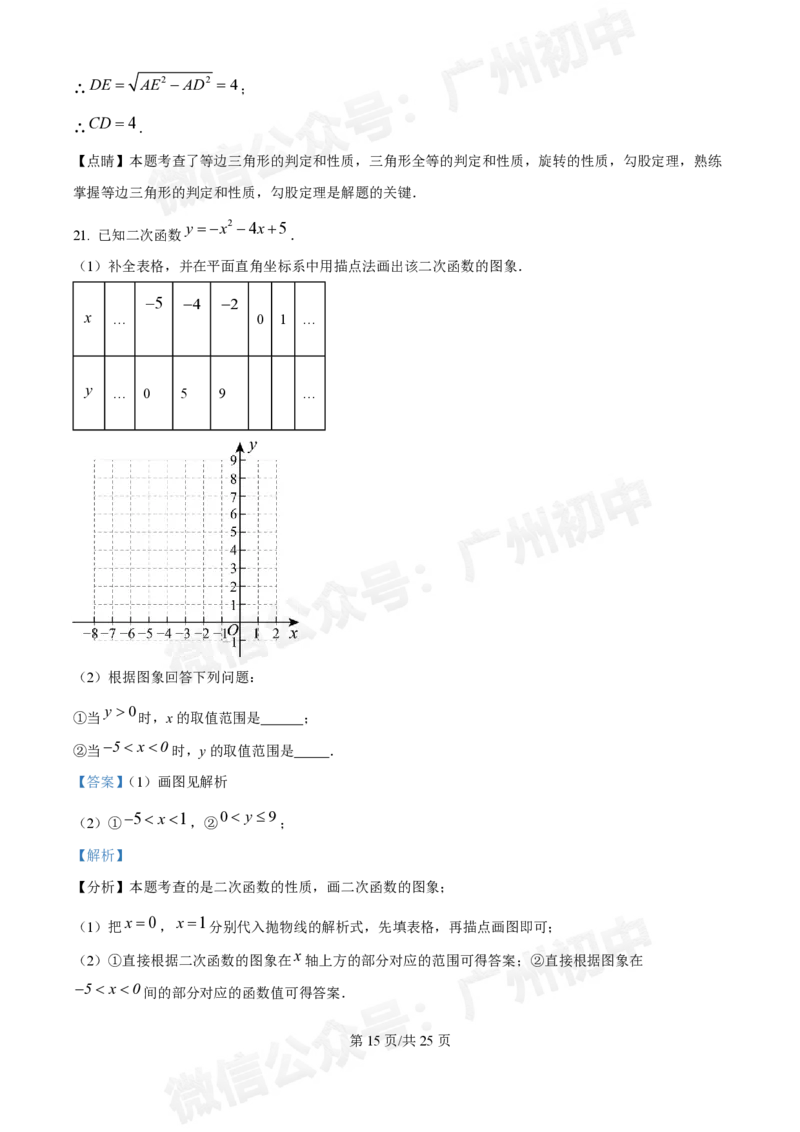21. 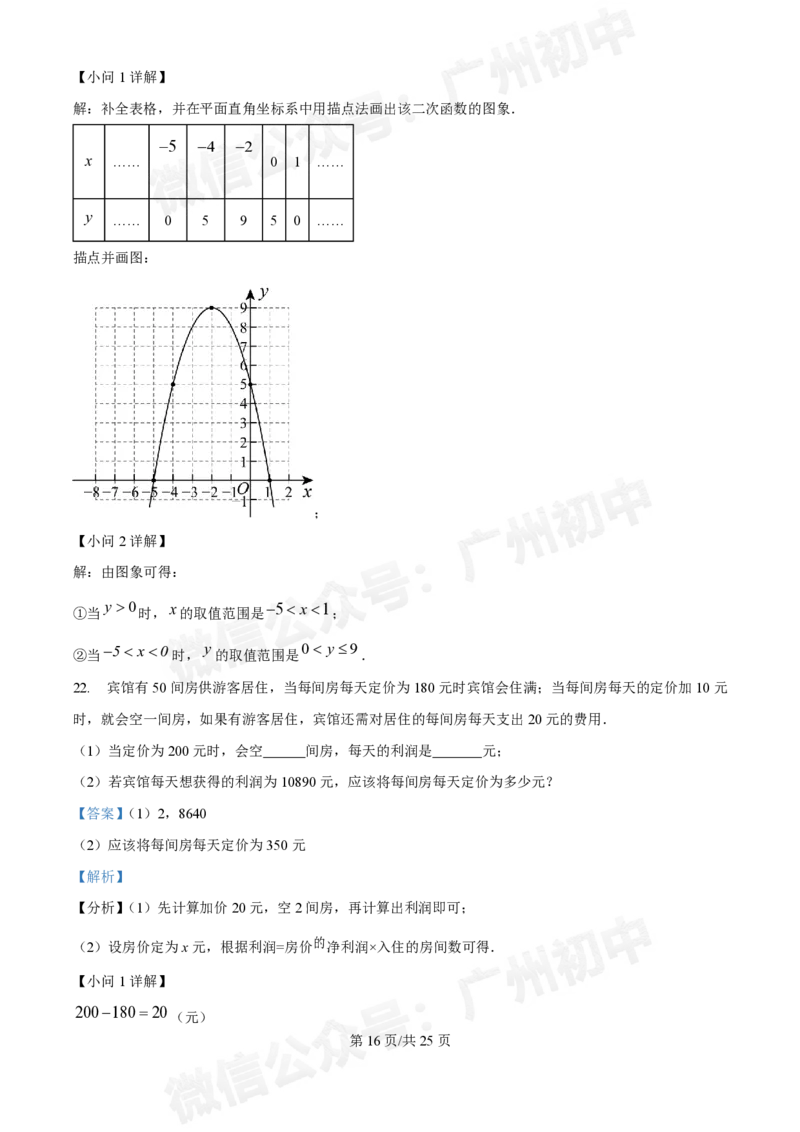已知二次函数 ． （1）补全表格，并在平面直角坐标系中用描点法画出该二次函数的图象． 5 4 2 x … 0 1 … y … 0 5 9 … （2）根据图象回答下列问题： y 0 ①当 时，x的取值范围是 ； ②当5 x0时，y的取值范围是 ． 【答案】（1）画图见解析 5 x1 0 y9 （2）① ，② ； 【解析】 【分析】本题考查的是二次函数的性质，画二次函数的图象； x0 x1 （1）把 ， 分别代入抛物线的解析式，先填表格，再描点画图即可； x （2）①直接根据二次函数的图象在 轴上方的部分对应的范围可得答案；②直接根据图象在 5 x0间的部分对应的函数值可得答案． 第15页/共25页 学科网（北京）股份有限公司【小问1详解】 解：补全表格，并在平面直角坐标系中用描点法画出该二次函数的图象． 5 4 2 x …… 0 1 …… y …… 0 5 9 5 0 …… 描点并画图： ； 【小问2详解】 解：由图象可得： y 0 x 5 x1 ①当 时， 的取值范围是 ； ②当5 x0时， y 的取值范围是 0 y9 ． 22. 宾馆有50间房供游客居住，当每间房每天定价为180元时宾馆会住满；当每间房每天的定价加10元 时，就会空一间房，如果有游客居住，宾馆还需对居住的每间房每天支出20元的费用． （1）当定价为200元时，会空 间房，每天的利润是 元； （2）若宾馆每天想获得的利润为10890元，应该将每间房每天定价为多少元？ 【答案】（1）2，8640 （2）应该将每间房每天定价为350元 【解析】 【分析】（1）先计算加价20元，空2间房，再计算出利润即可； 的 （2）设房价定为x元，根据利润=房价 净利润×入住的房间数可得． 【小问1详解】 20018020 （元） 第16页/共25页 学科网（北京）股份有限公司20÷10=2（间） (502)(20020)8640 所以，每天的利润为： （元） 故答案为：2，8640； 【小问2详解】 解：设房价定为x元， x180 (x20)(50 )10890 根据题意，得 10 ． x2 700x1225000 整理，得 ， x  x 350 解得 1 2 ． 答：应该将每间房每天定价为350元． 【点睛】此题考查了一元二次方程的应用，解题的关键是理解题意找到题目蕴含的相等关系． 23. 鹰眼技术助力杭州亚运，提升球迷观赛体验．如图分别为足球比赛中某一时刻的鹰眼系统预测画面 OA （如图1）和截面示意图（如图2），攻球员位于点O，守门员位于点A， 的延长线与球门线交于点 B，且点A，B均在足球轨迹正下方，足球的飞行轨迹可看成抛物线．水平距离s与离地高度h的鹰眼数据 如表： s/m 0 9 12 15 18 21 … 4.2 4.2 h/m 0 4.8 5 4.8 … s  （1）根据表中数据预测足球落地时， ______m； （2）求h关于s的函数解析式； （3）当守门员位于足球正下方，足球离地高度不大于守门员的最大防守高度2.6m时，视为防守成功，若 s 24m 一次防守中，守门员位于足球正下方时， ，请问这次守门员能否防守成功？试通过计算说明． 1 2 h s2  s 【答案】（1）30 （2） 45 3 第17页/共25页 学科网（北京）股份有限公司（3）守门员不能成功防守，理由见解析． 【解析】 【分析】本题考查的是二次函数的实际应用，利用待定系数法求解二次函数的解析式，理解题意，明确函 数图象上点的横坐标与纵坐标的含义是解本题的关键． （1）根据抛物线的对称轴可直接得出结论； 12,4.8 （2）根据抛物线的对称性找到顶点，设出顶点式，再代入 可求出参数，由此可解答； s 24 h （3）把 代入二次函数解析式求出 ，再与最大防守高度比较即可． 【小问1详解】 解：由表格可知， s 9 时和 s 21 时， h 相等，s =12时，s =18时， h 相等， s15 抛物线关于 对称， Q当 s 0 时， h0 ， s 30 h0 时， ； 【小问2详解】 s15 ha(s15)2 5 由（1）知，抛物线关于 对称，设 ， 12,4.8 把 代入上述解析式， 1 a  a(1215)2 54.8 ，解得 45， 1 1 2 h (s15)2 5 s2  s. 45 45 3 【小问3详解】 s 24m 当 ， 1 1 h (s15)2 5 92 51.853.22.6 45 45 ∴ ， ∴守门员不能成功防守． y  x2 2mxm1 24. 已知抛物线G： 中． 0，0 （1）若抛物线G经过点 ，求抛物线G的解析式和顶点坐标； 1，0 180 （2）把抛物线G绕点 旋转 得到抛物线H， An2,p B2,q Cn, p pqm2 ①若点 ， ， 都在抛物线H上且 ，求n的取值范围； 第18页/共25页 学科网（北京）股份有限公司②已知抛物线H恒过定点P，记抛物线H的顶点为点Q，当m的值变化时，点Q的运动轨迹为曲线W， l l 直线 过点P且与曲线W有且只有一个公共点，求直线 的解析式． y  x2 2x  1，1  【答案】（1）抛物线的解析式为 ，顶点坐标为 5 3 x y  （2）① n2 ；② 2 或 4 【解析】 【分析】本题考查了二次函数的图象与性质，旋转的性质，二次函数解析式等知识．熟练掌握二次函数的 图象与性质，旋转的性质，二次函数解析式是解题的关键． 0，0 y  x2 2xx12 1 m10 m1 （1）由抛物线G经过点 ，可得 ，可求 ，则 ，进而可得抛 物线的解析式和顶点坐标； 1，0 180 x，y （2）①由抛物线G绕点 旋转 得到抛物线H，抛物线H上的坐标设为 ，则抛物线G上的 2x， y y 2x2 2m2xm1 坐标为 ，则 ，进而可得抛物线H解析式为 2m2 x m2 y x2 2m2x5m3 21 ，对称轴为直线 ，由a10，可知图象开口向 An2,p B2,q Cn, p 下，图象上的点离对称轴越近，函数值越大，由点 ， ， 都在抛物线H上，可 n2n x n1 得对称轴为直线 2 ，则 m2n1 ，即 mn3 ，由题意知， q 22 2m225m3m1n4 p q m2n5 ，由 ，可得 nn1  2n1 y x2 4xm2x53 n4n5 ， ，计算求解即可；②由 ，可知当 5 3 5 3 x y  P  ，  2 时， 4 ，即抛物线H恒过定点 2 4 ，当 x m2 时， y m2 m1 ，则抛物线H的顶  m2，m2 m1  m2t m2 m1s mt2 Qt，s 点为点Q ，令 ， ，则 ， ，可求得 2  5 3 s t2 5t23t2 5t7 t     2 4 ，即点Q的运动轨迹为曲线W为二次函数；且顶点坐标 5 3 5 3 5  ，   ，  x 2 4 l 2 4 l 2 为 ，由直线 过点P 且与曲线W有且只有一个公共点，可得直线 的解析式为 或 3 y  4 ． 【小问1详解】 第19页/共25页 学科网（北京）股份有限公司0，0 解：∵抛物线G经过点 ， m10 ∴ ， m1 解得， ， y  x2 2xx12 1 ∴ ， y  x2 2x  1，1  ∴抛物线的解析式为 ，顶点坐标为 ； 【小问2详解】 1，0 180 ①解：∵抛物线G绕点 旋转 得到抛物线H， x，y 2x， y ∴抛物线H上的坐标设为 ，则抛物线G上的坐标为 ， y 2x2 2m2xm1 ∴ ， y x2 2m2x5m3 整理得， ， y x2 2m2x5m3 ∴抛物线H解析式为 ， 2m2 x m2 21 ∴对称轴为直线 ， ∵a10， ∴图象开口向下，图象上的点离对称轴越近，函数值越大， An2,p B2,q Cn, p ∵点 ， ， 都在抛物线H上， n2n x n1 ∴对称轴为直线 2 ， m2n1 mn3 ∴ ，即 ， q 22 2m225m3m1n4 由题意知， ， p q m2n5 ∵ ， nn1  2n1 n4n5 ∴ ， ， 9 n 解得， n4 或 n2 ， 2 ， n2 ∴n的取值范围为 ； y x2 4xm2x53 ②解：∵ ， 第20页/共25页 学科网（北京）股份有限公司5 3 x y  ∴当 2 时， 4 ， 5 3 P ，   2 4 ∴抛物线H恒过定点 ， x m2 y m2 m1 当 时， ，  m2，m2 m1  ∴抛物线H的顶点为点Q ， m2t m2 m1s mt2 Qt，s 令 ， ，则 ， ， m2 m1m22 5m3 ∵ ， 2  5 3 s t2 5t23t2 5t7 t     2 4 ∴ ， 5 3 ，   2 4 ∴点Q的运动轨迹为曲线W为二次函数；且顶点坐标为 ， 5 3 ，   l 2 4 ∵直线 过点P 且与曲线W有且只有一个公共点， 5 3 x y  ∴直线 l 的解析式为 2 或 4 ． 25. 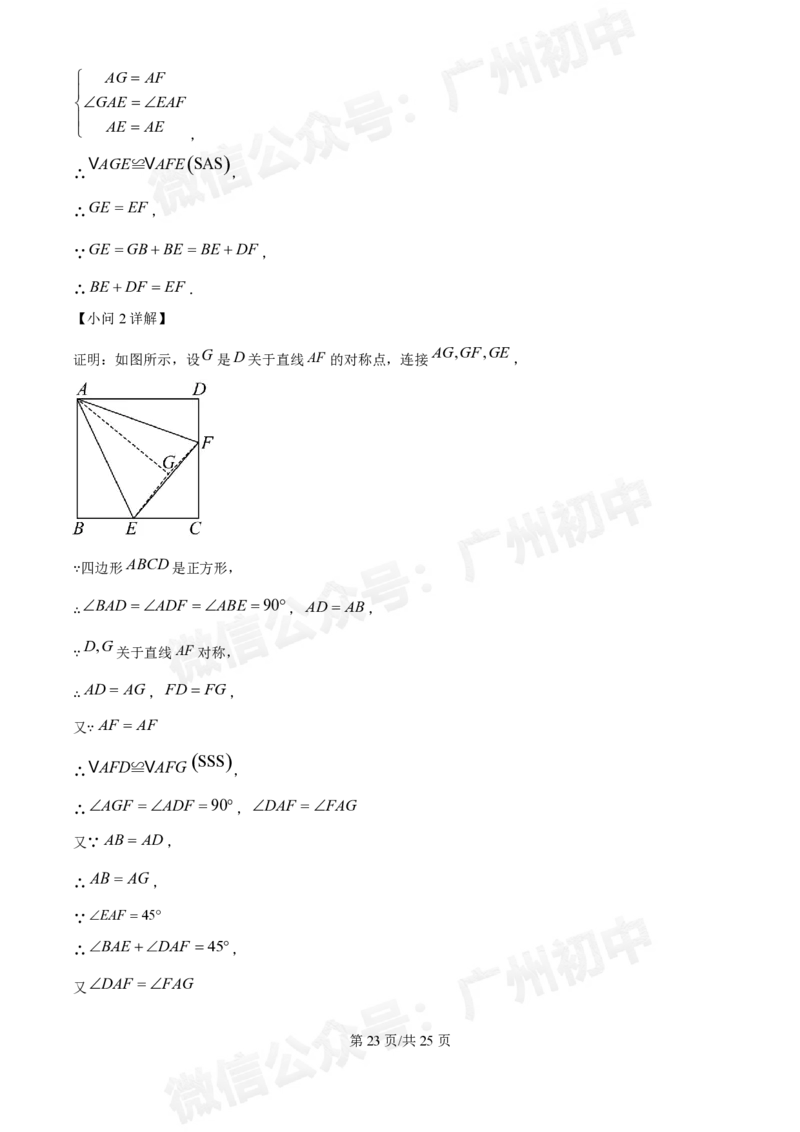已知正方形 ABCD ，点E，F 分别在边 BC ，𝐶𝐷上，连接AE，AF ，EF ，EAF 45 （1）求证：BEDF  EF ； （2）记点D关于直线AF 的对称点为点 G ，求证：直线EF 恒过点 G ； （3）连接𝐵𝐷，分别交AE，AF 于点P， Q ，若AB 1，求 PQ 长度的最小值． 【答案】（1）见解析 （2）见解析 2 2 （3） 【解析】 第21页/共25页 学科网（北京）股份有限公司VADF≌VABGSAS 【分析】（1）延长𝐶𝐵到点G，使 BG  DF ，连接 AG ，证明 ，由全等三角形的性 VAGE≌VAFESAS AF  AG，DAF BAG 质得出 ，证明 ，由全等三角形的性质得出 GE  EF ，则可得出结论； （2）设 G 是D关于直线AF 的对称点，连接 AG,GF,GE ，证明 VAFD≌VAFG SSS ， SAS VABE≌VAGE 得出AGF AGE 90，即可得证； （3）将△ADQ 绕点A顺时针旋转90°，得到VABG，连接 BG，GP ，得出 VGAP≌VQAPSAS ，进而 GBP 90 GP2  BG2 BP2 PQ2 GP2  BG2 BP2 2BGBP 得出 ，则 ，根据 ，当 BG  BP 时取得等于号，得出 BPQD ,时取得最小值，进而勾股定理求得BP的长，即可求解． 【小问1详解】 证明：延长𝐶𝐵到点G，使 BG  DF ，连接 AG ， AD AB，ABG ADF 90 ∵ ， VADF≌VABGSAS ∴ ， AF  AG，DAF BAG ∴ ， ABCD ∵四边形 为正方形， ∴BAD90， ∵EAF 45， ∴BAEDAF 45， BAGBAE＝45EAF ∴ ， 在 VAGE 和△AFE中， 第22页/共25页 学科网（北京）股份有限公司 AG  AF  GAE EAF  AE  AE  ， VAGE≌VAFESAS ∴ ， GE  EF ∴ ， GE GBBE  BEDF ∵ ， ∴BEDF  EF ． 【小问2详解】 证明：如图所示，设 G 是D关于直线AF 的对称点，连接 AG,GF,GE ， ABCD ∵四边形 是正方形， ∴ BADADF ABE 90 ，AD AB， D,G ∵ 关于直线AF 对称， ∴ AD AG ，FD FG， 又∵ AF  AF SSS VAFD≌VAFG ∴ ， AGF ADF 90 DAF FAG ∴ ， 又∵AB AD， AB AG ∴ ， ∵EAF 45 ∴BAEDAF 45， DAF FAG 又 第23页/共25页 学科网（北京）股份有限公司FAGBAE 45 ∴ ， ∴BAEFAD45， BAE GAE ∴ AB  AG,AE  AE 又∵ SAS ∴ VABE≌VAGE ∴AGE ABE 90 ∴AGF AGE 90 ∴ G 在EF 上， 即直线EF 恒过点 G ； 【小问3详解】 解：∵四边形 ABCD 是正方形，BD是对角线， ADQ45 ∴ 将△ADQ 绕点A顺时针旋转90°，得到VABG，连接 BG，GP ， DQ BG，ADQABG 45 ∴ ， ∵EAF 45， DAQBAP45 ∴ ， BAGBAPGAP45 ∴ ， GAPQAP ∴ ， ∵AP AP， VGAP≌VQAPSAS ∴ ， GP PQ ∴ ， 第24页/共25页 学科网（北京）股份有限公司ABG ABP45 ∵ ， GBP 90 GP2  BG2 BP2 ∴ ，则 BG2 BP2 2BGBPBGBP2 0 又∵ PQ2 GP2  BG2 BP2 2BGBP BG  BP BPQD ∴ ，当 时取得等于号，即 , ∵AB 1 BD 2 ∴ ， BPQD x PQ 22xGP 设 ，则 GP2  BG2 BP2 ∵  2 x2 x2  22x ∴ x 21 PG0 x 21 解得： （舍去，此时 ）或   PQ 22 21 2 2 即 PQ 2 2 ∴ 的最小值为 【点睛】本题考查了正方形的性质，全等三角形的性质与判定，旋转的性质，勾股定理，熟练掌握以上知 识是解题的关键． 第25页/共25页 学科网（北京）股份有限公司