文档内容
广州市香江中学 2024-2025 学年度第一学期综合练习 1
九年级数学科试题
出卷:何莉亚 审核:林莉
说明:
1、本试卷分为选择部分和非选择部分,全卷共三大题25小题,共120分。考试时间120分
钟。
2、答题前,考生务必将自己的姓名、考生号、考试科目用2B铅笔涂在答题卡上。
3、本卷分“问卷”和“答卷”,本试卷选择题部分必须填在答题卡上,否则不给分;非选
择题部分的试题,学生在解答时必须将答案写在“答卷”上指定的位置(方框) 内,写在其他地
方答案无效,“问卷”上不可以用来答题;
4、考试结束后,考生须将本试卷和答题卡一并交回;
5、考生解答填空题和解答题必须用黑色字迹钢笔或签字笔作答,如用铅笔作答的试题一律
以零分计算;
6、选择题要求用规定型号铅笔填涂,涉及作图的题目,用题目中规定型号的铅笔作图。
一、选择题(每题3分,共30分)
1. 若关于 x的一元二次方程为 3𝑥²‒5𝑥+1=0, 它的二次项系数和一次项系数分别为( )
A. 3, 5 B. 3, 1 C. 3x², -5x D. 3, -5
2. 关于二次函数 𝑦=2(𝑥‒4)²+6,下列说法正确的是 ( )
A. 最大值4 B. 最小值4 C. 最大值6 D. 最小值6
3.抛物线 𝑦=𝑥²+4𝑥的对称轴是直线 ( )
A. x=2 B. x=-2 C. x=3
1
𝐷.𝑥 =‒
2
4.如图是四种正多边形的瓷砖图案. 其中是轴对称图形但不是中心对称图形的是( )
A. ①② B. ②③ C. ①③ D.②④
5.用配方法解一元二次方程 𝑥²‒8𝑥+5=0,将其化成( (𝑥+𝑎)²=𝑏的形式,则变形正确的是( )
𝐴.(𝑥+4)²=11 𝐵.(𝑥‒4)²=21 𝐶.(𝑥‒8)²=11
𝐷.(𝑥‒4)²=11
6.将二次函数 𝑦=𝑥²的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是(
)
𝐴.𝑦=(𝑥‒1)²+2 𝐵.𝑦=(𝑥+1)²+2
𝐶.𝑦=(𝑥‒1)²‒2 𝐷.𝑦=(𝑥+1)²‒27. 若二次函数 𝑦=𝑎𝑥²‒2𝑎𝑥+𝑐的图象经过点(-1,0),则方程 𝑎𝑥²‒2𝑎𝑥+𝑐=0的解为( )
A. x=-1 𝐵.𝑥₁=3,𝑥₂=1
𝐶.𝑥₁=‒1,𝑥₂=‒3 𝐷.𝑥₁=3,𝑥₂=‒1
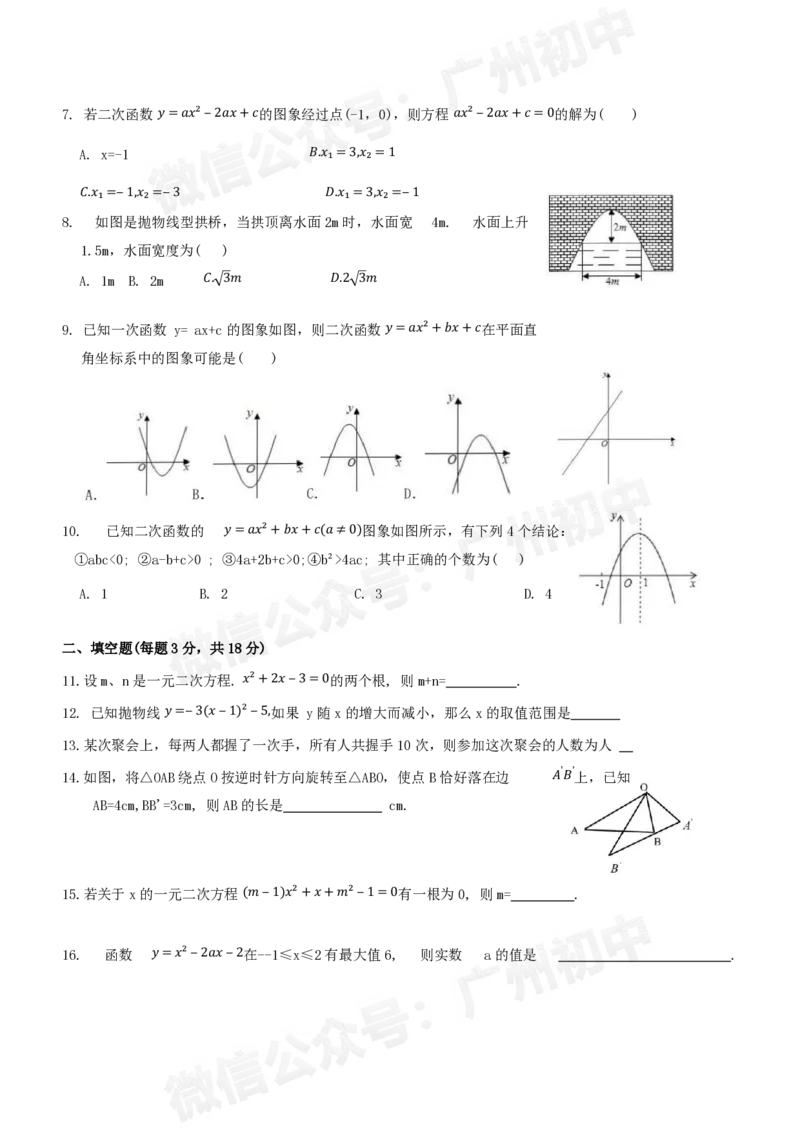
8. 如图是抛物线型拱桥,当拱顶离水面2m时,水面宽 4m. 水面上升
1.5m,水面宽度为( )
A. 1m B. 2m 𝐶. 3𝑚 𝐷.2 3𝑚
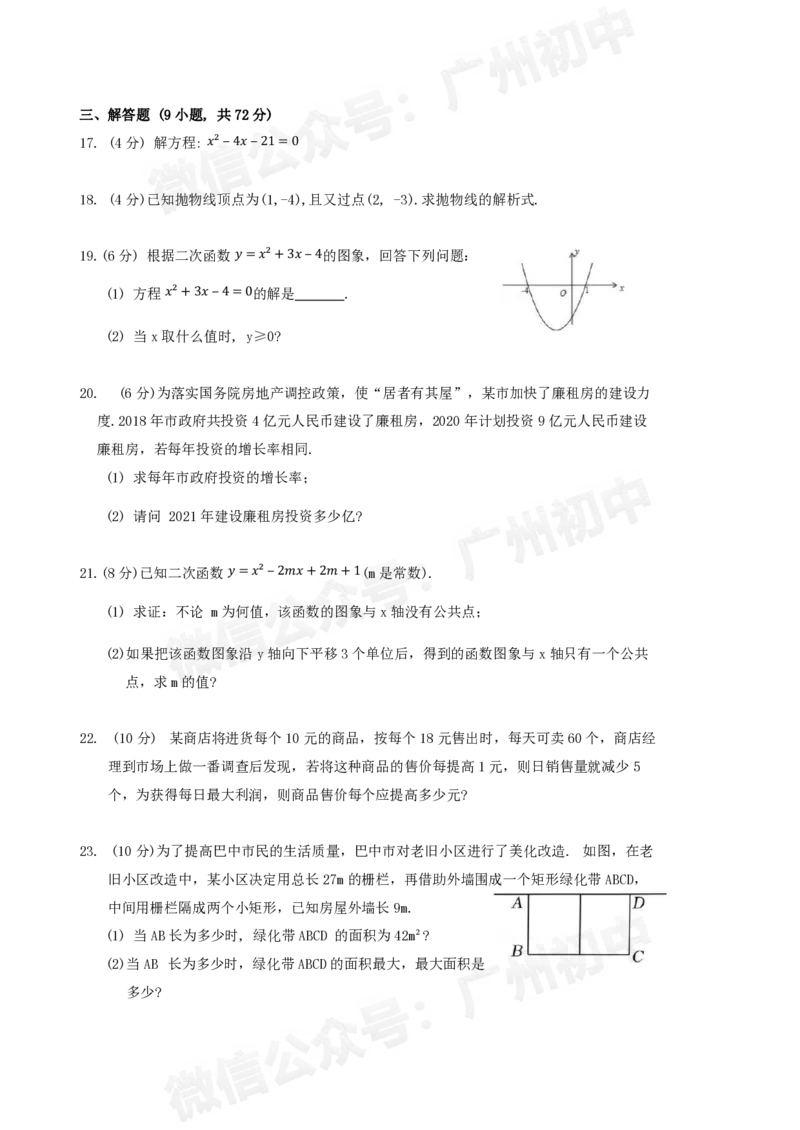
9. 已知一次函数 y= ax+c的图象如图,则二次函数 𝑦=𝑎𝑥²+𝑏𝑥+𝑐在平面直
角坐标系中的图象可能是( )
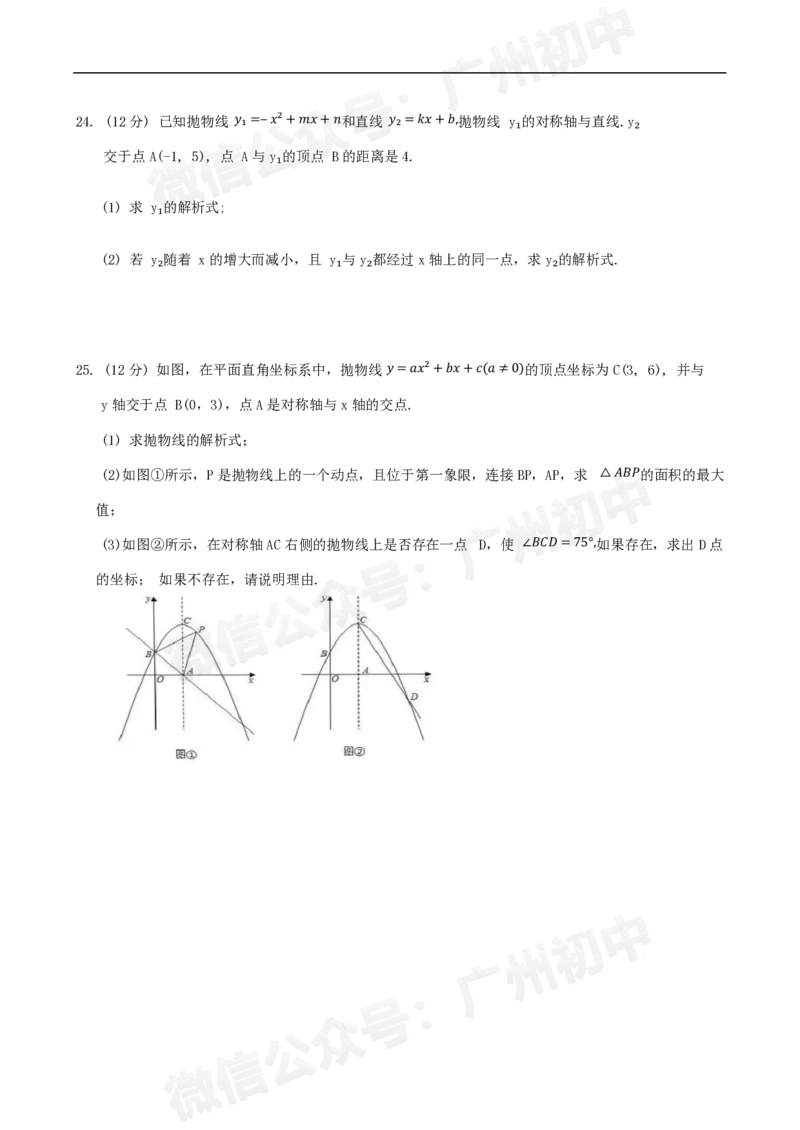
10. 已知二次函数的 𝑦=𝑎𝑥²+𝑏𝑥+𝑐(𝑎≠0)图象如图所示,有下列4个结论:
①abc<0; ②a-b+c>0 ; ③4a+2b+c>0;④b²>4ac; 其中正确的个数为( )
A. 1 B. 2 C. 3 D. 4
二、填空题(每题3分,共18分)
11.设m、n是一元二次方程. 𝑥²+2𝑥‒3=0的两个根, 则m+n= .
12. 已知抛物线 𝑦=‒3(𝑥‒1)²‒5,如果 y随x的增大而减小,那么x的取值范围是
13.某次聚会上,每两人都握了一次手,所有人共握手10次,则参加这次聚会的人数为人
14.如图,将△OAB绕点O按逆时针方向旋转至△ABO,使点B恰好落在边
𝐴'𝐵'
上,已知
AB=4cm,BB'=3cm, 则AB的长是 cm.
15.若关于x的一元二次方程 (𝑚‒1)𝑥²+𝑥+𝑚²‒1=0有一根为0, 则m= .
16. 函数 𝑦=𝑥²‒2𝑎𝑥‒2在--1≤x≤2有最大值6, 则实数 a的值是 .三、解答题 (9小题, 共72分)
17. (4分) 解方程: 𝑥²‒4𝑥‒21=0
18. (4分)已知抛物线顶点为(1,-4),且又过点(2, -3).求抛物线的解析式.
19.(6分) 根据二次函数 𝑦=𝑥²+3𝑥‒4的图象,回答下列问题:
(1) 方程 𝑥²+3𝑥‒4=0的解是 .
(2) 当x取什么值时, y≥0?
20. (6分)为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房的建设力
度.2018年市政府共投资4亿元人民币建设了廉租房,2020年计划投资9亿元人民币建设
廉租房,若每年投资的增长率相同.
(1) 求每年市政府投资的增长率;
(2) 请问 2021年建设廉租房投资多少亿?
21.(8分)已知二次函数 𝑦=𝑥²‒2𝑚𝑥+2𝑚+1(m是常数).
(1) 求证:不论 m为何值,该函数的图象与x轴没有公共点;
(2)如果把该函数图象沿y轴向下平移3个单位后,得到的函数图象与x轴只有一个公共
点,求m的值?
22. (10分) 某商店将进货每个10元的商品,按每个18元售出时,每天可卖60个,商店经
理到市场上做一番调查后发现,若将这种商品的售价每提高1元,则日销售量就减少5
个,为获得每日最大利润,则商品售价每个应提高多少元?
23. (10分)为了提高巴中市民的生活质量,巴中市对老旧小区进行了美化改造. 如图,在老
旧小区改造中,某小区决定用总长27m的栅栏,再借助外墙围成一个矩形绿化带ABCD,
中间用栅栏隔成两个小矩形,已知房屋外墙长9m.
(1) 当AB长为多少时, 绿化带ABCD 的面积为42m²?
(2)当AB 长为多少时,绿化带ABCD的面积最大,最大面积是
多少?24. (12分) 已知抛物线 𝑦₁=‒𝑥²+𝑚𝑥+𝑛和直线 𝑦₂=𝑘𝑥+𝑏,抛物线 y₁的对称轴与直线.y₂
交于点A(-1, 5), 点 A与y₁的顶点 B的距离是4.
(1) 求 y₁的解析式;
(2) 若 y₂随着 x的增大而减小,且 y₁与y₂都经过x轴上的同一点,求y₂的解析式.
25. (12分) 如图,在平面直角坐标系中,抛物线 𝑦=𝑎𝑥²+𝑏𝑥+𝑐(𝑎≠0)的顶点坐标为C(3, 6), 并与
y轴交于点 B(0,3),点A是对称轴与x轴的交点.
(1) 求抛物线的解析式;
(2)如图①所示,P是抛物线上的一个动点,且位于第一象限,连接BP,AP,求 △𝐴𝐵𝑃的面积的最大
值;
(3)如图②所示,在对称轴AC右侧的抛物线上是否存在一点 D,使 ∠𝐵𝐶𝐷=75°,如果存在,求出D点
的坐标; 如果不存在,请说明理由.
学科网(北京)股份有限公司