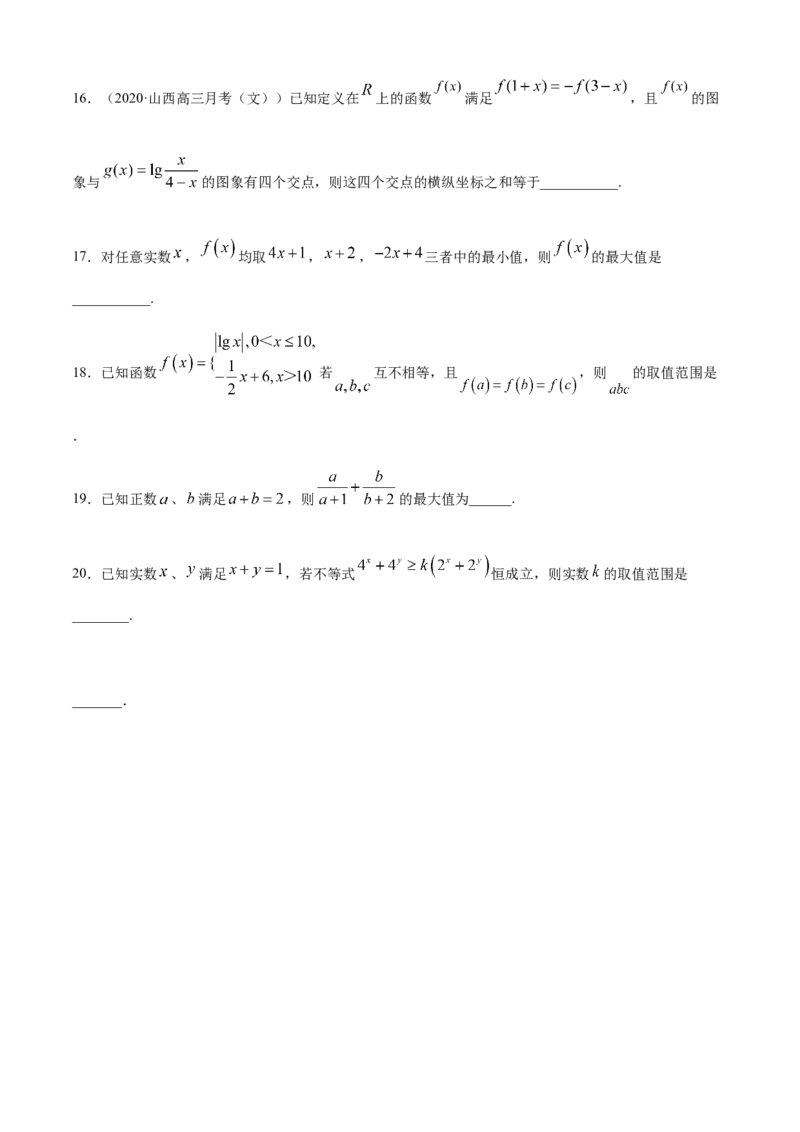文档内容
专练 06(填空题-压轴)
1.已知直线 经过点 ,则 的最小值是__.
2.已知函数 在区间 上是增函数,且 .若 ,且
,则实数 的取值范围是__________.
3.已知函数 在区间 上是减函数,则实数 的取值范围是_____.
4.已知点 在函数 ( 且 )图象上,对于函数 定义域中的任意 ,
,有如下结论:
① ;② ;
③ ;④ .
上述结论中正确结论的序号是___________.
5.已知函数 , , , ,使得
成立,则实数 的取值范围为_____________.
6.(2020·广西南宁二中高一期中)设函数 则使得f( )>f(3x-1)成立的x的
取值范围是___________.7.若函数 满足对任意 ,都有 成立,则实数 的
取值范围是______.
8.(2018·江苏省南通中学高一)已知函数 的最大值是 ,最小值为 ,
则 __.
9.(2015·上海市延安中学高一期中)已知关于 的不等式 的解集为 ,则实数 的取值
范围是__________.
10.(2018·福建高一期中)函数 有四个零点,则 的取值范围为_______.
11.已知函数 的值域为 ,则实数 的取值范围是_____ .
12.已知 ,则不等式 的解集是________.
13.已知 ,则 ________.
14.某企业准备投入适当的广告费对甲产品进行促销宣传,在一年内预计销量 (万件)与广告费 (万
元)之间的函数关系为 ,已知生产此产品的年固定投入为 万元,每生产1万件此产
品仍需要再投入30万元,且能全部销售完,若每件甲产品销售价格(元)定为:“平均每件甲产品生产成
本的150%”与“年平均每件产品所占广告费的50%”之和,则当广告费为1万元时,该企业甲产品的年利润
比不投入广告费时的年利润增加了__________万元.
15.已知 , ,则 的最小值为_______.16.(2020·山西高三月考(文))已知定义在 上的函数 满足 ,且 的图
象与 的图象有四个交点,则这四个交点的横纵坐标之和等于___________.
17.对任意实数 , 均取 , , 三者中的最小值,则 的最大值是
___________.
18.已知函数 若 互不相等,且 ,则 的取值范围是
.
19.已知正数 、 满足 ,则 的最大值为______.
20.已知实数 、 满足 ,若不等式 恒成立,则实数 的取值范围是
________.
_______.