文档内容
专练 06(填空题-压轴)
1.已知直线 经过点 ,则 的最小值是__.
【答案】32
【分析】
根据题意,由直线经过点 ,分析可得 ,即 ;进而可得
,结合基本不等式分析可得答案.
【详解】
根据题意,直线 经过点 ,则有 ,即 ;
则 ,当且仅当 时等号成立;
即 的最小值是32;
故答案为:32.
【点睛】
本题考查基本不等式的性质以及应用,涉及直线的一般式方程,属于中档题.
2.已知函数 在区间 上是增函数,且 .若 ,且,则实数 的取值范围是__________.
【答案】
【分析】
利用赋值法求出 ,且 ,然后利用函数的单调性即可解不等式.
【详解】
在 中,令 ,得 ,
所以 .令 , ,得 ,
再令 , ,得 .
又因为 ,所以 可化为 ,
即 ,所以 ,解得 .
故答案为:
【点睛】
本题考查了抽象函数的单调性解不等式,注意在解不等式时需在定义域内求解,属于基础题.
3.已知函数 在区间 上是减函数,则实数 的取值范围是_____.【答案】
【分析】
根据复合函数单调性的性质,结合二次函数单调性与对数定义域要求,分类讨论 与 两种情
况,即可求得 的取值范围.
【详解】
函数 ,所以 且 ,
令 ,则
当 时,因为函数 在 内单调递减,而函数 在区间 上是减函数,由
复合函数单调性的性质可知, 在区间 上是增函数,
由二次函数对称轴及单调性可得 .且满足对数函数定义域要求,即 ,解得
,所以由以上可得 ;
当 时,因为函数 在 内单调递增,而函数 在区间 上是减函数,由复合
函数单调性的性质可知, 在区间 上是减函数,
由二次函数对称轴及单调性可得 .且满足对数函数定义域要求,即 ,解得
,所以由以上可得 .
综上可知, 的取值范围为 .故答案为: .
【点睛】
本题考查了复合函数单调性性质应用,对数函数定义域要求,二次函数的对称性及单调性,分类讨论思想
的综合应用,属于中档题.
4.已知点 在函数 ( 且 )图象上,对于函数 定义域中的任意 ,
,有如下结论:
① ;② ;
③ ;④ .
上述结论中正确结论的序号是___________.
【答案】①④
【分析】
先求出a,根据指数运算与指数函数性质依次讨论即可逐项排除得到答案.
【详解】
点 在函数 ( 且 )图象上,即 , , ,
∵对于函数 定义域中的任意的 ,
有
∴结论(1)正确;又 , , ,
∴结论(2)错误;
又 是定义域 上的增函数,
∴对任意的 ,不妨设 ,则 , , ,
,
∴结论(3)错误;
又 ,
,
,
∴结论(4)正确;
故答案为:(1),(4).
【点晴】
本题考查命题真假判断,实质上是考查函数的性质.对于这种给出具体函数式的问题,只要把函数式代入
一一验证即可,解决此类问题不能限入误区,认为这类问题都是有难度,没处下手,事实上最简单的方法
反而是最好的方法.5.已知函数 , , , ,使得
成立,则实数 的取值范围为_____________.
【答案】
【分析】
对于 , ,使得 成立,则有 ,利用函数的单调性分
别在定义域内求出最值即可.
【详解】
由 ,
根据复合函数的单调性可得 在 上单调递减,在 上单调递增,
所以
对于 , ,使得 成立,则有
即不等式 ,对于任意的 恒成立.
当 时, ,对于任意的 , 恒成立,
符合题意;当 时, 的图像是开口向下的抛物线,且
要使不等式 对于任意的 恒成立,
则若对称轴 ,即 , ,即 ,显然成立,
若对称轴 ,即 时, ,
解得 ,故 ,
此时 ,
当 时,函数 的图像是开口向上的抛物线,
对称轴方程为 ,
在 上无最大值,故不符合题意,
综上所述,实数 的取值范围为 .
故答案为:
【点睛】
本题主要考查考查了不等式恒成立问题、考查了二次函数在某个区间上的最值,符合函数的单调性,考查
了分类讨论的思想,属于中档题.6.(2020·广西南宁二中高一期中)设函数 则使得f( )>f(3x-1)成立的x的
取值范围是___________.
【答案】
【分析】
先判断函数的奇偶性,求出函数的单调性,由此得到 ,解不等式即得解.
【详解】
由题得函数的定义域为R. 所以函数是偶函数.
当 时, 都是增函数,所以 是增函数,
所以函数在 是增函数,在 上是减函数.
因为f( )>f(3x-1),所以 .
故答案为:
【点睛】
本题主要考查函数的奇偶性和单调性的判断,考查抽象不等式的解法,注意对于偶函数,解其不等式时,
避免讨论,运用绝对值得出其大小关系,属于中档题.7.若函数 满足对任意 ,都有 成立,则实数 的
取值范围是______.
【答案】
【分析】
根据题中条件,可以先判断出函数f(x)在R上单调递增,再结合分段函数的解析式,要每一段都是增函
数,且分界点时右段函数的函数值要大于等于左段函数的函数值,列出不等关系,求解即可得到a的取值
范围.
【详解】
:∵对任意x≠x,都有 成立,
1 2
∴x-x 与f(x)-f(x)同号,
1 2 1 2
根据函数单调性的定义,可知f(x)在R上是单调递增函数,
∴当 时,f(x)=( 为增函数,则 ,即a<3,①
且当x=2时,有最小值 ;
当 时,f(x)= 为二次函数,图象开口向下,对称轴为x=2,
若f(x)在(-∞,2)上为增函数,且 ;
又由题意,函数在定义域R上单调递增,
则 ,解得 ;②
综合①②可得a的取值范围: ,即答案为 .
【点睛】
本题考查了分段函数的单调性的问题,一般选用分类讨论和数形结合的思想方法进行求解.注意解题方法
的积累,属于中档题.
8.(2018·江苏省南通中学高一)已知函数 的最大值是 ,最小值为 ,
则 __.
【答案】2
【分析】
化简函数可得 ,可判 为奇函数,由奇函数的性质可得结论.
【详解】
解: ,
令 ,可得 ,
函数 为奇函数,
的最大值与最小值之和为0,
的最大值与最小值之和为2,即 ,
故答案为:2【点睛】
本题考查函数的奇偶性与最值,突出考查转化思想、创新思维与综合运算能力,属中档题.
9.(2015·上海市延安中学高一期中)已知关于 的不等式 的解集为 ,则实数 的取值
范围是__________.
【答案】
【分析】
不等式等价于 的解集是 ,分 和 两种情况讨论求实数 的取值范围.
【详解】
恒成立, 不等式等价于 的解集是 ,
当 时, 不成立,解集是 ,
当 时, ,解得: ,
综上: .
故答案为:
【点睛】
本题考查根据不等式的解集求参数的取值范围,意在考查分类讨论和计算能力,属于基础题型.
10.(2018·福建高一期中)函数 有四个零点,则 的取值范围为_______.【答案】
【分析】
函数零点转化为 的解,即函数 与直线 的交点的横坐标,由数形
结合思想可得解.
【详解】
由 得 ,作函数 的图象和直线 ,如图,
函数 在 和 上递减,在 和 上递增, ,由图象知当 时,
的图象和直线 有四个交点.即 有4个零点.
故答案为: .
【点睛】
本题考查函数的零点个数,解题时把问题转化为函数图象与直线交点个数,通过数形结合思想求解.
11.已知函数 的值域为 ,则实数 的取值范围是_____.
【答案】【分析】
根据整个函数值域为R及分段函数右段的值域,可判断出左段的函数为单调性递增,且最大值大于等于1,即
可求得 的取值范围.
【详解】
当 时, ,此时值域为
若值域为 ,则当 时. 为单调递增函数,且最大值需大于等于1
即 ,解得 ,故答案为:
【点睛】
本题考查了分段函数值域的关系及判断,指数函数的性质与一次函数性质的应用,属于中档题.
12.已知 ,则不等式 的解集是________.
【答案】
【分析】
先构造函数 ,得到 关于 对称,且单调递增,再结合对称性与
单调性将不等式 转化为 即可求解.
【详解】
构造函数 ,那么 是单调递增函数,
且向左移动一个单位得到 ,的定义域为 ,且 ,
所以 为奇函数,图象关于原点对称,所以 图象关于 对称.
不等式 等价于 ,
等价于
结合 单调递增可知 ,
所以不等式 的解集是 , .
故答案为: , .
【点睛】
本题主要考查函数的奇偶性和单调性的应用,考查函数的对称性的应用,意在考查学生对这些知识的理解
掌握水平.
13.已知 ,则 ________.
【答案】
【分析】
等式平方相加得到 ,解得答案.
【详解】由 平方相加得 ,
即 .
故答案为: .
【点睛】
本题考查了三角恒等变换,意在考查学生的计算能力和转化能力.
14.某企业准备投入适当的广告费对甲产品进行促销宣传,在一年内预计销量 (万件)与广告费 (万
元)之间的函数关系为 ,已知生产此产品的年固定投入为 万元,每生产1万件此产
品仍需要再投入30万元,且能全部销售完,若每件甲产品销售价格(元)定为:“平均每件甲产品生产成
本的150%”与“年平均每件产品所占广告费的50%”之和,则当广告费为1万元时,该企业甲产品的年利润
比不投入广告费时的年利润增加了__________万元.
【答案】
【解析】
由题意可得,当广告费为 万元时, ,产品的生产成本为 (万元),每件销售价为
(元), 年销售收入为 (万元), 年利润为
(万元),若不投入广告费,则 ,产品的生产成本为 (万元),每
件销售价为 (元), 年销售收入为 (万元), 年利润为 (万元),故企业甲产品的年利润比不投入广告费时的年利润增加了 万元,故答案为 .
15.已知 , ,则 的最小值为_______.
【答案】
【分析】
由 ,两次利用基本不等式即可求解.
【详解】
由 , , ,
当且仅当 , 时取等号,故答案为:
【点睛】
本题考查了基本不等式求最值,注意等号成立的条件,属于中档题.
16.(2020·山西高三月考(文))已知定义在 上的函数 满足 ,且 的图
象与 的图象有四个交点,则这四个交点的横纵坐标之和等于___________.
【答案】8
【分析】
确定 的图象关于点 对称,函数 的图象关于点 对称,得到答案.【详解】
,故 ,即 的图象关于点 对称,
又函数 满足 ,则函数 的图象关于点 对称,
所以四个交点的横纵坐标之和为8.
故答案为:8.
【点睛】
本题考查了函数的交点问题,确定函数关于点 对称是解题的关键.
17.对任意实数 , 均取 , , 三者中的最小值,则 的最大值是
___________.
【答案】
【分析】
先在同一直角坐标系中画出函数 、 、 的图象,在不同区间上取靠下的函
数图象,组成函数 的图象,由图象即可观察出函数 的最大值,通过解直线的公共点即
可得此最值.
【详解】
由题意可知 ,函数 的图象如图:联立 ,解得 ,即点 ,
因此,函数 的最大值为 .
故答案为: .
【点睛】
本题主要考查了利用函数图象求函数最值的方法,理解新定义函数的意义,并能画出其图象是解决问题的
关键,属于中等题.
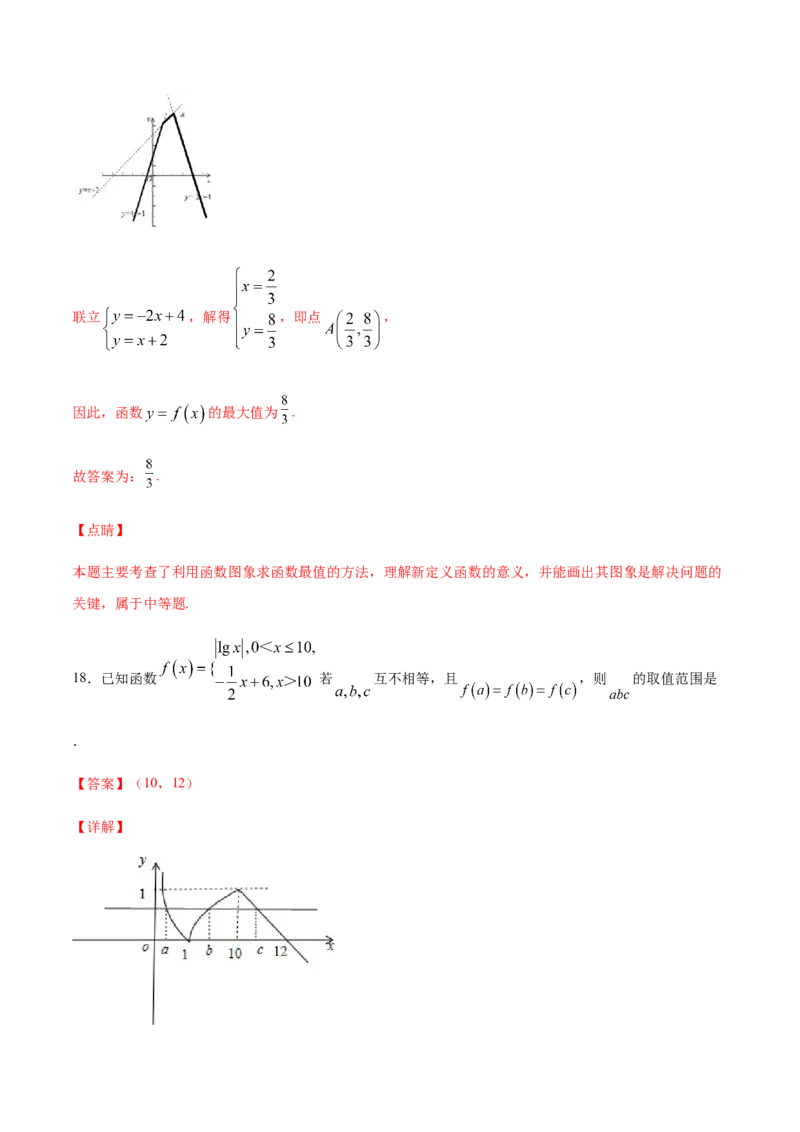
18.已知函数 若 互不相等,且 ,则 的取值范围是
.
【答案】(10,12)
【详解】不妨设a