专题22导数的概念及其意义、导数的运算（原卷版）_E015高中全科试卷_数学试题_选修2_01.同步练习_同步练习（第四套）_高中数学新教材人教A版选择性必修配套提升训练(等10份资料)

专题22 导数的概念及其意义、导数的运算 一、单选题 f(13x) f(1) lim 1．（2020·蚌埠田家炳中学高二开学考试（理））已知 f(1)1，x0 x 等于（ ） 1 A．1 B．-1 C．3 D．3 f(x) x1 2．（2020·黄冈中学第五师分校高二期中（理））设函数 在 处存在导数为2，则 f(1x) f(1) lim  x0 3x （ ）. 2 1 1 A．3 B．6 C．3 D． 2 f xexlnx x1 3．（2020·江西省奉新县第一中学高二月考（理））函数 在 处的切线方程是( ) y ex1 y ex1 y 2ex1 y  xe A． B． C． D． y  xex1 4．（2020·蚌埠田家炳中学高二开学考试（理））曲线 在点（1,1）处切线的斜率等于（ ）. 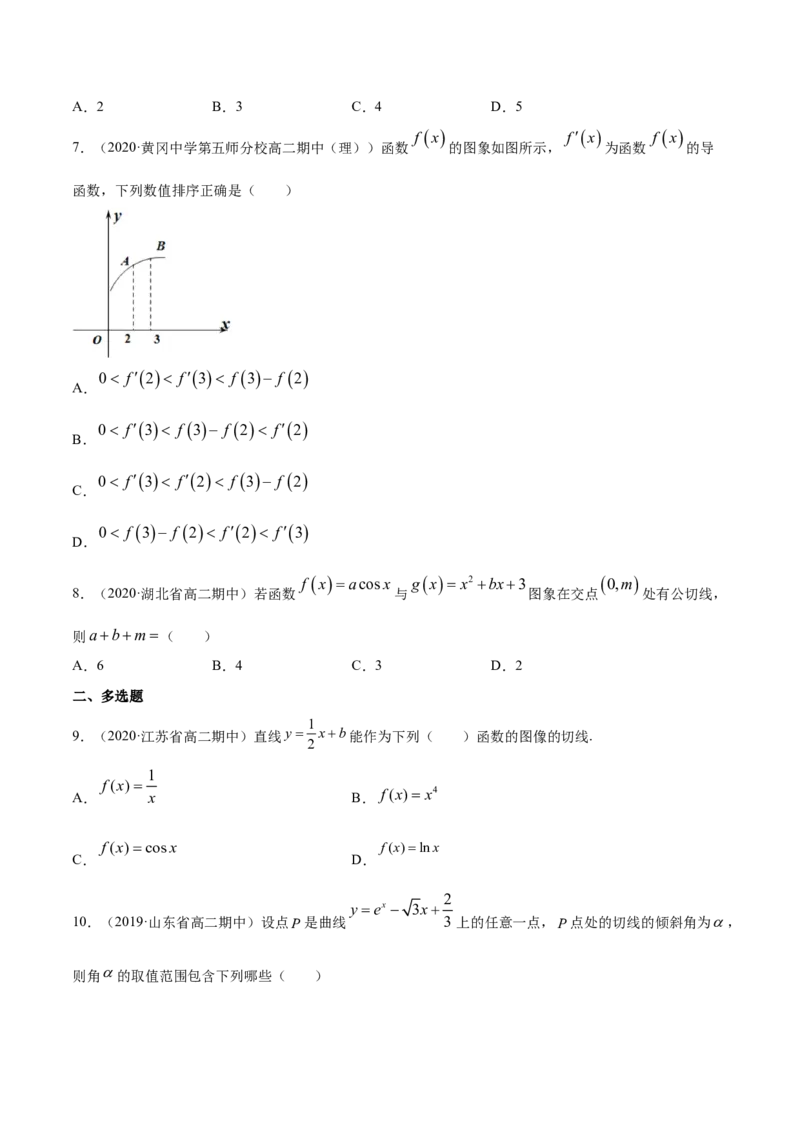2e e A． B． C．2 D．1 f x h f x 3h lim 0 0 5．（2020·江西省奉新县第一中学高二月考（理））若f′(x 0 )＝－3，则 h0 h 等于( ) A．－3 B．－6 C．－9 D．－12 y  f x y  fx x1 6．（2020·江西省奉新县第一中学高二月考（理））已知 的导函数为 ，且在 处 y x3 f 1 f1 的切线方程为 ，则 ( )A．2 B．3 C．4 D．5 f x f x f x 7．（2020·黄冈中学第五师分校高二期中（理））函数 的图象如图所示， 为函数 的导 函数，下列数值排序正确是（ ） 0 f2 f3 f 3 f 2 A． 0 f3 f 3 f 2 f2 B． 0 f3 f2 f 3 f 2 C． 0 f 3 f 2 f2 f3 D． f xacosx gx x2 bx3 0,m 8．（2020·湖北省高二期中）若函数 与 图象在交点 处有公切线， 则abm（ ） A．6 B．4 C．3 D．2 二、多选题 1 9．（2020·江苏省高二期中）直线y xb能作为下列（ ）函数的图像的切线. 2 1 f(x) A． x B． f(x) x4 f(x)cosx f(x)lnx C． D． 2 y ex  3x 10．（2019·山东省高二期中）设点P是曲线 3 上的任意一点，P点处的切线的倾斜角为， 则角的取值范围包含下列哪些（ ）2   5     5  , , 0, 0, ,          A． 3  B．2 6  C． 2 D． 2  6  A(1，2) f xax3 11．（2020·南京市江宁高级中学高二期中）已知点 在函数 的图象上，则过点A的曲线 C: y  f x 的切线方程是（ ） 6x y40 x4y70 A． B． 4x y70 3x2y10 C． D． 1 y  x (x0) 12．（2020·江苏省高二期中）在平面直角坐标系xOy中，点P在曲线 x 上，则点P到直 3x4y20 线 的距离可以为（ ） 4 6 7 A．5 B．1 C．5 D．5 三、填空题 f(x) x34x2 4 (1,1) 13．（2020·江西省石城中学高二月考（文））曲线 在点 处的切线方程为 __________． 14．（2020·横峰中学高二开学考试（文））曲线 y ax1ex 在点 0，1 处的切线的斜率为2，则 a ________． y 4asinxcosx (0,1) y  x1 15．（2020·甘肃省高三二模（文））已知曲线 在点 处的切线方程为 ，  tan(a ) 则 6 ______． 16．（2020·浙江省高三其他）德国数学家莱布尼茨是微积分的创立者之一，他从几何问题出发，引进微积 分概念．在研究切线时，他将切线问题理解为“求一条切线意味着画一条直线连接曲线上距离无穷小的两y  xb f(x)lnx 个点”，这也正是导数定义的内涵之一．现已知直线 是函数 的切线，也是函数 g(x)exk b k  的切线，则实数 ____， _____． 四、解答题 17．（2020·江苏省邗江中学高一期中）求下列函数的导数： (x2)2 f(x) （1） f(x) x2cosx （2） x1 18．（2020·福建省南安市侨光中学高二月考）求下列函数的导数： y  x2(lnxsinx) （1） ； cosxx y  （2） x2 ； y  xlnx （3） . f x x2 xlnx 19．（2020·阳江市第三中学高二月考）已知函数 fx （Ⅰ）求这个函数的导数 ； x1 （Ⅱ）求这个函数在 处的切线方程. f(x) x3 bx2 cxd P(0,2) 20．（2020·定远县育才学校高二月考（理））已知函数 的图象过点 ，且 M(1; f(1)) 6x y70 在点 处的切线方程为 . f(1) f�(-1) （I）求 和 的值. f(x) （II）求函数 的解析式. f(x)2 h(x) 21．（2020·江苏省高二期中）设 f 55， f53，g54，g51， g(x) . h5 h5 （1）求 及 ； y h(x)sin （2）求曲线 6 在x5处的切线方程. b f(x)ax y  f x 22．（2020·攀枝花市第十五中学校高二期中（文））设函数 x ，曲线 在点 (2, f(2)) 3x2y40 处的切线方程为 . f(x) （1）求 的解析式； y  f(x) x0 y  x （2）证明：曲线 上任一点处的切线与直线 和直线 所围成的三角形的面积为定值，并 求此定值.