文档内容
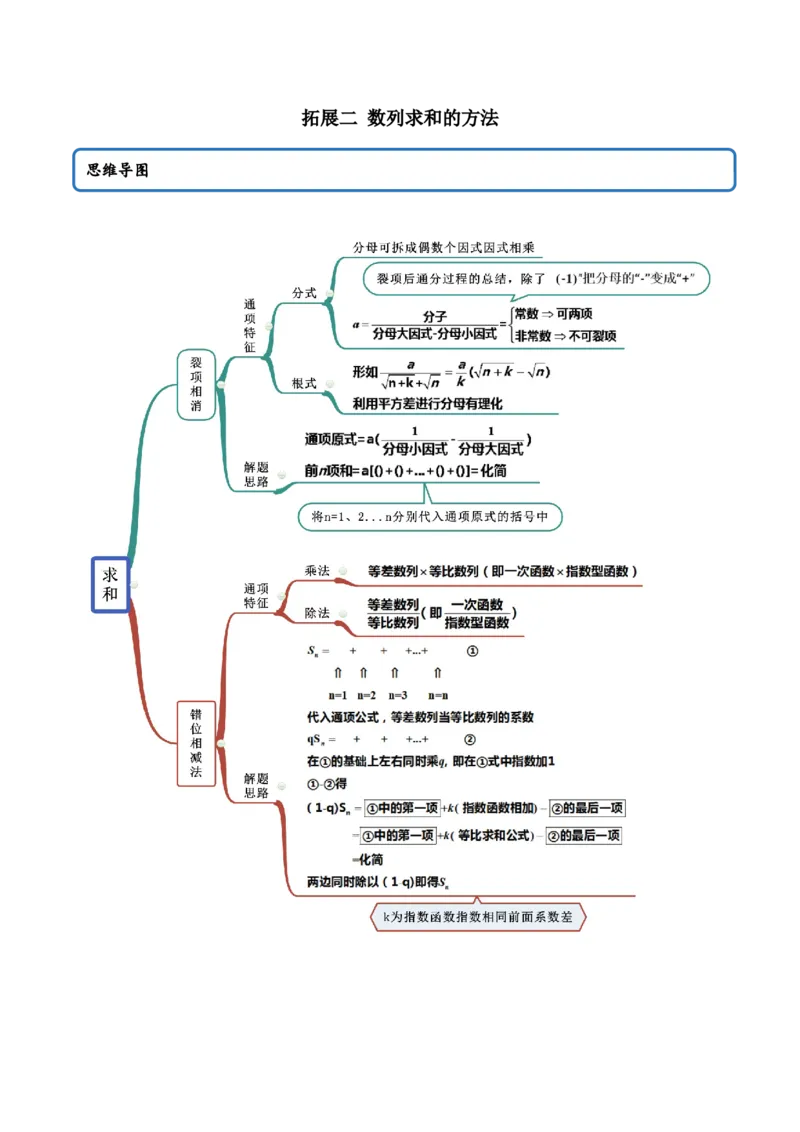
拓展二 数列求和的方法
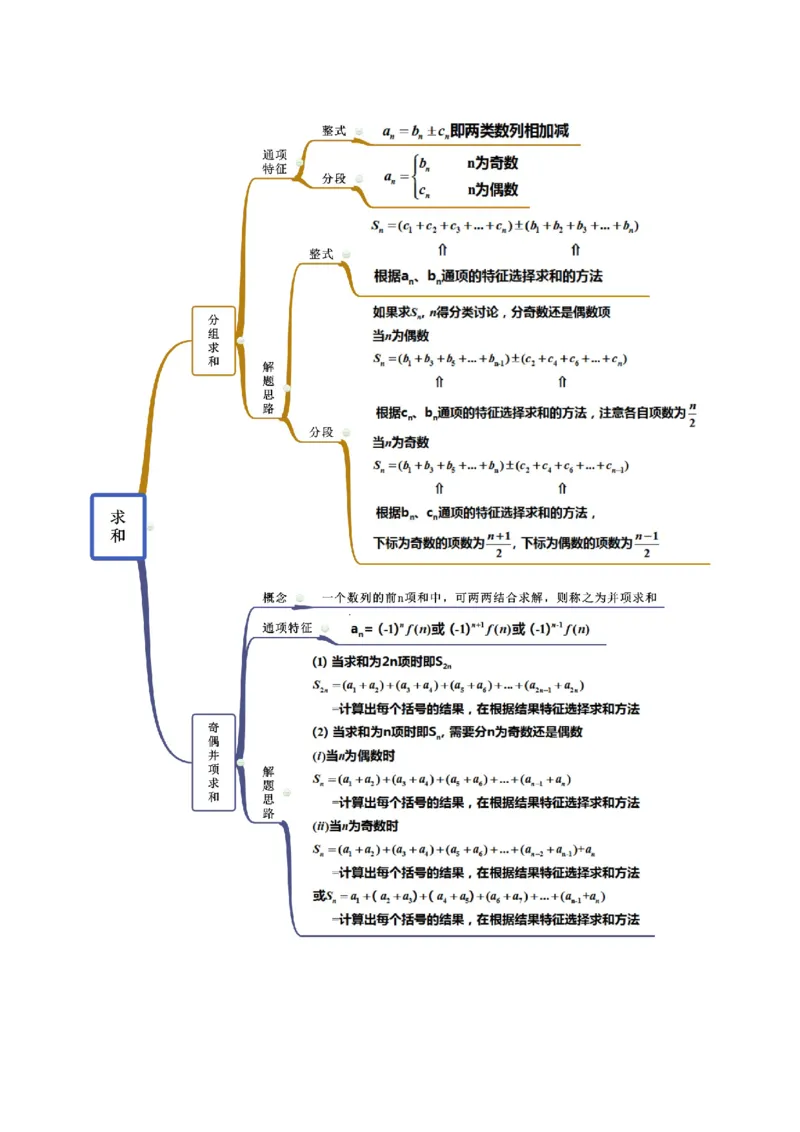
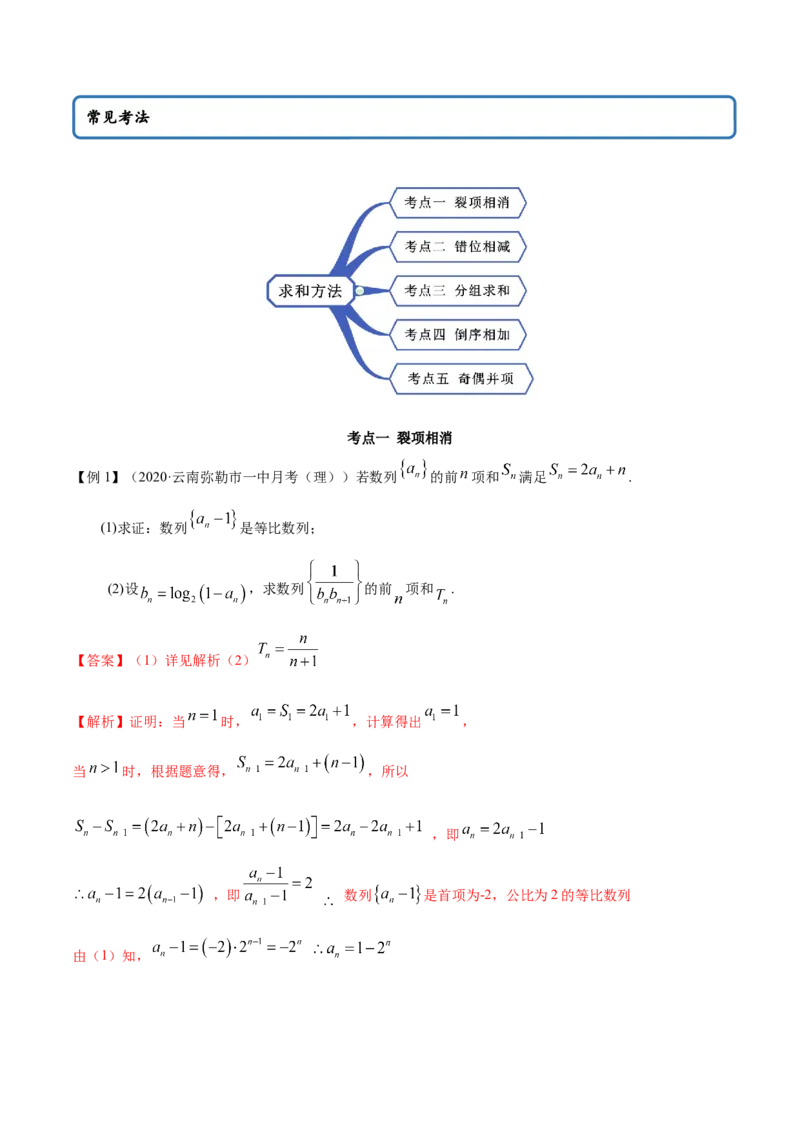
思维导图常见考法
考点一 裂项相消
【例1】(2020·云南弥勒市一中月考(理))若数列 的前 项和 满足 .
(1)求证:数列 是等比数列;
(2)设 ,求数列 的前 项和 .
【答案】(1)详见解析(2)
【解析】证明:当 时, ,计算得出 ,
当 时,根据题意得, ,所以
,即
,即 数列 是首项为-2,公比为2的等比数列
由(1)知,,1
则
【一隅三反】
1.(2020·湖南天心·长郡中学月考(文))设数列 满足: ,且 ( ),
.
(1)求 的通项公式:
(2)求数列 的前 项和.
【答案】(1) ( )(2)
【解析】(1)由 ( )可知数列 是等差数列,设公差为 ,
因为 ,所以 ,解得 ,
所以 的通项公式为: ( );
(2)由(1)知 ,
所以数列 的前 项和:.
2.(2020·石嘴山市第三中学月考)已知 是公差不为零的等差数列, ,且 成等比数列.
(1)求数列 的通项公式;
(2)求数列 的前n项和 .
【答案】(1) ,(2)
【解析】(1)设等差数列 的公差为 ( ),
因为 ,且 成等比数列,
所以 ,即 ,
解得 (舍去)或 ,
所以 ,
(2)由(1)可得 ,
所以
考点二 错位相减
【例2】.(2020·贵州省思南中学月考)已知数列 满足 ,且
(1)求数列 的通项公式;(2)设 ,求数列 的前 项和 .
【答案】(1) ;(2) .
【解析】(1)
时,有 ,即 ,故 ,
又 时也适合该式,
(2)因为 ,
所以 ①
则 ②
①-②得,
.
【一隅三反】
1.(2020·赣榆智贤中学月考)已知数列 是公差 的等差数列,其前n项和为 ,满足
,且 , , 恰为等比数列 的前三项.
(1)求数列 , 的通项公式;
(2)设 ,数列 的前n项和为 ,求证: .
【答案】(1) , ;(2)见解析【解析】(1)由题意, ,得 ,
由 ,得 , .所以 .
由 , ,得公比 ,所以 .
(2)因为 ,所以 ①
得 ②
①-②得
.
所以 .
从而 .
2.(2020·江苏泗阳·桃州中学月考)设数列 、 都有无穷项, 的前 项和为
, 是等比数列, 且 .
(1)求 和 的通项公式;
(2)记 ,求数列 的前 项和为 .【答案】(1) ; (2)
【解析】(1)当 时, = =4;
当 时, ,
且 亦满足此关系,
∴ 的通项为 ,
设 的公比为 ,则 ,则 ,
∴ ;
(2)由题意, ,
而 ,
,
两式相减,有 ,
.
3.(2020·江苏泗阳·桃州中学月考)已知数列 满足 , .
(1)求数列 的通项公式;
(2)求数列 的前 项和 .【答案】(1) ;(2) .
【解析】(1)∵ ,∴ ,而 ,
∴数列 是等比数列,公比为1,首项为1,
∴ ,∴ ;
(2)由(1) ,
设 ,
则 ,
两式相减得 ,∴ ,
∴ .
考点三 分组求和
【例3】.(2020·赣榆智贤中学月考)已知等差数列 的前 项和为 ,等比数列 的前 项和为
.若 , , .
(1)求数列 与 的通项公式;
(2)求数列 的前 项和.
【答案】(1) (2)【解析】(1)由 , ,
则 ,
设等差数列 的公差为 ,则 ,
所以 ,
所以
设等比数列 的公比为
由 ,
,
解得 ,
所以 ,
(2) ,
数列 的前 项和
【一隅三反】
1.(2020·河南高二月考)已知数列 的前 项和 ,在各项均不相等的等差数列 中,
,且 , , 成等比数列,(1)求数列 、 的通项公式;
(2)设 ,求数列 的前 项和 .
【答案】(1) , ;(2) .
【解析】(1)设数列 的公差为 ,则 , ,
∵ , , 成等比数列,∴ ,即 .
整理得 ,解得 (舍去)或 ,
∴ .
当 时, ,当 时, .
验证:当 时, 满足上式,
∴数列 的通项公式为 .
(2)由(1)得, ,
∴
.
2.(2020·河南高二月考(理))已知在等比数列 中, ,且 是 和 的等差中项.
(1)求数列 的通项公式;
(2)若数列 满足 ,求 的前 项和 .
【答案】(1) ;(2) .【解析】(1)设等比数列 的公比为 ,则 ,则 , ,
由于 是 和 的等差中项,即 ,即 ,解得 .
因此,数列 的通项公式为 ;
(2) ,
.
3.(2020·天水市第一中学)已知等比数列 的各项均为正数, , .
(1)求数列 的通项公式;
(2)设 ,求数列 的前n项和 .
【答案】(1) (2)
【解析】(1)设公比为
由题意可知 ,整理得 ,解得 (舍), ,即
则
(2)
考点四 倒序相加
【例4】.(2020·全国高三其他(文))已知函数 ,若,则 的最小值为
( )
A. B. C. D.
【答案】A
【解析】由题可知:
令
又
于是有
因此
所以
当且仅当 时取等号
本题正确选项:
【一隅三反】
1.(2020·江苏高二期中)设函数 ,利用课本(苏教版必修 )中推导等差数列前 项和的
方法,求得 的值为( )
A. B. C. D.
【答案】B【解析】 ,
,
设 ,
则 ,
两式相加得 ,因此, .
故选:B.
2.(2019·浙江丽水·高二月考)已知函数 ,则
的值为( )
A.4033 B.-4033
C.8066 D.-8066
【答案】D
【解析】 ,所以原式
.
3.(2020·江苏常熟中学月考)已知函数 ,设 ( ),则数列 的
前2019项和 的值为( )
A. B. C. D.【答案】A
【解析】因为 ,
所以
所以
因为
所以 ,
所以
则数列 的前2018项和
则
所以
所以
又
故选:
考点五 奇偶并项
【例5】.(2020·湖南高二月考)设 ,数列 的前 项和为 ,已知 ,______.请在① , , 成等比数列,② ,③ ,这三个条件中任选一个补充在上面题干中,
并解答下面问题.
(1)求数列 的通项公式;
(2)若数列 满足 ,求数列 的前 项的和 .
【答案】(1)答案见解析;(2)答案见解析.
【解析】选①,(1)由 得: ,
∴数列 是以 为首项,2为公差的等差数列.
由 , , 成等比数列得 ,解得 .
∴ .
(2) ,
.
选②,(1)由 得 ,
∴数列 是以 为首项,2为公差的等差数列.
由 得 ,解得 ,
∴ .
(2) ,
∴
.选③,(1)同理,由 得 ,
∴数列 是以 为首项,2为公差的等差数列,
由 得 ,解得 ,
∴ .
(2) ,
∴
.
【一隅三反】.
1(2019·广东汕头·金山中学高二月考(理))设 是数列 的前n项和,已知 ,
⑴求数列 的通项公式;
⑵设 ,求数列 的前 项和 .
【答案】(1) (2)
【解析】(1)因为 ,所以当 时,
两式相减得 , 所以
当 时, , ,则所以数列 为首项为 ,公比为 的等比数列, 故
(2)由(1)可得
所以
故当 为奇数时,
当 为偶数时,
综上
2.(2020·内蒙古集宁一中期中(理))已知数列 的前 项和为 .
(1)求数列 的通项公式;
(2)若 ,求数列 的前 项和 .
【答案】(1) ;(2)
【解析】(1)当 时, .
因为 ,所以 ,所以 .
因为 ,所以 .
两式相减,得 ,即又因为 ,所以 .
所以数列 是以 为首项, 为公比的等比数列.
所以 .
(2)由(1)可知
故当 为偶数时,
当 为奇数时,
所以
考点六 绝对值求和
【例6】.(2020·鄂尔多斯市第一中学高二期中(理))已知数列 的通项公式 ,则
( )
A.150 B.162 C.180 D.210
【答案】B
【解析】由对勾函数的性质可知:
当 时,数列 为递减;当 时,数列 为递增.
所以
==
=
=162
【一隅三反】
1.(2020·广东宝安·高二期末)已知 是首项为32的等比数列, 是其前n项和,且 ,则数
列 前10项和为( )
A.58 B.56 C.50 D.45
【答案】A
【解析】 是首项为32的等比数列, 是其前n项和,且 ,所以公比不为1,
,
,
,
,
,
数列 前10项和为 ,
故选:A