文档内容
第二章《一元二次函数、方程和不等式》单元测试 A 卷
(答卷时间:40分钟,满分:100分)
一、单选题(本题共 7 小题,每小题 5 分,共 35 分.在每小题给出的四个选项中,
只有一项符合题目要求)
1.已知 , 则下列结论正确的是 ( )
A. B. C. D.
2.若 ,则 的最小值为 ( )
A.2 B.3 C. D.4
3.不等式 的解集为 ( )
A. B.
C. D.
4.已知 ,则 的最大值为 ( )
A. B. C. D.
5.已知 则 和 的大小关系是 ( )
A. B. C. D.无法确定6.已知不等式 的解集为 ,则 ( )
A. B. C. D.
7.若 ,则函数 取得最小值时 的值为 ( )
A. B. C. D.
二、多选题(本题共 3小题,每小题 5 分,共 15 分.在每小题给出的四个选项中,
有多个选项符合题目要求,完全正确得5分,选对部分得3分,出现错误选项得0
分)
8. 设 为任意两个非零实数,那么“不等式 成立”的一个充分不必要条
件是
A. B. C. D.
9.已知 下列说法一定成立的是 ( )
A. B.
C. D. 的最小值为410.对于任意实数 ,不等式 恒成立,则实数 可以是 ( )
A. B. C. D.
三、填空题(本题共 4小题,每小题 5 分,共 20分,其中14题第一个空2分,第
二个空3分)
11.不等式 的解集是________.
12.已知 则 的最小值是________.
13.设 则“ ”是“ ”的_______________条件.
14.已知 且 和 的算术平均数不小于它们的几何平均数,则此不等关系的表
达式为______________, 时, 的最大值为____________.
四、解答题(本题共 3道大题,每道大题 10分,共 30分.解答应写出必要的文字说
明、证明过程或演算步骤.)
15.解下列一元二次不等式
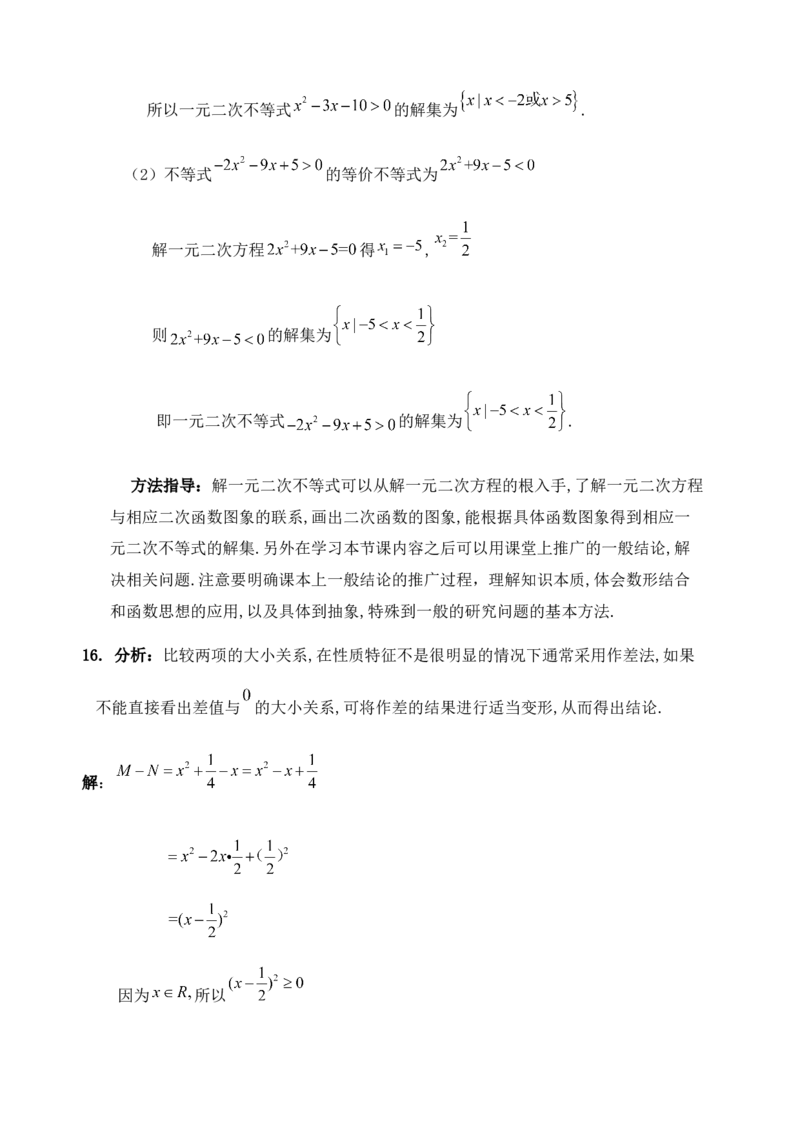
(1) ; (2) .16.已知 ,比较 和 的大小关系,写出详细过程.
17. 若
求证:(1) ;
(2)
第二章《一元二次函数、方程和不等式》单元测试 A 卷参考答案
一、单选题(本题共 7 小题,每小题 5 分,共 35 分.在每小题给出的四个选项中,
只有一项符合题目要求)
1.C.解析:A选项中当 无法判断 的正负所以无法确定 与的大小关系,另外也可以根据不等式的性质中只有满足条件 ,才能得到
因此A错误;B选项中当 时 , 时 ,因此B错误;C
选项中由于 ,不等式两边同时加上同一实数 ,不等号的方向不变(同向可加
性)因此C正确;D选项中由于不清楚实数 的正负,无法通过 得到 和
的大小关系, 故选C.
2.A.解析:基本不等式: 时 ,当且仅当 时等号成立.其中式子
可变形为 .由于 则 ,因此 即 ,
当且仅当 即 时 ,等号成立,所以 的最小值为2, 故选A.(注意
利用基本不等式求最大值或最小值需要满足的条件)
3.A.解析:解一元二次方程 得 , 且二次函数
的图象开口向上,由此该二次函数的图象如图.通过对该函数图象的观察,得到不等
式 的解集为 , 故选A. (注意借助二次函数与一元二次
方程、不等式之间的联系,是求解一元二次不等式的一般性方法).
4.C. 解析:基本不等式: 时 ,当且仅当 时等号成立.变形得.由 可知 , ,则 ,当且仅当
即 时等号成立,所以当 时 有最大值 ,故选C.
5.C. 分析:比较两项的大小关系,在性质特征不是很明显的情况下通常采用作差法,
如果不能直接看出差值与 的大小关系,可将作差的结果进行适当变形,从而得出结
论.
解析: ,所以 ,因此 ,
故选C.
6.D. 解析:因为不等式 的解集为 ,所以1和3是方程
的两个解.
解法一:将 和 分别代入 得 即
解得 所以 ,故选D.
解法二:方程 的两个解1和3,说明方程 是一元二次方程,,则可利用根与系数的关系得到方程组 解得 所以
,故选D.
7.C. 解析: 则 ,所以 ,当且仅
当且仅当 ,即 时 取得最小值4, 所以 取
得最小值时 ,故选C.
二、多选题(本题共 3小题,每小题 5 分,共 15 分.在每小题给出的四个选项中,
有多个选项符合题目要求,完全正确得5分,选对部分得3分,出现错误选项得0
分)
8.AC.思路:题中考查选项中哪几个是“不等式 成立”的充分不必要条件,则该条
件成立时可以推出 ,而当 成立时无法推出该条件成立.本题考查不等式相
关知识,因此注重利用不等式性质及作差法的运用技巧.
解析:A选项,充分性:当 成立时 也成立,因此充分性成立;必要性:当 成立时无法判断 成立,因此必要性不成立.所以 “ ”是“不
等式 成立”的充分不必要条件. B选项,充分性:当 成立时
,由于无法确定 的符号,因此无法确定 是否成立,因此充分性不
成立;必要性:当 成立时 ,由于无法确定 的符号,无法判断
成立,因此必要性不成立.所以 “ ”是“不等式 成立”的既不
充分也不必要条件.C选项,充分性:当 成立时 利用不等式的性质可知
因此 ,即 成立,因此充分性成立;必要性:当 成立时无
法判断 成立,因此必要性不成立.所以 “ ”是“不等式 成立”
的充分不必要条件. D选项,充分性: 当 成立时由于无法确
定 的正负,所以无法确定 和 的大小关系,即无法确定 成立,因此充分性不成立;必要性:同理当 成立时无法确定 成立,因此必要性不成立.
所以 “ ”是“不等式 成立”的既不充分也不必要条件.综上所述可知正
确选项为AC.
9.AB.解析:因为 重要不等式 和基本不等式 均成立,
故A,B正确,当且仅当 时 即 ,所以 不能恒
成立,C错误, 由于 , 则
当且仅当 成立时等号成立,由于 时 无解,所
以 无法取得最小值4,因此D错误. 综上所述可知正确选项为AB.本题
考查对基本不等式的理解及对是否符合利用基本不等式求最值条件的判定能力.
10.ABC. 解析:任意实数 ,不等式 恒成立,则函数 的最小
值 ,解得 ,则选项中满足该条件的实数
可以是 ,故选ABC.
点评:将一元二次不等式恒成立问题转化为函数的最值问题是常见的解题策略,即若 恒成立则只需 ,这一结论是解决这类问题的关键,
也是解决恒成立问题的总的思考方向.
三、填空题(本题共 4小题,每小题 5 分,共 20分,其中14题第一个空2分,第
二个空3分)
11.
解析:本道题考查分式不等式的等价转换.不等式 等价于 ,
解得 ,所以 的解集为 ,注意解集要写成集合或
区间的形式,区间形式将会在下一章学习到.
12.2
解析:本道题考查基本不等式的构造思维能力和对运用基本不等式求最值方法的掌
握. 则 因为 则 ,当且仅当
,即 时等号成立,因此 的最小值为2.
13.必要不充分条件
解析:充分性: ,当 , 时 , ,因此
,充分性不成立; 必要性: 时说明 ,那么一定有 ,,由不等式的性质可知此时 ,即 ,因此
必要性成立.综上所述“ ”是“ ”的必要不充分条件.
14. 第一空: ,第二空:16
解析: 且 和 的算术平均数是 , 和 的几何平均数是 ,因此
“ 和 的算术平均数不小于它们的几何平均数”的符号表达式为 ;由
变形可知 ,当且仅当 时等号成立, ,
,所以当且仅当 时 的最大值16.
四、解答题(本题共 3道大题,每道大题 10分,共 30分.解答应写出必要的文字说
明、证明过程或演算步骤.)
15. 解:(1)解一元二次方程 得 ,
则一元二次函数 的图象如图
y
0所以一元二次不等式 的解集为 .
(2)不等式 的等价不等式为
解一元二次方程 得 ,
则 的解集为
即一元二次不等式 的解集为 .
方法指导:解一元二次不等式可以从解一元二次方程的根入手,了解一元二次方程
与相应二次函数图象的联系,画出二次函数的图象,能根据具体函数图象得到相应一
元二次不等式的解集.另外在学习本节课内容之后可以用课堂上推广的一般结论,解
决相关问题.注意要明确课本上一般结论的推广过程,理解知识本质,体会数形结合
和函数思想的应用,以及具体到抽象,特殊到一般的研究问题的基本方法.
16. 分析:比较两项的大小关系,在性质特征不是很明显的情况下通常采用作差法,如果
不能直接看出差值与 的大小关系,可将作差的结果进行适当变形,从而得出结论.
解:
因为 所以所以 ,即 和 的大小关系是 .
17. 分析:通过观察不难发现两个小问均可采用作差法或利用不等式的性质直接证明.
解:(1) 则
由不等式的性质可知 ,即 ,所以
(2) 则
又